参考文章:
http://blog.csdn.net/u013795055/article/details/38599321
http://blog.csdn.net/g_congratulation/article/details/52734306
感谢以上两位大神让我明白了如何用矩阵快速幂求斐波那契数列。
题外话:线代真的要好好学,这学期刚好学线代,初期还是蛮认真的,可是后来就勉强能听懂,然后慢慢~~。万恶的线代,上学期去湘潭大学参加中南地区程序设计邀请赛第一题就是一个矩阵,三个人都没有学过线代,可那题的通过率还是蛮高的,最终只做了一题打铁的佳绩!
感觉学起来还是蛮简单的,蛮好理解的,以下就我的理解借用大神们一点想法来把矩阵快速幂整理总结!
第一部分:矩阵的基础知识
1.结合性 (AB)C=A(BC).
2.对加法的分配性 (A+B)C=AC+BC,C(A+B)=CA+CB .
3.对数乘的结合性 k(AB)=(kA)B =A(kB).
4.关于转置 (AB)'=B'A'.
一个矩阵就是一个二维数组,为了方便声明多个矩阵,我们一般会将矩阵封装一个类或定义一个矩阵的结构体,我采用的是后者。(弱鸡的我也直只会用结构体实现)
第二部分:矩阵相乘
若A为n×k矩阵,B为k×m矩阵,则它们的乘积AB(有时记做A·B)将是一个n×m矩阵。前一个矩阵的列数应该等于后一个矩阵的行数,得出的矩阵行数等于前一个矩阵的行数,列数等于后一个矩阵的行数。
其乘积矩阵AB的第i行第j列的元素为:

举例:A、B均为3*3的矩阵:C=A*B,下面的代码会涉及到两种运算顺序,第一种就是直接一步到位求,第二种就是每次求一列,比如第一次,C00+=a00*b00,C01+=a00*b01……第二次C00+=a00*b10,C01+=a01*b11……以此类推。。。
C00 = a00*b00 + a01*b10 + a02*b20
C01 = a00*b01 + a01*b11 + a02*b21
C02 = a00*b02 + a01*b12 + a02*b22
C10 = a10*b00 + a11*b10 + a12*b20
C11 = a10*b00 + a11*b11 + a12*b21
C12 = a10*b02 + a11*b12 + a12*b22
C20 = a20*b00 + a21*b10 + a22*b20
C21 = a20*b01 + a21*b11 + a22*b21
C22 = a20*b02 + a21*b12 + a22*b22
C00 = a00*b00 + a01*b10 + a02*b20
C01 = a00*b01 + a01*b11 + a02*b21
C02 = a00*b02 + a01*b12 + a02*b22
下面先来实现一个矩阵相乘的函数吧。
const int MOD=10000;
struct mat
{
int a[2][2];//这里数据范围就用小的示范
};
mat mat_mul(mat x,mat y)//实现两个矩阵相乘,返回的还是一个矩阵。
{
mat res;//用来表示得到的新的矩阵;
memset(res.a,0,sizeof(res.a));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
{
res.a[i][j]+=x.a[i][k]*y.a[k][j];
res.a[i][j]%=MOD;//这一步看题目具体需要了
}
return res;
}学了现代的话这个是很好理解的(个人认为)。
第三部分:矩阵快速幂 //其实和普通快速幂类似,只不过这里需要得到的是一个矩阵
神马是幂?【很多时候会被高大上的名字吓到。。。导致学习效率降低。。。其实没辣么可怕,很简单!!!】
幂又称乘方。表示一个数字乘若干次的形式,如n个a相乘的幂为a^n ,或称a^n为a的n次幂。a称为幂的底数,n称为幂的指数。——引自.度娘百科
这类题,指数都是很大很大很大很大很大很大很大的。。。霸王硬上弓的话,很容易超时的 T_T 。。。所以得快速幂→_→
学过之后发现,其实矩阵快速幂 的核心思想跟 以前学过的快速幂取模非常非常相似,只是矩阵乘法需要另外写个函数,就是上面那个代码。。。
快速幂的思路就是:
设A为矩阵,求A的N次方,N很大,1000000左右吧。。。
先看小一点的,A的9次方
A^9
= A*A*A*A*A*A*A*A*A 【一个一个乘,要乘9次】
= A*(A*A)*(A*A)*(A*A)*(A*A)【保持格式的上下统一,所以加上这句】
= A*(A^2)^4 【A平方后,再四次方,还要乘上剩下的一个A,要乘6次】
= A*((A^2)^2)^2【A平方后,再平方,再平方,还要乘上剩下的一个A,要乘4次】
也算是一种二分思想的应用吧,1000000次幂,暴力要乘1000000次,快速幂就只要(log2底1000000的对数) 次,大约20次。。。这。。。我没错吧。。。
单位矩阵: n*n的矩阵 mat ( i , i )=1; 任何一个矩阵乘以单位矩阵就是它本身 n*单位矩阵=n, 可以把单位矩阵等价为整数1。(单位矩阵用在矩阵快速幂中)
例如下图就是一个7*7的单位矩阵:

下面来实现一个矩阵快速幂:
int pow(int n)//还是小范围数据来说吧,要不然返回值的类型自己定义
{
mat c,res;
memset(res.a,0,sizeof(res.a));
c.a[0][0]=1;//给矩阵赋初值
c.a[0][1]=1;
c.a[1][0]=1;
c.a[1][1]=0;
for(int i=0;i<n;i++) res.a[i][i]=1;//单位矩阵;
while(n)
{
if(n&1) res=mat_mul(res,c);//这里看就要用到上面的矩阵相乘了;
c=mat_mul(c,c);
n=n>>1;
}
return res.a[0][1];
}//时间复杂度log(n)
但是矩阵如何与斐波那契联系在一起呢???
找了很多博客,看了第二位大神的博客才理解。
对于矩阵乘法与递推式之间的关系:
如:在斐波那契数列之中
f[i] = 1*f[i-1]+1*f[i-2] f[i-1] = 1*f[i-1] + 0*f[i-2];
即
所以
给出了矩阵相乘的定义,要你求出斐波那契的第n项对1e4取余。
代码一:在网上看到的很简洁的代码
#include <iostream>
#include <cstddef>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
const int mod=10000;
typedef vector<ll> vec;
typedef vector<vec> mat;
mat mul(mat &a,mat &b)//表示不会这样用,,,,
{
mat c(a.size(),vec(b[0].size()));
for(int i=0; i<2; i++)
{
for(int j=0; j<2; j++)
{
for(int k=0; k<2; k++)
{
c[i][j]+=a[i][k]*b[k][j];
c[i][j]%=mod;
}
}
}
return c;
}
mat pow(mat a,ll n)
{
mat res(a.size(),vec(a.size()));
for(int i=0; i<a.size(); i++)
res[i][i]=1;//单位矩阵;
while(n)
{
if(n&1) res=mul(res,a);
a=mul(a,a);
n/=2;
}
return res;
}
ll solve(ll n)
{
mat a(2,vec(2));
a[0][0]=1;
a[0][1]=1;
a[1][0]=1;
a[1][1]=0;
a=pow(a,n);
return a[0][1];//也可以是a[1][0];
}
int main()
{
ll n;
while(cin>>n&&n!=-1)
{
cout<<solve(n)<<endl;
}
return 0;
}
代码二:自己写的代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD=10000;
struct mat
{
ll a[2][2];
};
mat mat_mul(mat x,mat y)
{
mat res;
memset(res.a,0,sizeof(res.a));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
res.a[i][j]=(res.a[i][j]+x.a[i][k]*y.a[k][j])%MOD;
return res;
}
void mat_pow(int n)
{
mat c,res;
c.a[0][0]=c.a[0][1]=c.a[1][0]=1;
c.a[1][1]=0;
memset(res.a,0,sizeof(res.a));
for(int i=0;i<2;i++) res.a[i][i]=1;
while(n)
{
if(n&1) res=mat_mul(res,c);
c=mat_mul(c,c);
n=n>>1;
}
printf("%I64d\n",res.a[0][1]);
}
int main()
{
int n;
while(~scanf("%d",&n)&&n!=-1)
{
mat_pow(n);
}
return 0;
}
感觉不是很难,裸模板的话没什么问题,但如果灵活度高一点我就不会构造矩阵了。还是继续加油吧!
再次感谢大神们的博客。








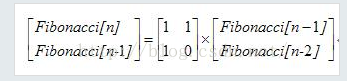
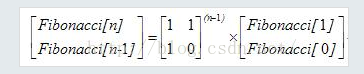














 7736
7736

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








