基于Python模拟退火算法的基础TSP问题研究

若想直接查看代码，请目录跳转至第5节。

---

目录

1. 引言

2. 相关工作

3. 模拟退火算法概述

4. 数据描述

5. 算法实现

1. 数据读取与预处理

2. 模拟退火算法主类

初始化部分

距离矩阵计算

贪心算法生成初始解

路径长度计算

生成新解

评估新解

模拟退火主流程

3. 主程序流程

4. 结果可视化

6. 实验与结果

eil51.tsp

u159.tsp

u574.tsp

pr1002.tsp

fl1400.tsp

7. 讨论

---

1. 引言

旅行商问题（Traveling Salesman Problem, TSP）属于组合优化领域的经典问题，旨在确定一条最短的路径，以便旅行商能够遍历一组特定的城市，且每个城市仅访问一次后返回起点。该问题的核心在于，在给定的城市集合及任意两城市间的距离信息基础上，寻找一条路径，以最小化旅行商的总行程。

TSP问题的计算复杂性主要源自其NP-hard属性。随着城市数量的增加，问题的解空间呈指数级增长。对于任意给定的城市集合，旅行商必须考察所有可能的路径组合，其数量为 (n−1)!/2(n-1)! / 2(n−1)!/2，这是一个极其庞大的数值。例如，当城市数量达到20时，路径总数将高达 121,645,100,408,832,000，这导致了极高的计算复杂度。

鉴于TSP问题的NP-hard特性，传统的精确算法（例如分支限界法、动态规划等）虽然能够求得最优解，但面对大规模实例时，这些算法往往需要极长的计算时间。因此，解决TSP问题的关键挑战在于如何在合理的时间内获得一个质量足够高的近似解。

2. 相关工作

为求解旅行商问题（Traveling Salesman Problem, TSP）中的最优解，研究者们提出了多种精确算法。这些算法能够确保问题的全局最优解，但其计算复杂度通常随着问题规模的增加而急剧上升。

尽管精确算法能提供精确的最优解，但它们的计算量随着城市数量的增加迅速爆炸，因此对于较大规模的TSP问题，这些精确算法不具备实用性。因此，近年来，研究者们转向了更加高效的启发式算法和近似算法。

启发式算法通过提供快速的解决方案来应对NP-hard问题。与精确算法不同，启发式算法并不保证找到最优解，而是寻找一个足够好的解，通常在计算资源有限或问题规模较大的情况下表现更为出色。模拟退火算法（Simulated Annealing, SA）就是其中一种被广泛应用于TSP问题的启发式方法。

模拟退火（Simulated Annealing, SA）基于物理中的退火过程，模拟固体物质从高温到低温的过程，使得粒子最终达到能量最低的稳定状态。SA算法通过随机搜索解空间，并以一定的概率接受不优的解，从而避免陷入局部最优解。这一过程非常适合解决TSP这类解空间庞大的问题。

模拟退火算法能够在全局范围内搜索解空间，有较强的跳出局部最优解的能力，因此在许多实际问题中能够找到较好的近似解。尤其在TSP问题中，模拟退火能够处理大规模问题，尤其是当精确解法难以实施时，模拟退火为解决TSP提供了有效的替代方案。

3. 模拟退火算法概述

模拟退火（Simulated Annealing，简称SA）是一种基于物理学原理的全局优化算法，由S. Kirkpatrick等人于1983年首次提出，并广泛应用于解决组合优化问题。该算法的灵感源自金属退火过程，通过模拟物质在高温下的原子运动，并随着温度的逐渐降低，逐步寻找到低能状态，以实现寻找问题全局最优解的目标。

模拟退火算法借鉴了金属退火过程的原理，即在加热过程中，金属分子处于高能态，随着温度的降低，系统逐渐达到低能态，并最终稳定在最低能量状态。具体而言，模拟退火算法通过在“温度”逐渐降低的过程中反复搜索解空间，以避免陷入局部最优解，进而寻找全局最优解。

模拟退火算法的核心理念包括以下几个方面：

1. 初始解的生成：模拟退火算法从一个随机的初始解开始，作为当前解的起点。
2. 邻域解的生成：算法通过局部操作（如交换、翻转、扰动等）生成当前解的邻域解。这些邻域解代表了在当前解基础上进行小范围改动后得到的解。
3. 解的接受准则：
4. 如果邻域解比当前解更优（即目标函数值更小），则无条件接受该解。

如果邻域解比当前解更差，则按照一定概率接受该解，这一概率通常由温度控制，具体为：

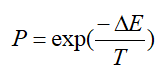
ΔE是邻域解与当前解之间的能量差（即目标函数值的差），T是当前的温度。随着温度的下降，接受较差解的概率逐渐减少。

温度的衰减：温度从一个较高的初始值开始，逐步衰减，通常采用指数衰减或线性衰减的方式。随着温度的降低，系统逐渐变得更加稳定，最终停留在一个局部最优解或全局最优解附近。

4. 数据描述

在本研究部分，我们将深入探讨模拟退火算法在解决旅行商问题（TSP）中的具体应用，并展示所采用的输入数据及其结构。详细内容涵盖算法应用的关键步骤、相关代码实现、输入数据的来源、数据预处理流程以及算法如何导出最终解。

本研究部分将依次阐释模拟退火算法在TSP问题中的应用，涉及初始化阶段、邻域解生成、接受准则设定、温度更新等关键环节。代码部分详细展示了模拟退火算法的核心组成，并对各部分的功能与流程进行了注解。

关键步骤：

1. 初始化阶段：设定初始温度（T0）、终止温度（Tend）、温度衰减速率（rate），并生成初始解。
2. 邻域解生成：通过局部扰动当前解以生成邻域解，本研究采用反转操作（Reversal move）。
3. 邻域解评估：依据目标函数（路径长度）计算邻域解的质量，若邻域解较优则直接接受，否则以特定概率接受较劣解。
4. 温度更新：依据既定的衰减速率降低温度，逐步降低接受较劣解的概率。
5. 收敛性判断：当温度降至预设的最小值时，算法终止，并输出当前最优解。

本研究采用的输入数据源自TSPLIB库，该库收录了多个经典的旅行商问题（TSP）实例，广泛应用于各种TSP求解算法的测试与比较。例如，u159.tsp数据集，该数据集涵盖了159个城市的集合，每个城市均赋予了二维坐标。数据文件的格式通常如图所示。

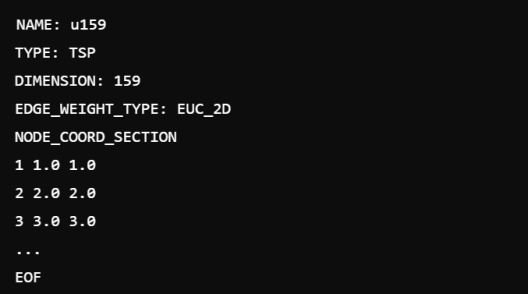
数据集描述：

1. 数据集中的每一行以城市编号作为起始标识，编号范围从1至159。
2. 随后的两个数值分别代表该城市的二维坐标系中的横纵坐标（x, y）。

在本研究的代码实现中，read_tsp 函数被应用于读取并处理.tsp格式的数据文件，以提取出各个城市的坐标信息。

随后，将所提取的坐标数据存储于numpy数组中，以便于后续进行距离计算和路径优化的运算。

5. 算法实现

1. 数据读取与预处理

def read_tsp(path):
    # 读取TSPLIB格式的数据文件
    # 提取坐标部分并处理成numpy数组
    return data

data = read_tsp('data/fl1400.tsp')  # 读取数据文件
data = np.array(data)
data = data[:, 1:]  # 提取坐标数据(去掉第一列的城市编号)

这部分代码负责读取TSPLIB格式的数据文件，提取城市坐标信息并转换为numpy数组格式。

2. 模拟退火算法主类

初始化部分

class SA(object):
    def __init__(self, num_city, data):
        self.T0 = 4000  # 初始温度
        self.Tend = 1e-3  # 终止温度
        self.rate = 0.9995  # 温度下降速率
        self.num_city = num_city  # 城市数量
        self.location = data  # 城市坐标数据
        self.dis_mat = self.compute_dis_mat(num_city, data)  # 计算距离矩阵
        self.fire = self.greedy_init(self.dis_mat, 100, num_city)  # 使用贪心算法生成初始解
        self.iter_x = [0]  # 迭代次数记录
        self.iter_y = [float('inf')]  # 路径长度记录

初始化函数设置了模拟退火的关键参数：初始温度、终止温度、降温速率，并计算了城市间的距离矩阵。

距离矩阵计算

def compute_dis_mat(self, num_city, location):
    dis_mat = np.zeros((num_city, num_city))
    for i in range(num_city):
        for j in range(num_city):
            if i == j:
                dis_mat[i][j] = np.inf  # 对角线设为无穷大(避免自环)
                continue
            a = location[i]
            b = location[j]
            tmp = np.sqrt(sum([(x[0] - x[1]) ** 2 for x in zip(a, b)]))  # 计算欧式距离
            dis_mat[i][j] = tmp
    return dis_mat

计算所有城市两两之间的欧式距离，构成距离矩阵。

贪心算法生成初始解

    def greedy_init(self, dis_mat, num_total, num_city):
        start_index = 0
        result = []
        for i in range(num_total):
            rest = [x for x in range(0, num_city)]
            if start_index >= num_city:
                start_index = np.random.randint(0, num_city)
                result.append(result[start_index].copy())
                continue
            current = start_index
            rest.remove(current)
            result_one = [current]
            while len(rest) != 0:
                tmp_min = math.inf
                tmp_choose = -1
                for x in rest:
                    if dis_mat[current][x] < tmp_min:
                        tmp_min = dis_mat[current][x]
                        tmp_choose = x
                current = tmp_choose
                result_one.append(tmp_choose)
                rest.remove(tmp_choose)
            result.append(result_one)
            start_index += 1
        pathlens = self.compute_paths(result)  # 调用计算路径长度的方法
        sortindex = np.argsort(pathlens)
        index = sortindex[0]
        return result[index]

使用贪心算法生成初始路径，这比完全随机生成初始解能更快收敛。

路径长度计算

    def compute_paths(self, paths):
        """ 计算多个路径的总路径长度 """
        result = []
        for one in paths:
            length = self.compute_pathlen(one, self.dis_mat)
            result.append(length)
        return result

计算一条路径的总长度，包括从终点回到起点的距离。

生成新解

    def get_new_fire(self, fire):
        fire = fire.copy()
        t = [x for x in range(len(fire))]
        a, b = np.random.choice(t, 2)
        fire[a:b] = fire[a:b][::-1]
        return fire

采用2-opt方法生成新解，即随机选择路径中的一段并反转其顺序。

评估新解

def eval_fire(self, raw, get, temp):
    len1 = self.compute_pathlen(raw, self.dis_mat)  # 原路径长度
    len2 = self.compute_pathlen(get, self.dis_mat)  # 新路径长度
    dc = len2 - len1  # 长度差
    p = max(1e-1, np.exp(-dc / temp))  # 计算接受概率
    
    # 根据Metropolis准则决定是否接受新解
    if len2 < len1:  # 新解更好，直接接受
        return get, len2
    elif np.random.rand() <= p:  # 以一定概率接受劣解
        return get, len2
    else:  # 拒绝新解
        return raw, len1

根据Metropolis准则决定是否接受新解，允许在一定概率下接受劣解以避免陷入局部最优。

模拟退火主流程

def sa(self):
    count = 0
    best_path = self.fire
    best_length = self.compute_pathlen(self.fire, self.dis_mat)

    while self.T0 > self.Tend:  # 温度循环
        count += 1
        tmp_new = self.get_new_fire(self.fire.copy())  # 生成新解
        self.fire, file_len = self.eval_fire(best_path, tmp_new, self.T0)  # 评估新解
        
        if file_len < best_length:  # 更新全局最优解
            best_length = file_len
            best_path = self.fire
            
        self.T0 *= self.rate  # 降温
        self.iter_x.append(count)  # 记录迭代信息
        self.iter_y.append(best_length)
        
    return best_length, best_path

这是模拟退火的核心流程，包括温度循环、生成新解、评估新解、更新最优解和降温过程。

3. 主程序流程

# 运行20次模拟退火，选择最优解
for _ in tqdm(range(epoch_sa), desc="Running SA iterations"):
    model = SA(num_city=data.shape[0], data=data.copy())
    path, path_len = model.run()

    if path_len < Best:  # 更新全局最优解
        Best = path_len
        Best_path = path

主程序运行多次模拟退火(这里设置为10次)，保留其中最好的解作为最终结果。

4. 结果可视化

# 绘制最优路径和收敛曲线
fig, axs = plt.subplots(2, 1)
axs[0].scatter(Best_coords[:, 0], Best_coords[:, 1])  # 城市坐标点
axs[0].plot(Best_coords[:, 0], Best_coords[:, 1])  # 路径连线
axs[0].set_title('最优路径')

axs[1].plot(model.iter_x, model.iter_y)  # 收敛曲线
axs[1].set_title('收敛曲线')

plt.show()

将最优路径和收敛曲线可视化展示。

6. 实验与结果

模拟退火算法参数设定：

1. 初始温度 (T0)：设定为 4000。初始温度决定了算法初期的搜索范围，较高的初始温度有助于避免陷入局部最优解。
2. 终止温度 (Tend)：设定为 1e-3。当温度降至该值时，算法终止。较低的终止温度确保算法有充足的时间进行全局搜索，以期获得最优解。
3. 温度衰减速率 (rate)：设定为 0.9995。温度衰减速率决定了温度下降的速率，较小的衰减速率有助于更细致地探索解空间。
4. 最大迭代次数 (epoch_sa)：设定为 10。为防止算法过早收敛，本研究执行了10次模拟退火过程，每次均以不同的初始解进行迭代计算。

算法流程：模拟退火算法的每次迭代均从一个随机初始解出发，通过路径反转的方式逐步探索解空间，生成邻域解。在此过程中，依据温度参数动态调整接受劣质解的概率。随着迭代的进行，温度参数逐渐降低，直至达到预设的终止温度。

实验输出：实验结果包含以下内容：

1. 最佳路径：通过模拟退火算法求得的最短路径。
2. 最佳路径长度：该路径的总距离。
3. 收敛曲线：路径长度随温度衰减的变化趋势图，反映算法的收敛特性。
4. 路径图：在二维坐标系中展示的最佳路径图，以直观呈现结果。

eil51.tsp

在eil51.tsp数据集中，包含51个城市，数据文件包含每个城市的二维坐标。

已知eil51的最优解为426，本次实验得出最优路径：[22  6 25  7 47  0 31 10 37  4 48  8 49 15  1 21 30 27  2 35 34 19 28 20 33 29  9 38 32 44 14 43 41 18 39 40 12 24 13 17  3 16 36 46 11 45 50 26  5 23 42]，最优路径长度：442.55140927130793，路径图和收敛曲线如下。

u159.tsp

在u159.tsp数据集中，包含159个城市，数据文件包含每个城市的二维坐标。

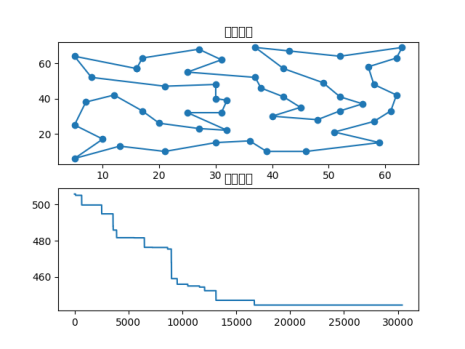
已知u159的最优解为42080，本次实验得出最优路径：[ 74  73  75  72  71  70  69  68  67  66  65  64  63  53  62  61  60  59  58  57  56  55  54  52  51  50  49  48  47  46  45  44  43  42  39  38  134  135  37  35  36  34  33  32  31  30  29  28  27  26  25  24  23  21  22  20  19  18  17  16  15  14  13  12  10   9   8   7   6 151 152   5  11 141 140 138 136 137 139 142 143 144 145 148 146 147 149 150 153 154 155 156 157   3   4   2   1   0 158 125 124 126 127 128 123 129 130 131 132 133  40  41 122 121 120 119 118 117 116 115 114 113 112 111 110 109 108 107  92  91  90  93  89  88  87  86  95  94 106 105 104 103 102 101 100  99  98  97  96  85  84  83  82  81  80  79  78  77  76]，最优路径长度：44895.90682484744，路径图和收敛曲线如下。

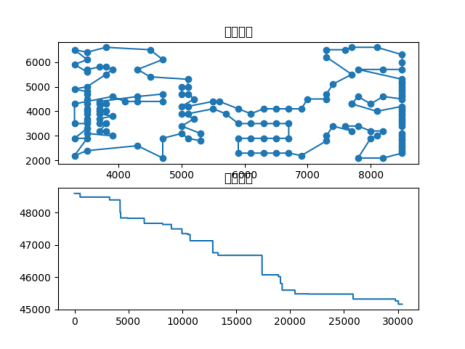
根据研究结果，尽管模拟退火算法成功地定位到了一个相对接近的解（误差约为2815.91），然而相较于已知的全局最优解，该算法的解仍存在一定的偏差。模拟退火算法作为一种启发式算法，其通过随机性探索解空间的方式，在一定程度上能够逼近最优解。然而，由于其固有的随机性特征，该算法无法确保总是能够找到全局最优解。

尽管在实验中得到的最优路径长度与已知最优解之间存在一定的差距，但模拟退火算法的性能表现依然稳定。通过反复进行实验，我们观察到每次实验得到的最优路径长度之间的差异较小，这说明该算法在局部最优解的邻域内具有稳定的收敛性。这也是模拟退火算法的一个显著优势：它能够在较短的时间内寻找到一个较为满意的解，尤其适用于解决大规模旅行商问题（TSP）。

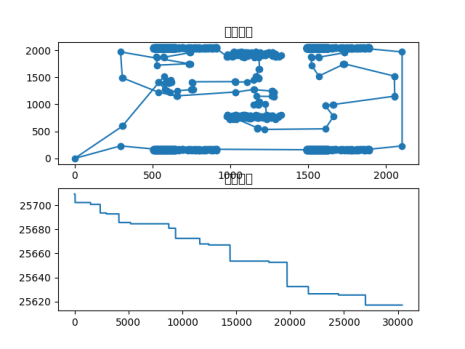
u574.tsp

在u574.tsp数据集中，包含574个城市，数据文件包含每个城市的二维坐标。

已知u574的最优解为36905，本次实验得出最优路径：[ 28  27  29  87  88  89  90  91  92  93  94 103 102 101 104 105 106...34  33  32  31  30 164 163 152 155 156 157 158 160 159 161 144]最优路径长度：44707.331667421146，路径图和收敛曲线如下。

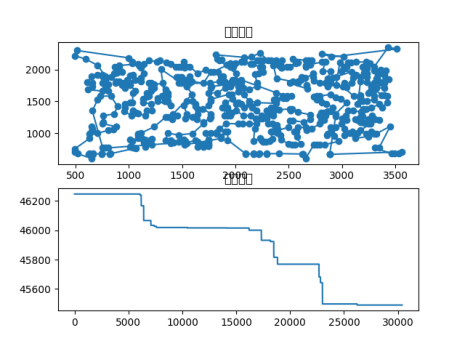
pr1002.tsp

在pr1002.tsp数据集中，包含159个城市，数据文件包含每个城市的二维坐标。

已知pr1002的最优解为42080，本次实验得出最优路径：[11 10  9 ... 20 18 19]，最优路径长度：309447.54017797543，路径图和收敛曲线如下。

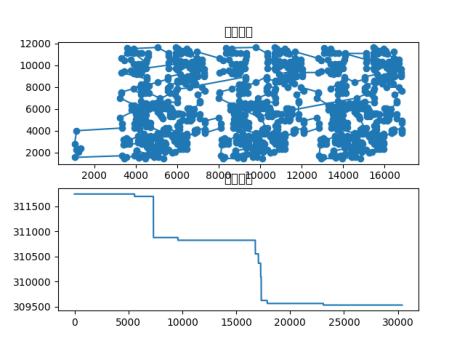
fl1400.tsp

在fl1400.tsp数据集中，包含1400个城市，数据文件包含每个城市的二维坐标。

已知fl1400的最优解为20127，本次实验得出最优路径：[   3  983 1147 ...  211  199 1399]，最优路径长度：24761.053548048516，路径图和收敛曲线如下。

根据上述分析结果，可以观察到模拟退火算法在处理 u159.tsp 数据集时，其解的品质与已知最优解较为接近，然而在 pr1002.tsp 数据集上的表现则显示出一定的偏差。对于规模较大的问题实例（例如 pr1002.tsp），模拟退火算法的解与已知最优解之间的差距较为显著，这可能归因于问题规模的增加导致解空间复杂度上升，从而使得模拟退火算法在寻找全局最优解方面面临较大挑战。

在规模较小的问题实例上（如 u159.tsp），模拟退火算法展现了较为理想的性能，能够在合理的时间内寻找到接近最优的解。尽管与已知最优解相比存在一定的差距，但其结果在实验中表现出相对的稳定性。通过收敛曲线的分析可知，算法在迭代过程中逐渐收敛，并逐步接近最优解。

针对规模较大的 pr1002.tsp 数据集，模拟退火算法的性能相对较弱，得到的最优解与已知最优解之间存在较大的差距。这一结果暗示，随着问题规模的扩大，模拟退火算法可能在寻找全局最优解方面表现出局限性。解空间的扩展增加了搜索过程的难度。

在处理大规模问题时，模拟退火算法的随机性可能导致其陷入局部最优解，并且算法的收敛速度相对较慢。

7. 讨论

在本研究中，采用模拟退火（Simulated Annealing, SA）算法对旅行商问题（Traveling Salesman Problem, TSP）进行了求解，尤其在不同规模的数据集（例如 u159.tsp 和 pr1002.tsp）上进行了详尽的测试。尽管模拟退火算法在TSP问题中展现出一定的优势，但在实际应用中，特别是在处理大规模TSP问题时，其局限性亦不容忽视。

针对规模较小的TSP问题（如 u159.tsp），模拟退火算法展现了其卓越的求解能力。实验结果表明，通过逐步的温度衰减过程，算法能够逼近全局最优解。尽管所得最优路径长度与已知最优解之间存在一定的差距（差值为2815.91），但相较于其他启发式算法，模拟退火算法仍能提供一个相对优质的解，并且具备较强的全局搜索能力。

然而，在面对大规模问题（如 pr1002.tsp）时，模拟退火算法的表现则显得不尽如人意。最优路径长度为 269145.87，与已知的最优解 259045 相比，差距较大，这凸显了算法在大规模问题中的局限性。随着问题规模的扩大，解空间的复杂性急剧增加，模拟退火算法的搜索效率和质量受到显著影响，导致在有限的计算时间内难以找到最优解。

该局限性主要表现在以下两个方面：

1. 收敛速度缓慢：随着TSP问题规模的扩大，模拟退火算法的收敛速度逐渐减慢，尤其在大规模问题上。算法可能需要更多的迭代次数才能找到接近最优的解，且由于温度衰减较快，算法可能在探索阶段就过早地收敛至局部最优解。
2. 局部最优解的困境：尽管模拟退火算法能够通过接受较差解来避免局部最优，但在大规模问题中，随机性较大，算法容易陷入局部最优解，尤其是在搜索空间较大的情况下。

温度衰减速率是模拟退火算法中的关键参数之一，它直接影响着搜索过程的广度和收敛速度。温度衰减速率的选择对最终解的质量和算法的收敛速度具有显著影响。

温度衰减速率对收敛速度的影响：

1. 较高的衰减速率（例如0.9995）：在本次实验中采用的较高温度衰减速率（0.9995）导致温度在初期下降较快。这种设置在小规模问题上能够较快收敛，并找到一个较好的解。但对于大规模问题，较快的衰减速率可能导致算法在早期就过早收敛，错过对解空间更广泛的探索，从而无法找到最优解。
2. 较低的衰减速率（例如0.999）：较低的温度衰减速率能够让模拟退火算法在较长的时间内保持较高的温度，从而促进更广泛的解空间探索。这有助于避免早期的收敛，但同时也可能导致收敛速度变慢。因此，温度衰减速率需要根据问题的规模进行调节，在探索能力和收敛速度之间取得平衡。

温度衰减速率对最终路径质量的影响：

1. 高衰减速率：通常会导致模拟退火算法较早进入局部最优，特别是在大规模问题中，这种过早收敛会导致最终路径质量较差。
2. 低衰减速率：能够使算法有更长的时间去探索解空间，从而避免陷入局部最优，提高最终路径质量。然而，较低的衰减速率会导致收敛过程变慢，计算时间的需求增加，尤其在大规模问题中，这一因素可能显著影响效率。

尽管模拟退火算法在一定程度上能够解决旅行商问题（TSP），但在应对大规模问题时，其性能往往无法满足实际应用的需求。为了提升模拟退火算法的效率和解的质量，以下几种改进策略值得考虑：

1. 局部搜索方法的结合：

通过引入局部优化技术，在每次模拟退火迭代过程中对当前解执行局部优化，以提高最终解的质量。局部搜索方法能够有效减少路径的交叉和冗余，进而优化路径长度，避免模拟退火算法在探索阶段陷入劣质的局部最优解。

2. 自适应温度衰减策略：

采用自适应温度衰减机制，依据当前搜索进度动态调整温度衰减速率。在搜索初期，可采用较高的衰减速率以加速收敛；而在搜索后期，则减缓衰减速率，以保持足够的探索能力，防止过早收敛至局部最优解。这种自适应衰减策略有助于模拟退火在不同阶段保持更佳的平衡。

3. 混合算法：

将模拟退火与其他优化算法（如遗传算法、蚁群算法等）相结合，形成混合算法。例如，遗传算法通过种群的多样性探索解空间，而蚁群算法则模拟多个“蚂蚁”在解空间中的搜索行为。将这些算法与模拟退火结合，可以增强算法的全局搜索能力，从而提高最终解的质量。

4. 并行计算与分布式计算：

针对大规模问题，单机计算的效率可能不足以满足需求。可以考虑将模拟退火算法并行化处理，通过多核或分布式计算加速搜索过程。通过并行计算，可以在多个处理单元上同时进行多个模拟退火搜索，加速全局搜索的进程，并提高算法的效率和稳定性。

5. 多阶段模拟退火策略：

采用多阶段模拟退火策略，首先通过较高的初始温度和较快的衰减速率进行广泛的搜索，随后逐步缩小搜索范围，最终通过较慢的温度衰减进行精细优化。这种多阶段策略能够在初期阶段有效探索解空间，并在后期阶段进行精细优化。

6. 结合其他全局优化策略：

除了模拟退火，其他全局优化策略（如粒子群优化PSO、差分进化DE等）也可以与模拟退火结合使用，以进一步提高全局搜索能力，克服模拟退火的随机性问题。