正文### 1、一个齐次线性方程组的所有解,形成一个向量空间
对于一个齐次线性方程组 A x = O Ax= O Ax=O来说,它的所有的解中每一解都是向量,那么把这些向量(齐次线性方程组的解)集合在一起形成一个空间,其实这个空间是一个向量空间。
这个结论可以证明如下:
对于一个齐次线性方程组
A
x
=
O
Ax= O
Ax=O,它一定有解,因为至少会存在一个零解,所以它的所有解形成的空间不可能为空。
C a s e 1 Case \ 1 Case 1 当这个齐次线性方程组只有唯一零解 的时候,意味着它的解形成的空间只有一个零向量,此时这个空间的维度为 0 0 0,空间内向量的加法和数量乘法满足封闭性,是一个向量空间,很容易得证。
C
a
s
e
2
Case \ 2
Case 2当这个齐次线性方程组有无数解 的时候,求证它的解形成的空间是向量空间:
假设这个齐次线性系统的系数矩阵
A
A
A是一个
m
∗
n
m*n
m∗n的矩阵,那么它的每个解都是一个
n
n
n维向量(有序实数元组)。如果这些解形成的空间是向量空间,则一定是
n
n
n维空间(
欧几里得空间
R
n
\color {darkred} {\small \textbf{ 欧几里得空间}} \ \ \ R^{n}
欧几里得空间 Rn是向量空间)的子空间。

所以当证明齐次线性方程组的解形成的空间是
n
n
n维欧几里得空间的子空间,就说明它是一个向量空间。
只需证明这个空间对向量加法和数量乘法封闭
\color {darkred} {只需证明这个空间对向量加法和数量乘法封闭}
只需证明这个空间对向量加法和数量乘法封闭
(1)证明空间对向量加法封闭
假设向量 u ⃗ \vec u u和 v ⃗ \vec v v是齐次线性方程组 A x = O Ax= O Ax=O的两个解
就有 A ⋅ u ⃗ = O , A ⋅ v ⃗ = O → A ⋅ u ⃗ + A ⋅ v ⃗ = O A \cdot \vec u = O, \ A \cdot \vec v = O \to A \cdot \vec u + A \cdot \vec v = O A⋅u=O, A⋅v=O→A⋅u+A⋅v=O ;
进而可得 A ⋅ ( u ⃗ + v ⃗ ) = O A \cdot (\vec u + \vec v) = O A⋅(u+v)=O;
上式子意味着两向量 u ⃗ \vec u u, v ⃗ \vec v v的和 ( u ⃗ + v ⃗ ) (\vec u + \vec v) (u+v)也是这个齐次线性方程组的解;
因此对于齐次线性方程组的解形成的空间内任意取两个向量 u ⃗ \vec u u和 v ⃗ \vec v v, u ⃗ + v ⃗ \vec u + \vec v u+v还是在这个空间内,所以该空间对向量加法封闭
(2)证明空间对向量的数量乘法封闭
假设向量 u ⃗ \vec u u是齐次线性方程组 A x = O Ax= O Ax=O的一个解
就有 A ⋅ u ⃗ = O A \cdot \vec u = O A⋅u=O, 这个等式两边同乘以一个实数 k k k,可得 k ⋅ A ⋅ ( u ⃗ + v ⃗ ) = k ⋅ O = O k \cdot A \cdot (\vec u + \vec v) = k \cdot O = O k⋅A⋅(u+v)=k⋅O=O;
改写后可得 A ⋅ ( k u ⃗ ) = O A \cdot (k \vec u) = O A⋅(ku)=O;
上式子意味着向量 k u ⃗ k\vec u ku也是这个齐次线性方程组的解;
因此对于齐次线性方程组的解形成的空间内任意取一个向量 u ⃗ \vec u u,那么这个 u ⃗ \vec u u乘以任何一个实数 k k k,结果 k u ⃗ k\vec u ku还是在这个齐次线性方程组的解形成的空间内,所以该空间对数量乘法封闭。
>>综上,一个齐次线性方程组的所有解,形成一个向量空间得证
2、矩阵的零空间
零空间 \color{red} { 零空间} 零空间:一个齐次线性方程组的所有解,形成一个向量空间,称这个空间为" 零空间 ( N u l l S p a c e ) \color{red} {\small 零空间 (Null \ Space)} 零空间(Null Space)"。
对于一个矩阵 A A A来说,它的零空间就是以 A A A为系数矩阵的齐次线性方程组 A x = 0 Ax=0 Ax=0中,这个线性系统所有的解 x x x组成的空间就是矩阵 A A A的零空间。
零空间 \color{red} { 零空间} 零空间是矩阵的一个特殊的子空间,矩阵的零空间相比矩阵的行空间和列列空间要更加抽象,因为对于一个矩阵的行空间和列空间,我们可以直观的看到生成它们的就是这个矩阵的行向量和列向量,然后因为这些行向量和列向量可能线性相关,所以往往需要通过特殊的计算手段(对矩阵进行高斯消元求算矩阵的秩)来获得行空间和列空间的具体维度,进而能找到空间的一组基。相比之下,生成一个矩阵的零空间的向量,需要通过求解齐次线性方程组 A x = 0 Ax=0 Ax=0来获取。
对零空间的一些理解
对于线性系统 A x = O Ax=O Ax=O,所有的 x x x组成的空间是零空间。
-
如果把矩阵看成是向量的转换函数,那么对于等式 A x = O Ax=O Ax=O,其中系数矩阵A就可以看成是一个转换函数,零空间是一个集合,集合内的所有向量在A的变换下,都可以被映射到零点!
-
如果把矩阵看成是空间,那么就有零空间内任意向量和矩阵 A A A的行向量的点乘结果为0!
进一步推广,因为矩阵 A A A的行空间内的任意向量都由矩阵的行向量的线性组合所表示(如 w ⃗ = k 1 u ⃗ + k 2 v ⃗ \vec w = k_1 \vec u + k_2 \vec v w=k1u+k2v),而零空间内任意向量和矩阵 A A A的行向量的点乘结果为 0 0 0,就有 x ⃗ ⋅ w ⃗ = k 1 u ⃗ ⋅ x ⃗ + k 2 v ⃗ ⋅ x ⃗ = 0 \vec x \cdot \vec w = k_1 \vec u \cdot \vec x + k_2 \vec v \cdot \vec x = 0 x⋅w=k1u⋅x+k2v⋅x=0,所以可以得出结论"对于零空间内的任意向量,和矩阵 A A A的行空间的任意向量的点乘结果为 0 0 0" 这个结论其实表面,零空间内的所有向量,和矩阵 A 的行空间中的所有向量是垂直 ( 正交 ) 的。 → \color {#0088b9} {\small {这个结论其实表面,零空间内的所有向量,和矩阵A的行空间中的所有向量是垂直(正交)的。}} \to 这个结论其实表面,零空间内的所有向量,和矩阵A的行空间中的所有向量是垂直(正交)的。→ 矩阵A的零空间与矩阵A的行空间正交。
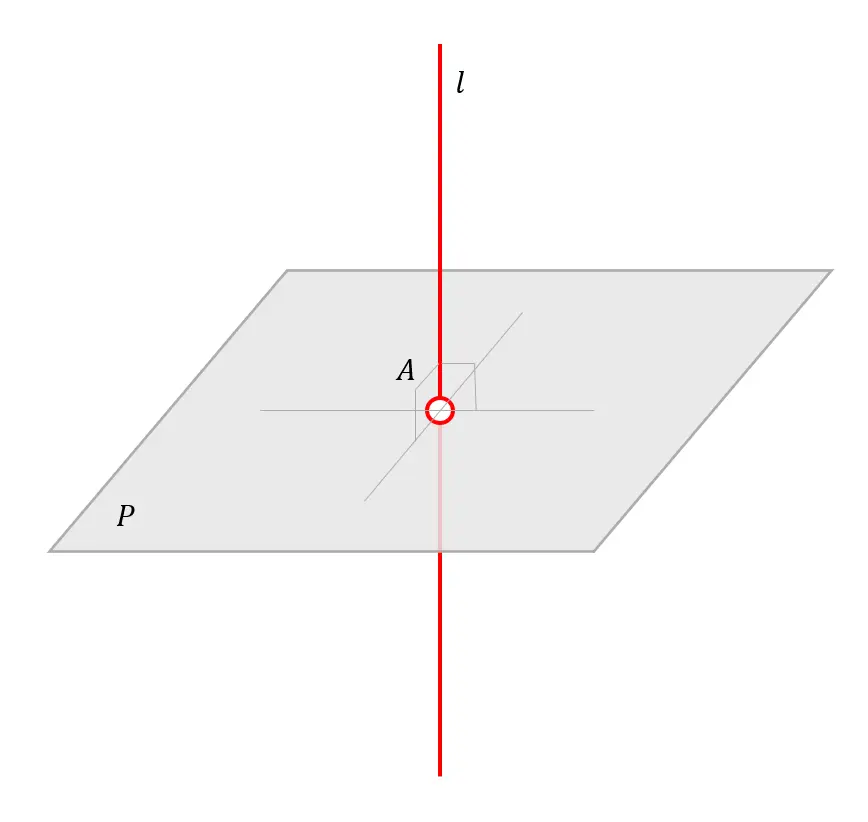
三维空间中二维空间 ( 平面 ) 和一维空间 ( L i n e ) 的正交情况 \large 三维空间中二维空间(平面)和一维空间(Line)的正交情况 三维空间中二维空间(平面)和一维空间(Line)的正交情况
如果是对于两个平面(二维欧式空间),它们在三维空间内是不可能正交的,它们只可能在四维空间中出现正交。
总结
矩阵
A
A
A的零空间
把
A
A
A看作是系统:
A
A
A的零空间,就是
A
x
=
0
Ax=0
Ax=0中,所有x组成的空间。
把
A
A
A看作是函数(变换):
A
A
A的零空间,所有被
A
A
A变化为
0
0
0点的所有向量组成的空间。
把
A
A
A看作是空间:
A
A
A的零空间,是和
A
A
A的行空间正交的向量空间。


























 1804
1804

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










