Simple Function
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
Knowing that x can be any real number that x 2 + Dx + E ≠ 0. Now, given the following function:
What is the range of y?
Input
The first line contains a single integer T (T ≤ 10000), indicating that there are T cases below.
Each case contains five integers in a single line which are values of A, B, C, D and E (-100 ≤ A, B, C, D, E ≤ 100).
Output
For each case, output the range of y in the form of standard interval expression like in a single line.
The expression is made up by one interval or union of several disjoint intervals.
Each interval is one of the following four forms: “(a, b)”, “(a, b]”, “[a, b)”, “[a, b]”(there is a single space between ‘,’ and ‘b’), where a, b are real numbers rounded to 4 decimal places, or “-INF” or “INF” if the value is negative infinity or positive infinity.
If the expression is made up by several disjoint intervals, put the letter ‘U’ between adjacent intervals. There should be a single space between ‘U’ and nearby intervals.
In order to make the expression unique, the expression should contain as minimum of intervals as possible and intervals should be listed in increasing order.
See sample output for more detail.
Sample Input
5
1 1 1 2 3
0 1 0 1 -10
-3 -1 0 -1 -1
0 0 0 0 0
1 3 0 2 0
Sample Output
[0.3170, 1.1830]
(-INF, INF)
(-INF, -1.8944] U [-0.1056, INF)
[0.0000, 0.0000]
(-INF, 1.0000) U (1.0000, 1.5000) U (1.5000, INF)
题目大意:给一个式子,让你求这个式子的值域。
思路:按照高中的求解思路不停的分类讨论,首先先把分子的二次项消除掉,然后分子就变成了一次项的,然后对分子中一次向系数和常数进行正负零讨论即可,代码不难,关键在于细心。
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <cstring>
#include <algorithm>
#include <string>
#include <set>
#include <functional>
#include <numeric>
#include <sstream>
#include <stack>
#include <map>
#include <queue>
#include<iomanip>
using namespace std;
#define ll long long
int main()
{
int t;
cin>>t;
while(t--)
{
double a,b,c,d,e,aa,bb,cc,bbb,ccc,t,midd;
scanf("%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e);
aa=a;
bb=b-a*d;
cc=c-a*e;
if(bb==0)
{
if(cc==0)
printf("[%.4f, %.4f]\n",a,a);
else if(cc<0)
{
midd=e-d*d/4;
if(midd>0)
printf("[%.4f, %.4f)\n",cc/midd+a,a);
printf("(-INF, %.4f) U [%.4f, INF)\n",a,cc/midd+a);
else
printf("(-INF, %.4f)\n",a);
}
else
{
midd=e-d*d/4;
printf("(%.4f, %.4f]\n",a,cc/midd+a);
else if(midd<0)
printf("(-INF, %.4f] U (%.4f, INF)\n",cc/midd+a,a);
printf("(%.4f, INF)\n",a);
}
}
else
{
double x1,x2,y,t1,t2;
x1=-cc/bb;
if(x1*x1+d*x1+e==0)
{
x2=-d-x1;
if(x1==x2)
printf("(-INF, %.4f) U (%.4f, INF)\n",a,a);
else
{
y=bb/(x1-x2);
printf("(-INF, %.4f) U (%.4f, %.4f) U (%.4f, INF)\n",a,a,a+y,a+y);
else
printf("(-INF, %.4f) U (%.4f, %.4f) U (%.4f, INF)\n",a+y,a+y,a,a);
}
}
else
{
bbb=d*bb-2.0*cc;
ccc=cc*cc+e*bb*bb-d*bb*cc;
printf("(-INF, INF)\n");
else
{
t1=2.0*sqrt(ccc);
t2=t1+bbb;
t1=bbb-t1;
if(t1>0)
printf("(-INF, %.4f] U [%.4f, INF)\n",a+bb*bb/t2,a+bb*bb/t1);
printf("(-INF, %.4f]\n",a+bb*bb/t2);
else if(t2<0)
printf("(-INF, %.4f] U [%.4f, INF)\n",a+bb*bb/t2,a+bb*bb/t1);
printf("[%.4f, INF)\n",a+bb*bb/t1);
else
printf("[%.4f, %.4f]\n",a+bb*bb/t1,a+bb*bb/t2);
}
}
}
}
return 0;
}







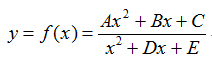
















 480
480

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








