
Betweenness Centrality (from wikipedia)
在图论中,介数中心性(英語:Betweenness Centrality)是基于最短路径针对网络图中心性的衡量标准之一。针对全连接网络图,其中任意两个节点均至少存在一个最短路径,在无权重网络图中该最短路径是路径包含边的数量求和,加权网络图中该最短路径则是路径包含边的权重求和。每个节点的介数中心性即为这些最短路径穿过该节点的次数。
Girvan-Newman algorithm (格里-纽曼算法)
1. 首先计算网络中所有现有边的介数。 2. 具有最高介数的边被去除。 3. 重新计算所有受移除影响的边的介数。 4. 重复步骤 2 和 3,直到所有的边都计算完。
Girvan-Newman example
1. 遍历所有边的介数,4-6,4-7这两条边的介数为10,移除4-6,重复计算所有受移除影响的边的介数
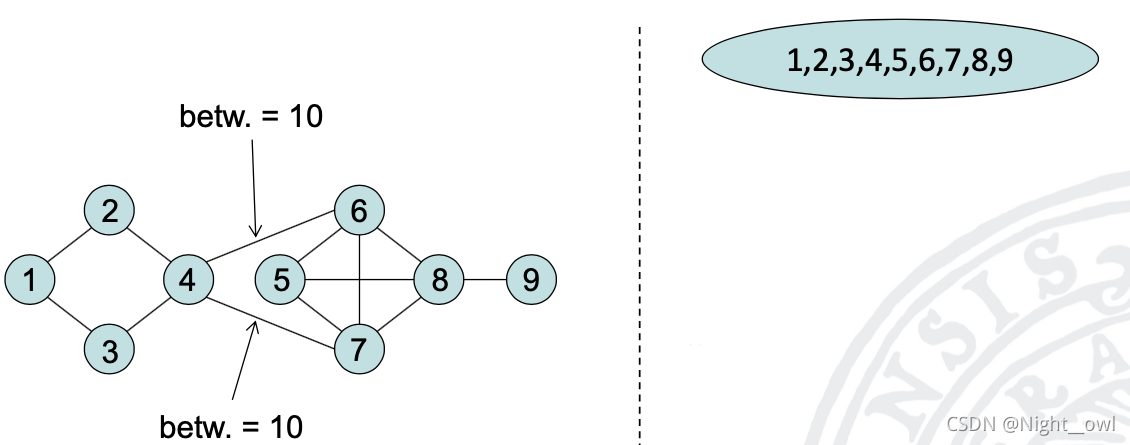
2.这里4-7的介数最大,那么就将这条边移除4-7。
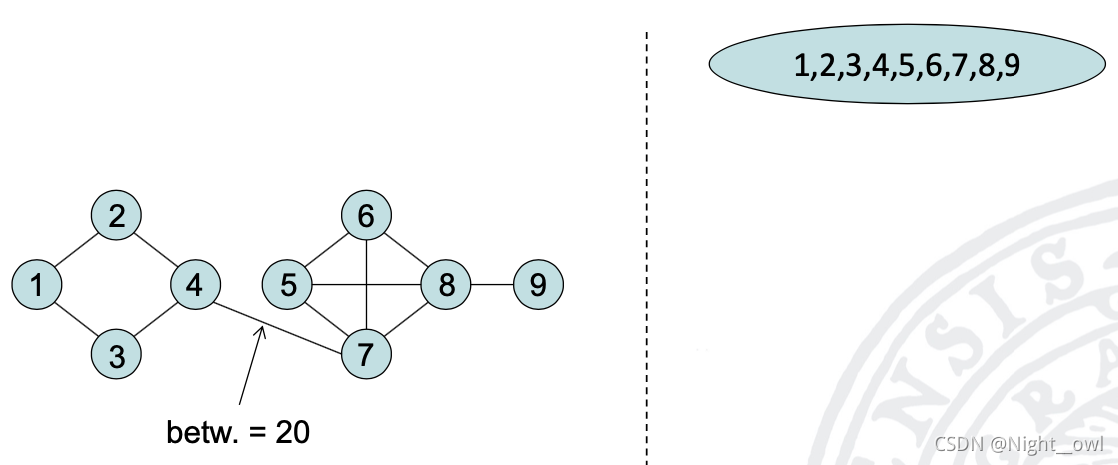 3. 移除之后我们可以看到,原来的一个图类变成了两个簇。然后重新计算图中的介数。
3. 移除之后我们可以看到,原来的一个图类变成了两个簇。然后重新计算图中的介数。
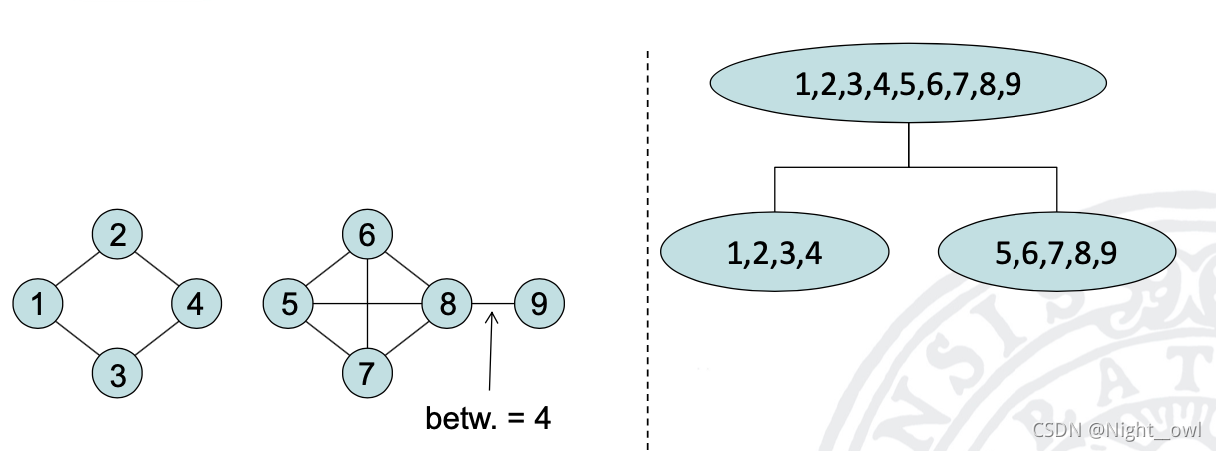
4. 最后一直迭代,可以得到以下簇分布。

Modularity(模块化)
模块化是衡量网络或图结构的度量,它衡量将网络划分为模块(也称为组、集群或社区)的强度。模块化程度高的网络,模块内节点间连接密集,不同模块间节点间连接稀疏。模块化通常用于检测网络中社区结构的优化方法。然而,已经表明模块化受到分辨率限制,因此无法检测小社区。包括动物大脑在内的生物网络表现出高度的模块化。下面是模块化计算的公式。
| 参数 | 定义 |
| m | 图中边的数量 |
| i,j | 节点标识 |
| 如果节点 i 和节点 j 是相连的,那么 | |
| 表示节点 i 的度(degree) | |
| 如果 a = b, value = 1, otherwise 0. | |
| community (社区|簇)标识 |
Modularity计算示例

Louvain Algorithm
该算法的核心思想很简单:
-
将图中所有的节点都看作一个个独立的社区,最开始社区的数目与节点的个数相同
-
对于节点 i ,依次分配到其他社区,并计算分配前和分配后的模块度(modularity)
,并记录最大的邻居节点,如果该值大于0,那么就将节点i分配到邻居节点所在的社区,否则保持不变。
-
重复2,直到所有节点的所属社区不再变化
-
得到的新的社区,可以进行图压缩,通俗地讲就是将同一社区节点压缩成一个新的节点,同时记录社区内节点之间的边的权重当作新节点的边的权重,社区间的边权重转化为新节点的度。
-
重复步骤1,直到整个图的模块度不再发生变化。
下面给出一个示例:
1. 每个节点扫一遍,对相邻的节点计算模块度,如果变化的模块度大于原先的模块度,则加入到新社区。





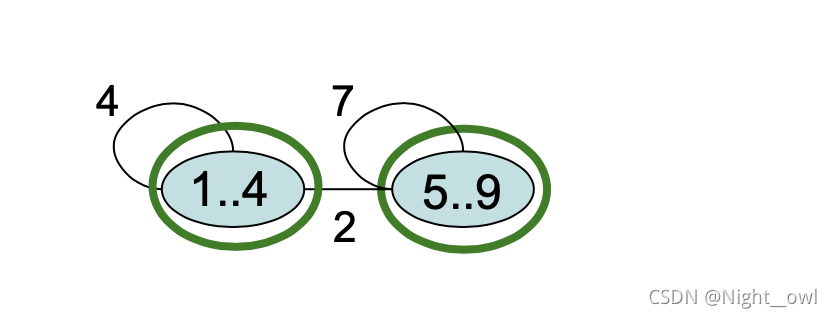
2. 压缩图,合并所有的社区,并计算内部的度,和其他社区连接的边数。

3. 扫第二轮,重复以上步骤



4. 扫第三轮,不做变化,得到最后的社区簇。

























 377
377

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








