One PUNCH Man——隐马尔可夫模型（HMM）

概率图模型简介

概率模型(probabilistic model)提供了一种描述框架，将学习任务归结于计算变量的概率分布。在概率模型中，利用已知变量推测未知变量的分布称为"推断" (inference) ，其核心是如何基于可观测变量推测出未知变量的条件分布。

• 生成式模型:从统计的角度表示数据的分布情况，能够反映同类数据本身的相似度，不关心判别边界。
  举例：
  判别式分析，朴素贝叶斯，K近邻(KNN)，混合高斯模型，隐马尔科夫模型(HMM)，贝叶斯网络，Sigmoid Belief Networks，马尔科夫随机场(Markov Random Fields)，深度信念网络(DBN)。
• 判别式模型：寻找不同类别之间的最优分类面，反映的是异类数据之间的差异。
  举例：
  线性回归(Linear Regression)，逻辑斯蒂回归(Logistic Regression)，神经网络(NN)，支持向量机(SVM)，高斯过程(Gaussian Process)，条件随机场(CRF)，CART(Classification and Regression Tree)

概率图模型(probabilistic graphical model)是一类用图来表达变量相关关系的概率模型。它以图为表示工具，最常见的是用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系。

概率图模型可大致分为两类:第一类是使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网(Bayesian network)；第二类是使用无向图表示变量间的相关关系，称为无向图模型或马尔可夫网(Markov network)。

HMM

HMM是一种著名的有向图模型，主要用于时序数据建模，在语音识别、自然语言处理等领域有广泛应用。
隐马尔可夫模型的图结构如下：

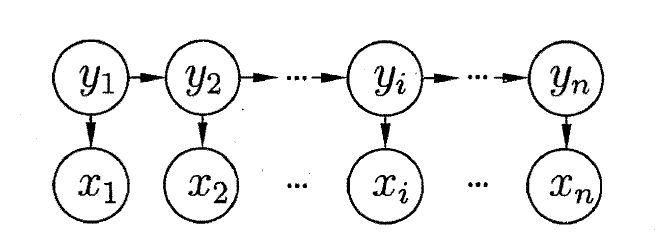
隐马尔可夫模型包含三个要点：

• 隐变量：包含隐含状态数量和隐含状态链，上图表现为 { y 1 , y 2 , . . . , y n } \{y_1,y_2,...,y_n\} {y1​,y2​,...,yn​}的n个隐含状态的有向链，从$y_i$到$y_{i+1}$的概率表示为$P(y_{i+1}|y_i)$。
• 观测变量：包括可见状态及其概率，上图表现为可见的观测值$(x_1,x_2,...,x_n)$，以及在隐含状态$y_i$下取得观测值$x_i$的概率$P(x_i|y_i)$。
• 初始状态概率：初始隐含状态是$y_i$的概率$P(y_i)$

举个例子：
有下图三种骰子：

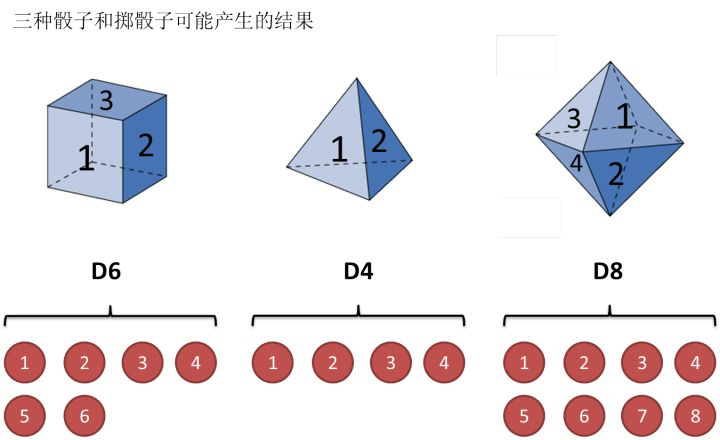
假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）： { 1 , 6 , 3 , 5 , 2 , 7 , 3 , 5 , 2 , 4 } \{1, 6, 3, 5, 2, 7, 3, 5, 2, 4\} {1,6,3,5,2,7,3,5,2,4}

这一串数字，就是我们之前说的，$(x_1,x_2,...,x_n)$，也就是这一系列数字，是我们肉眼直接观测到的，即观测变量。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是： { D 6 , D 8 , D 8 , D 6 , D 4 , D 8 , D 6 , D 6 , D 4 , D 8 } \{D6, D8, D8, D6, D4, D8, D6, D6, D4, D8\} {D6,D8,D8,D6,D4,D8,D6,D6,D4,D8}，对应到我们之前说的 { y 1 , y 2 , . . . , y n } \{y_1,y_2,...,y_n\} {y1​,y2​,...,yn​}。这个部分，我们在结果中是不可直接看到的，所以是隐含的。

一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）$P(x_i|y_i)$。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。

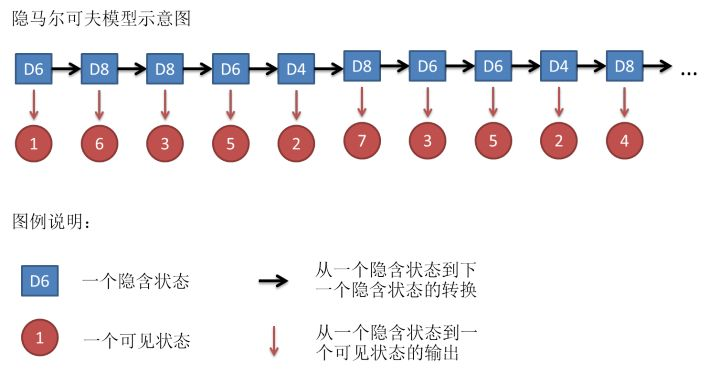
其实对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但是应用HMM模型时候呢，往往是缺失了一部分信息的，有时候你知道骰子有几种，每种骰子是什么，但是不知道掷出来的骰子序列；有时候你只是看到了很多次掷骰子的结果，剩下的什么都不知道。如果应用算法去估计这些缺失的信息，就成了一个很重要的问题。这些算法我会在下面详细讲。

现在，我们定义三个集合和两个矩阵，来完善之前的概率P：

1. 系统隐含状态集合，称为状态空间：$\gamma =(s_1,s_2,...,s_N)$，取值个数为N；系统观测状态集合，称为观测空间：$\chi =(o_1,o_2,...,o_M)$，取值个数为M。
2. 状态转移概率矩阵$A$：
   记为$A=[a_{ij}{]}_{N\times N}$
   其中，$a_{ij}=P(y_{t+1}=s_j|y_t=s_i)$，即当前状态是$s_i$的情况下，下一状态是$s_j$的概率
3. 输出观测概率矩阵$B$：
   记为矩阵$B=[b_{ij}{]}_{N\times M}$
   其中，$b_{ij}=P(x_t=o_j|y_t=s_i)$，即当前隐含状态是$s_i$的情况下，观测值是$o_j$的概率。
4. 初始概率集合：模型在初始时刻各状态出现的概率，通常记为$\pi =({\pi }_1,{\pi }_2,...,{\pi }_N)$，取值个数为N
   其中，${\pi }_i=P(y_t=s_i)$，即初始隐含状态是$s_i$的概率。

我们指定状态空间$\gamma$，观测空间$\chi$，以及状态转移概率矩阵$A$， 输出观测概率矩阵$B$， 初始概率集合$\pi$，就能确定一个马尔可夫隐型。 通常，用 $\lambda =[A,B,\pi ]$ 表示。

好了，现在来讨论实际应用中所遇到的问题。前面说了，实际问题往往是缺失一部分信息的，我们来看看，一个马尔可夫隐型有哪些信息：

1. $\lambda =[A,B,\pi ]$
2. { y 1 , y 2 , . . . , y n } \{y_1,y_2,...,y_n\} {y1​,y2​,...,yn​}
3. $(x_1,x_2,...,x_n)$

上述三点很简单，就是说的概率模型和产生的隐马尔可夫状态链和观测序列。现在，引出我们一直要讨论的 三类问题 ：

1. 给定模型$\lambda =[A,B,\pi ]$，计算产生观测序列$x=(x_1,x_2,...,x_n)$的概率$P(x|\lambda )$？换言之，如何评估模型$\lambda$与观测序列的匹配程度。
   形象地用之前的栗子描述：知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。
2. 给定模型$\lambda =[A,B,\pi ]$和观测序列$x=(x_1,x_2,...,x_n)$，如何找到与此观测序列最匹配的状态链 y = { y 1 , y 2 , . . . , y n } y=\{y_1,y_2,...,y_n\} y={y1​,y2​,...,yn​}？换言之，如何根据观测序列推断出隐藏的模型状态。
   也是用之前的栗子描述：知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。
3. 给定观测序列$x=(x_1,x_2,...,x_n)$，如何调整模型$\lambda =[A,B,\pi ]$的参数，使得该序列出现的概率$P(x|\lambda )$最大？换言之，如何训练模型使其能够最好的描述观测数据。
   同样用之前的栗子描述：知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）。

上述问题在现实应用中非常重要。例如，许多任务需根据以往的观测序列$x=(x_1,x_2,...,x_{n-1})$，来推测现在最有可能的观测值$x_n$，即第一种问题。
在语音识别等任务中，观测值为语音信号，隐藏状态为文字，目标就是根据观测信号来推断最有可能的状态序列(即对应的文字)，即上述第二个问题。在大多数现实应用中，人工指定模型参数已变得越来越不可行，如何根据训练样本学得最优的模型参数，恰是上述第三个问题。

感觉后面的内容，都是用于解决NLP的一系列问题，书中介绍的时候，有些概念没介绍清楚（或者说我基础不够，可能了解统计学的人能够更明白那些概念），所以暂且学到这里，对于马尔可夫随机场，只能表示以后有机会再学吧。

参考文献：
https://www.zhihu.com/question/20962240 知乎 Yang Eninala
《机器学习》周志华