系列文章目录
文章目录
前言
马克思说过:“一门学科只有成功地运用数学时,才算达到了完善的地步。”
美国国家科学院的一位院士总结了将数学科学转化为生产力的成功于失败,得出了“数学一种关键的、普遍的、可以应用的技术”的结论,认为数学“由研究到工业领域的技术转化,对加强经济竞争力具有重要意义”,而“计算机和建模重新成为课题中心,他们是数学科学技术转化的重要途径”。
作为一名计算机专业的学生,已经逐渐在各个学科中看见数学建模的重要性,本系列作为我个人第一个系统性自学学科的笔记,有任何问题欢迎指正。
1.1 从现实对象到数学模型
原型(Prototype)和模型(Model)是一对对偶体。
- 原型:是指人们在现实生活中关心、研究或者从事生产、管理的实际对象,在科技领域通常使用系统、过程等词汇。
- 模型:为了某个特定的目的将原型的一部分信息简缩、提炼而构造的原型替代物。
- 模型的形式:物质模型(形象模型)、理想模型(抽象模型);
物质模型 包括:直观模型(实物模型、照片)、物理模型,
理想模型 包括:思维模型(经验、技术)、符号模型(使用符号线条,地图、电路图)、
数学模型。
- 数学模型:
对于现实世界的一个特定对象,为了一个特定目的,根据特有的内在规律,作出
一些必要的简化假设,运用一些适当的数学工具,得到一个数学结构。
- 计算机模拟:与数学模型有密切相关的数学模拟,主要指运用数字式计算机的计算机模拟。
- 具体的应用:分析与设计 、预报与决策、控制与优化、规划与管理
1.2 数学建模的基本方法与步骤
- 基本方法:机理分析和测试分析
- 机理分析:根据对客观事物特性的认识,找出反映内部机理的数量规律,建立的模型常有 明确的物理或现实意义。后面三个示例都是机理分析。机理分析主要通过实例研究。
- 测试分析:是将研究系统看作一个“黑箱”系统(内部机理看不清楚),通过对系统的输入与输出数据的测量和统计分析,按照一定的准则找出与数据拟合的很好的模型。测试分析有一套完整的数学体系。
- 实际问题中常常使用两种方法结合来建模:即机理分析建立模型的结构,用测试分析确定模型的参数
- 步骤
- 模型准备:了解问题的实际背景,明确建模目的,搜集必要的信息入现象、数据等,尽量弄清对象的主要特征,形成一个比较清晰的“问题”,由此初步确定用哪一类模型。情况才能方法对。在模型准备阶段要深入调查,虚心向实际工作者请教,尽量掌握第一手资料。
- 模型假设:根据对象的特征和建模目的,抓住问题的本事,忽略次要因素,作出必要的、合理的简化假设。
- 模型构成:根据所做的假设,用数学的语言、符号描述对象的内在规律,建立包含包含常量、变量等的数学模型,如优化模型、微分方程模型、差分方程模型、图的模型等。
- 模型求解:可以采用解方程、画图形、优化方法、数值计算、统计分析等各种数学方法,特别是数学软件和计算机技术。
- 模型分析:对求解结果进行数学上的分析,如结果的误差分析、统计分析、模型对数据的
- 模型检验:把求解和分析的结果翻译会到实际问题,与实际的现象、数据比较,检验模型的合理性和适用性。如果与实际不符,问题常出现在模型假设上,应修改、补充假设,重新建模,有些模型需要经过几次反复,不断建模,直到检验结果获得某种程度上的满意。
- 模型应用:应用的方式与问题性质、建模目的及最终的结果有关。
需要指出,不是所有的建模都要经过以上步骤,不要拘泥于形式,灵活建模

1.3 数学模型的特点与分类
- 数学模型的特点
逼真性和可行性、渐进性、可转移性、非预制性、条理性、技艺性、局限性
- 模型的分类
1.按照应用领域分(人口、交通、生态、生物数学、数学经济学模型等等)
2.按所建立模型的数学方法分(初等模型、几何模型、微分方程、统计回归、数学规划模型)
3.按照模型的表现性分
1) 确定性模型和随机模型
2) 静态模型和动态模型
3) 线性模型和非线性模型
4) 离散模型和连续模型
4.按照建模的目的分 (描述、预报、优化、决策、控制模型)
5.按照对模型结构的了解程度分(白象、灰箱、黑箱)
1.4 从三个建模示例来了解数学建模
以下我们将从三个简单模型来初步了解建模的过程,采用的方法都是机理分析。
-
示例一 椅子能在不平的地面上放平稳吗?
问题描述
情境:一个日常生活中的普通事实,把椅子往不平的地面上一放,通常只有三只脚着地,放不稳,然而只需要挪动几次,就可以使四只脚同时着地,放稳了。这个看似与数学无关的现象能用数学语言表述,并用数学工具证实吗?
模型假设
对椅子和地面应该作一些必要的假设
1. 假设椅子的四条腿一样长,椅子腿与地面接触处抽象为一个点,四脚的连线呈正方形
2. 地面高度是连续变化的,沿任何方向都不会出现间断(不是台阶),可以看做一个连续曲面。(地面不会出现深沟或者凸峰)
3.相对于椅子脚的间距和本身椅子腿的长度而言,地面是相对椅子平坦的,(如果把椅子脚看成质点,那么地面的起伏可以忽略不计)在任何时候椅子至少要能有三条腿着地。
模型构成
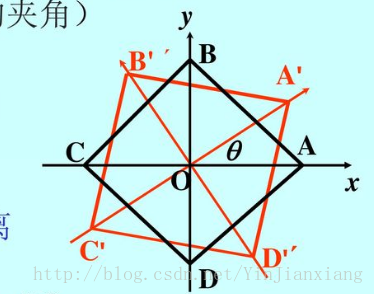
- 首先,要用变量表示椅子的位置,发现我们可以用旋转的角度(椅子腿对角线 AC 与 x 轴的夹角) θ 来表示椅子的位置
- 其次,我们需要用数学语言来描述椅子脚着地(椅子腿距地面的距离竖直,当它为0时,即为着地)所以这个函数是关于θ的函数,
- 对于四个椅子腿,由于正方形的中心对称性,我们只需要设两个距离函数:
A,C 两脚距离地面的距离和 f(θ)
B,D 两脚距离地面的距离和 g(θ)
我们看到这两个函数都是关于椅子位置(θ)的函数,并且根据我们之前的假设3,我们可以知道这两个函数都是连续函数。由假设三,椅子在任意位置都是三只脚着地,所以对于任意的θ,f(θ)和g(θ)至少有一个不为0,不妨设g(θ)=0,f(θ)>0,而当椅子旋转90°后,对角线AC和BD互换,于是有f(π/2)=0,g(π/2)>0。
这样,改变椅子的位置使四只脚同时着地,就归结为如下的数学命题
已知 f(x) 和 g(x) 是关于 θ 的连续函数,对于任意的 θ ,f(x) * g(x) = 0 ,且 g(0) = f(π/2) = 0, f(0) > 0 , g(π/2) > 0 。证明:存在一个角度θ0,使得f(θ0) = g(θ0) = 0
模型求解
令h(θ)=f(θ)-g(θ),得h(0)>0,h(π/2)<0.
且h(0)<0由f和g的连续性可知h为连续函数。
根据连续函数的基本性质(零点存在性定理)
必然存在 θ0(0<θ0<π/2),使得h(θ0)=0,即f(θ0)=g(θ0)
最后,因为f(θ0) * g(θ0)=0,所以f(θ0)=g(θ0)=0。
结论:椅子一定能放稳。
由于模型比较简单,模型解释和验证就省略了
评注
- 模型的巧妙之处在于用一元变量θ去表示椅子的位置,用关于θ的两个函数来表示椅子四脚与地面的距离
- 模型中的假设一中的“四脚的连线呈正方形”,不是本质的,可以考虑四角连线呈长方形的情况
- 建模过程中的不严谨之处:椅子的旋转轴在哪里,它在旋转过程中怎么变化?
更严谨的一种考虑如下:
取A,B,D脚同时着地的位置为初始状态,经过O点且与A,B,D脚所在平面垂直的直线为初始的旋转轴。此后将椅子沿该轴搞搞举起,并在与该轴垂直的平面逆时针旋转后再慢慢放下。放下的过程中,保持新的旋转轴始终通过O点但允许发生倾斜,使得A,B脚先着地,再让D,C两脚中至少一个着地(尽可能先让D脚着地)。
-
示例二 商人们怎样安全渡河
-
示例三 如何施救药物中毒
二、三两个示例以及示例一的长方形假设将在以后的更新给出解答
1.4.5 数学建模系统的思维导图
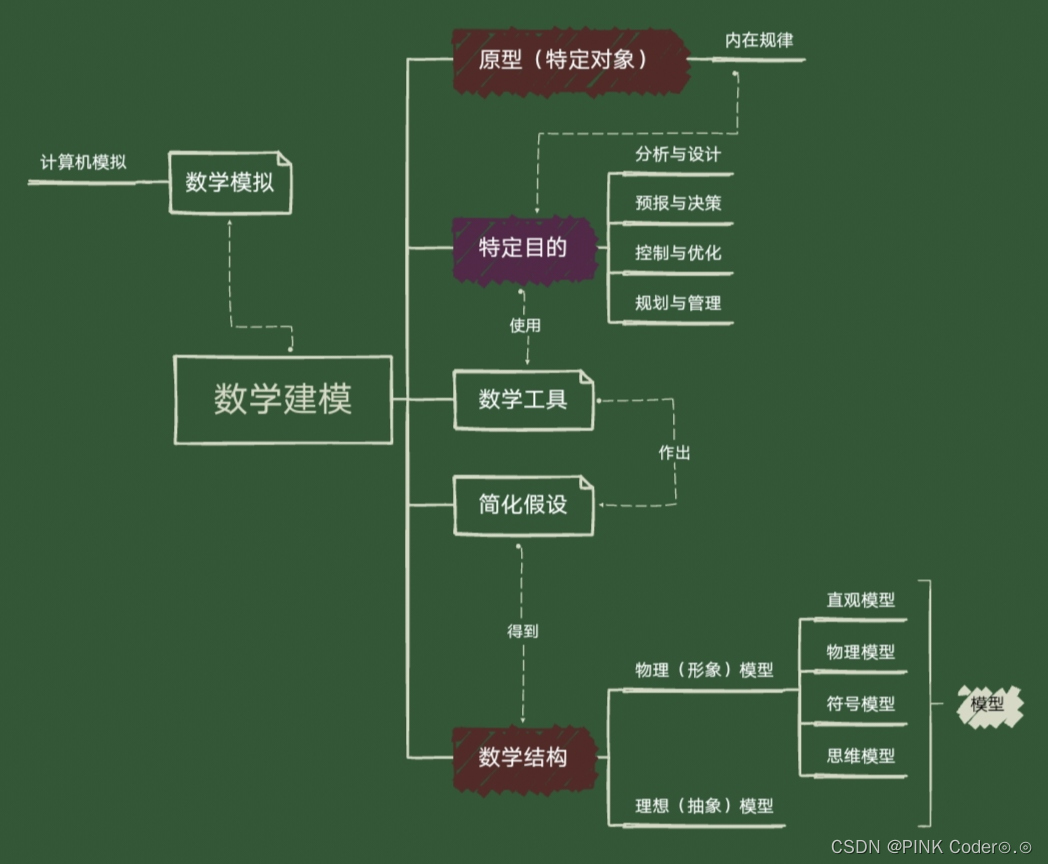
-
新人博主,有收获的同学的点个关注,如有错误的地方请指正
- 参考文献
-
[1] 《数学建模》(第四版) 高等教育出版社






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








