深度强化学习DDPG实现路径跟踪（局部规划器）方法讲解与PyTorch代码实现

代码仓库地址：https://github.com/ai-winter/python_motion_planning

参考文献：深度强化学习（王树森等 著）

博客文章只写核心代码，不包含环境和各类utils代码，如果要运行请pull完整仓库代码（仓库代码里还有很多路径规划、路径跟踪和曲线生成算法，如果对您有帮助，请给我们仓库一个小小的star，谢谢啦~）。

算法选择

传统的路径跟踪（局部规划器）使用的是DWA等基于采样的算法，或者PID、LQR、MPC等基于控制的算法，这类控制算法解决的问题一般可以用强化学习解决。

强化学习算法又分为多种， Q学习 是最经典的强化学习算法之一，维护一个Q-Table，输入离散的状态空间，输出离散的动作空间。 深度Q学习 用一个 深度Q网络（Deep Q Network，DQN） 代替了Q-Table，用DQN来近似动作价值函数 $Q(s,a)$ ，可以输入连续的状态空间，输出的是每个动作的价值，最后决策的时候取最高价值的动作。然而，我们做路径跟踪，一般来说状态空间和动作空间都是连续的。如果使用深度Q学习，我们需要将动作空间分割成离散的，然后DQN需要输出每个离散动作的价值，计算代价相当之高，神经网络拟合较困难，而且动作的精度低。

有什么DRL算法可以解决连续动作空间问题呢？对于我们这样一个连续状态空间和连续动作空间的问题，最经典的算法就是 深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG） ，发表它的论文是Continuous control with deep reinforcement learning。

算法介绍与实现

神经网络

DDPG是一种Actor-Critic方法，它有一个策略网络（演员），一个价值网络（评委）。

• 策略网络（Actor） 控制智能体做运动，它基于状态 $s$ 做出动作 $a$ ，记为 $\mu (s)$ ，输入连续的状态空间，输出每一个动作的确定值。
• 价值网络（Critic） 不控制智能体，只是基于状态 $s$ 给动作 $a$ 打分，记为 $q(s,a)$ ，输入连续的状态+动作，输出评分，从而指导策略网络做出改进。
  

在PyTorch代码实现中，我们可以用简单的 多层感知机（Multi-Layer Perceptron，MLP） 来作为策略网络和价值网络。但多层感知机拟合能力较差，训练很容易达到瓶颈，如果计算资源充足，可以尝试将地图障碍物先验信息传入CNN等更复杂的神经网络一并训练。

class Actor(nn.Module):
    """
    Actor network to generate the action.

    Parameters:
        state_dim (int): state dimension
        action_dim (int): action dimension
        hidden_depth (int): the number of hidden layers of the neural network
        hidden_width (int): the number of neurons in hidden layers of the neural network
        min_state (torch.Tensor): minimum of each value in the state
        max_state (torch.Tensor): maximum of each value in the state
        min_action (torch.Tensor): minimum of each value in the action
        max_action (torch.Tensor): maximum of each value in the action
    """
    def __init__(self, state_dim: int, action_dim: int, hidden_depth: int, hidden_width: int,
                 min_state: torch.Tensor, max_state: torch.Tensor, min_action: torch.Tensor, max_action: torch.Tensor) -> None:
        super(Actor, self).__init__()
        self.min_state = min_state
        self.max_state = max_state
        self.min_action = min_action
        self.max_action = max_action

        self.hidden_depth = hidden_depth
        self.input_layer = nn.Linear(state_dim, hidden_width)
        self.hidden_layers = nn.ModuleList([nn.Linear(hidden_width, hidden_width) for _ in range(self.hidden_depth)])
        self.output_layer = nn.Linear(hidden_width, action_dim)

    def forward(self, s: torch.Tensor) -> torch.Tensor:
        """
        Generate the action based on the state.

        Parameters:
            s (torch.Tensor): state

        Returns:
            a (torch.Tensor): action
        """
        # normalization
        s = (s - self.min_state) / (self.max_state - self.min_state)

        s = F.relu(self.input_layer(s))
        for i in range(self.hidden_depth):
            s = F.relu(self.hidden_layers[i](s))
        s = self.output_layer(s)
        a = self.min_action + (self.max_action - self.min_action) * torch.sigmoid(s)  # [min,max]
        return a


class Critic(nn.Module):
    """
    Critic network to estimate the value function q(s,a).

    Parameters:
        state_dim (int): state dimension
        action_dim (int): action dimension
        hidden_depth (int): the number of hidden layers of the neural network
        hidden_width (int): the number of neurons in hidden layers of the neural network
        min_state (torch.Tensor): minimum of each value in the state
        max_state (torch.Tensor): maximum of each value in the state
        min_action (torch.Tensor): minimum of each value in the action
        max_action (torch.Tensor): maximum of each value in the action
    """
    def __init__(self, state_dim: int, action_dim: int, hidden_depth: int, hidden_width: int,
                 min_state: torch.Tensor, max_state: torch.Tensor, min_action: torch.Tensor, max_action: torch.Tensor) -> None:
        super(Critic, self).__init__()
        self.min_state = min_state
        self.max_state = max_state
        self.min_action = min_action
        self.max_action = max_action

        self.hidden_depth = hidden_depth
        self.input_layer = nn.Linear(state_dim + action_dim, hidden_width)
        self.hidden_layers = nn.ModuleList([nn.Linear(hidden_width, hidden_width) for _ in range(self.hidden_depth)])
        self.output_layer = nn.Linear(hidden_width, 1)

    def forward(self, s: torch.Tensor, a: torch.Tensor) -> torch.Tensor:
        """
        Calculate the Q-value of (s,a)

        Parameters:
            s (torch.Tensor): state
            a (torch.Tensor): action

        Returns:
            q (torch.Tensor): Q-value of (s,a)
        """
        # normalization
        s = (s - self.min_state) / (self.max_state - self.min_state)
        a = (a - self.min_action) / (self.max_action - self.min_action)

        input = torch.cat([s, a], axis=-1)

        q = F.relu(self.input_layer(input))
        for i in range(self.hidden_depth):
            q = F.relu(self.hidden_layers[i](q))
        q = self.output_layer(q)
        return q

经验回放

DDPG是个 异策略（Off-Policy） 算法，行为策略（Behavior Policy） 可以不同于 目标策略（Target Policy） 。
行为策略在训练开始时可以随机探索，将探索到的 $(s,a,r,s^{\prime })$ 四元组数据加入 经验回放缓存（Experience Replay Buffer） ，当探索到了足够的数据后，就可以开始训练目标策略，行为策略改为在目标策略上加一个随机噪声，从而在不断进化地前提上保持探索。

在代码实现中，我写了一个最基础的经验回放缓存。

四元组改为了五元组，加了一个"win"布尔变量，意思是如果成功到达终点（win），就终结马尔可夫决策过程（Markov Decision Process，MDP），不加上预期未来回报，否则要加上。 回报（Return） 是指 奖励（Reward） 在MDP中的累积值，通常使用 折扣回报（Discounted Return） 计算，公式是 $u_t={\sum }_{i=t}^n{\gamma }^{i-t}\cdot r_i$。在成功到达终点时终结MDP的好处是鼓励智能体更快到达终点，因为后面设计的奖励函数每一步都会有一个负的与终点距离的惩罚值，回报会对这些惩罚值累积，时间越久累积越多，所以越早到达终点，累积的惩罚越小。撞到障碍物（lose）就不终结MDP，否则会鼓励智能体尽早撞障碍物。

这个经验回放缓存还可以进行优化，可以改为 优先经验回放缓存（Prioritized Experience Replay Buffer） ，用SumTree来以 $O(logn)$ 的时间复杂度抽样。

class ReplayBuffer(object):
    """
    Experience replay buffer to store the transitions.

    Parameters:
        state_dim (int): state dimension
        action_dim (int): action dimension
        max_size (int): maximum replay buffer size
        device (torch.device): device to store the data
    """
    def __init__(self, state_dim: int, action_dim: int, max_size: int, device: torch.device) -> None:
        self.max_size = max_size
        self.count = 0
        self.size = 0
        self.s = torch.zeros((self.max_size, state_dim), dtype=torch.float, device=device)
        self.a = torch.zeros((self.max_size, action_dim), dtype=torch.float, device=device)
        self.r = torch.zeros((self.max_size, 1), dtype=torch.float, device=device)
        self.s_ = torch.zeros((self.max_size, state_dim), dtype=torch.float, device=device)
        self.win = torch.zeros((self.max_size, 1), dtype=torch.bool, device=device)

    def store(self, s: torch.Tensor, a: torch.Tensor, r: torch.Tensor, s_: torch.Tensor, win: bool) -> None:
        """
        Store a new transition in the replay buffer.

        Parameters:
            s (torch.Tensor): state
            a (torch.Tensor): action
            r (torch.Tensor): reward
            s_ (torch.Tensor): next state
            win (bool): win or otherwise, True: win (reached the goal), False: otherwise.
        """
        self.s[self.count] = s
        self.a[self.count] = a
        self.r[self.count] = r
        self.s_[self.count] = s_
        self.win[self.count] = torch.tensor(win, dtype=torch.bool)
        self.count = (self.count + 1) % self.max_size  # When the 'count' reaches max_size, it will be reset to 0.
        self.size = min(self.size + 1, self.max_size)  # Record the number of  transitions

    def sample(self, batch_size: int) -> tuple:
        """
        Sample a batch of transitions from the replay buffer.

        Parameters:
            batch_size (int): batch size

        Returns:
            batch_s (torch.Tensor): batch of states
            batch_a (torch.Tensor): batch of actions
            batch_r (torch.Tensor): batch of rewards
            batch_s_ (torch.Tensor): batch of next states
            batch_win (torch.Tensor): batch of win or otherwise, True: win (reached the goal), False: otherwise.
        """
        index = torch.randint(self.size, size=(batch_size,))  # Randomly sampling
        batch_s = self.s[index]
        batch_a = self.a[index]
        batch_r = self.r[index]
        batch_s_ = self.s_[index]
        batch_win = self.win[index]

        return batch_s, batch_a, batch_r, batch_s_, batch_win

算法类与环境

在DDPG算法类中，我定义了若干个参数与函数，每个参数与函数的意思写在了注释中。

• 模型保存地址： 两个神经网络的save_path是训练过程中最佳模型的保存地址，load_path是测试模型的加载地址。
• 训练曲线可视化： 训练过程可以在tensorboard可视化。
• 路径跟踪测试： plan和run函数是用于调用我们代码仓库中的环境，并调用全局路径规划器（默认A*），再让DDPG进行路径跟踪的测试。
• 环境： reset函数、step函数都是根据我们代码仓库中之前编写的用于路径跟踪算法的环境来写的，reset函数用于重置环境，step函数用于在环境中执行一个状态和动作对应的下一步，如果您在其它环境中使用该DDPG，应该重写reset函数和step函数。
• 奖励函数： 每一步中，距离目标越近奖励越高（进行了归一化），如果到达了目标（win），立即加一个较大的奖励（max_episode_steps），如果撞到了障碍物（lose），也会有一个比较大的惩罚（0.2*max_episode_steps）。

class DDPG(LocalPlanner):
    """
    Class for Deep Deterministic Policy Gradient (DDPG) motion planning.

    Parameters:
        start (tuple): start point coordinate
        goal (tuple): goal point coordinate
        env (Env): environment
        heuristic_type (str): heuristic function type
        hidden_depth (int): the number of hidden layers of the neural network
        hidden_width (int): the number of neurons in hidden layers of the neural network
        batch_size (int): batch size to optimize the neural networks
        buffer_size (int): maximum replay buffer size
        gamma (float): discount factor
        tau (float): Softly update the target network
        lr (float): learning rate
        train_noise (float): Action noise coefficient during training for exploration
        random_episodes (int): Take the random actions in the beginning for the better exploration
        max_episode_steps (int): Maximum steps for each episode
        update_freq (int): Frequency (times) of updating the network for each step
        update_steps (int): Update the network for every 'update_steps' steps
        evaluate_freq (int): Frequency (times) of evaluations and calculate the average
        evaluate_episodes (int): Evaluate the network every 'evaluate_episodes' episodes
        actor_save_path (str): Save path of the trained actor network
        critic_save_path (str): Save path of the trained critic network
        actor_load_path (str): Load path of the trained actor network
        critic_load_path (str): Load path of the trained critic network
        **params: other parameters can be found in the parent class LocalPlanner

    Examples:
        >>> from python_motion_planning.utils import Grid
        >>> from python_motion_planning.local_planner import DDPG
        # Train the model, only for learning-based planners, such as DDPG
		# It costs a lot of time to train the model, please be patient.
		# If you want a faster training, try reducing num_episodes and batch_size,
		# or increasing update_steps and evaluate_episodes, or fine-tuning other hyperparameters
		# if you are familiar with them, usually in a cost of performance, however.
		>>> plt = DDPG(start=(5, 5, 0), goal=(45, 25, 0), env=Grid(51, 31),
			   actor_save_path="models/actor_best.pth", critic_save_path="models/critic_best.pth")
		>>> plt.train(num_episodes=10000)
		
		# load the trained model and run
		>>> plt = DDPG(start=(5, 5, 0), goal=(45, 25, 0), env=Grid(51, 31),
			   actor_load_path="models/actor_best.pth", critic_load_path="models/critic_best.pth")
		>>> plt.run()


    References:
        [1] Continuous control with deep reinforcement learning
    """
    def __init__(self, start: tuple, goal: tuple, env: Env, heuristic_type: str = "euclidean",
                 hidden_depth: int = 3, hidden_width: int = 512, batch_size: int = 2000, buffer_size: int = 1e6,
                 gamma: float = 0.999, tau: float = 1e-3, lr: float = 1e-4, train_noise: float = 0.1,
                 random_episodes: int = 50, max_episode_steps: int = 200,
                 update_freq: int = 1, update_steps: int = 1, evaluate_freq: int = 50, evaluate_episodes: int = 50,
                 actor_save_path: str = "models/actor_best.pth",
                 critic_save_path: str = "models/critic_best.pth",
                 actor_load_path: str = None,
                 critic_load_path: str = None,
                 **params) -> None:
        super().__init__(start, goal, env, heuristic_type, **params)
        # DDPG parameters
        self.hidden_depth = hidden_depth        # The number of hidden layers of the neural network
        self.hidden_width = hidden_width        # The number of neurons in hidden layers of the neural network
        self.batch_size = int(batch_size)       # batch size to optimize the neural networks
        self.buffer_size = int(buffer_size)     # maximum replay buffer size
        self.gamma = gamma                      # discount factor
        self.tau = tau                          # Softly update the target network
        self.lr = lr                            # learning rate
        self.train_noise = train_noise          # Action noise coefficient during training for exploration
        self.random_episodes = random_episodes  # Take the random actions in the beginning for the better exploration
        self.max_episode_steps = max_episode_steps  # Maximum steps for each episode
        self.update_freq = update_freq          # Frequency (times) of updating the network for each step
        self.update_steps = update_steps        # Update the network for every 'update_steps' steps
        self.evaluate_freq = evaluate_freq      # Frequency (times) of evaluations and calculate the average
        self.evaluate_episodes = evaluate_episodes      # Evaluate the network every 'evaluate_episodes' episodes
        self.actor_save_path = actor_save_path      # Save path of the trained actor network
        self.critic_save_path = critic_save_path    # Save path of the trained critic network
        self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
        print(f"Using device: {self.device}")

        self.n_observations = 8     # x, y, theta, v, w, g_x, g_y, g_theta
        self.n_actions = 2          # v_inc, w_inc

        self.min_state = torch.tensor([0, 0, -math.pi, self.params["MIN_V"], self.params["MIN_W"], 0, 0, -math.pi],
                                      device=self.device)
        self.max_state = torch.tensor([self.env.x_range, self.env.y_range, math.pi, self.params["MAX_V"],
                                       self.params["MAX_W"], self.env.x_range, self.env.y_range, math.pi,], device=self.device)
        self.min_action = torch.tensor([self.params["MIN_V_INC"], self.params["MIN_W_INC"]], device=self.device)
        self.max_action = torch.tensor([self.params["MAX_V_INC"], self.params["MAX_W_INC"]], device=self.device)

        self.actor = Actor(self.n_observations, self.n_actions, self.hidden_depth, self.hidden_width, self.min_state,
                           self.max_state, self.min_action, self.max_action).to(self.device)
        if actor_load_path:
            self.actor.load_state_dict(torch.load(actor_load_path))
        self.actor_target = copy.deepcopy(self.actor)

        self.critic = Critic(self.n_observations, self.n_actions, self.hidden_depth, self.hidden_width,
                             self.min_state, self.max_state, self.min_action, self.max_action).to(self.device)
        if critic_load_path:
            self.critic.load_state_dict(torch.load(critic_load_path))
        self.critic_target = copy.deepcopy(self.critic)

        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=self.lr, weight_decay=1e-4)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=self.lr, weight_decay=1e-4)

        self.actor_scheduler = ReduceLROnPlateau(self.actor_optimizer, mode='max', factor=0.2, patience=10)
        self.critic_scheduler = ReduceLROnPlateau(self.critic_optimizer, mode='max', factor=0.2, patience=10)

        self.criterion = nn.MSELoss()

        self.replay_buffer = ReplayBuffer(self.n_observations, self.n_actions, max_size=self.buffer_size, device=self.device)

        # Build a tensorboard
        self.writer = SummaryWriter(log_dir='runs/DDPG_{}'.format(datetime.datetime.now().strftime('%Y-%m-%d_%H-%M-%S')))

        # global planner
        g_start = (start[0], start[1])
        g_goal  = (goal[0], goal[1])
        self.g_planner = {"planner_name": "a_star", "start": g_start, "goal": g_goal, "env": env}
        self.path = self.g_path[::-1]

    def __del__(self) -> None:
        self.writer.close()

    def __str__(self) -> str:
        return "Deep Deterministic Policy Gradient (DDPG)"

    def plan(self) -> tuple:
        """
        Deep Deterministic Policy Gradient (DDPG) motion plan function.

        Returns:
            flag (bool): planning successful if true else failed
            pose_list (list): history poses of robot
        """
        s = self.reset()
        for _ in range(self.params["MAX_ITERATION"]):
            # break until goal reached
            if self.reach_goal(tuple(s[0:3]), tuple(s[5:8])):
                return True, self.robot.history_pose

            # get the particular point on the path at the lookahead distance to track
            lookahead_pt, theta_trj, kappa = self.getLookaheadPoint()
            s[5:7] = torch.tensor(lookahead_pt, device=self.device)
            s[7] = torch.tensor(theta_trj, device=self.device)

            a = self.select_action(s)   # get the action from the actor network
            s_, r, done, win = self.step(s, a)  # take the action and get the next state and reward
            s = s_  # Move to the next state
            self.robot.px, self.robot.py, self.robot.theta, self.robot.v, self.robot.w = tuple(s[0:5].cpu().numpy())

        return True, self.robot.history_pose
        # return False, None

    def run(self) -> None:
        """
        Running both plannig and animation.
        """
        _, history_pose = self.plan()
        print(f"Number of iterations: {len(history_pose)}")
        if not history_pose:
            raise ValueError("Path not found and planning failed!")

        path = np.array(history_pose)[:, 0:2]
        cost = np.sum(np.sqrt(np.sum(np.diff(path, axis=0)**2, axis=1, keepdims=True)))
        self.plot.plotPath(self.path, path_color="r", path_style="--")
        self.plot.animation(path, str(self), cost, history_pose=history_pose)

    def reset(self, random_sg: bool = False) -> torch.Tensor:
        """
        Reset the environment and the robot.

        Parameters:
            random_sg (bool): whether to generate random start and goal or not

        Returns:
            state (torch.Tensor): initial state of the robot
        """
        if random_sg:   # random start and goal
            start = (random.uniform(0, self.env.x_range), random.uniform(0, self.env.y_range), random.uniform(-math.pi, math.pi))
            # generate random start and goal until they are not in collision
            while self.in_collision(start):
                start = (random.uniform(0, self.env.x_range), random.uniform(0, self.env.y_range), random.uniform(-math.pi, math.pi))

            # goal is on the circle with radius self.params["MAX_LOOKAHEAD_DIST"] centered at start
            goal_angle = random.uniform(-math.pi, math.pi)
            goal_dist = self.params["MAX_LOOKAHEAD_DIST"]
            goal_x = start[0] + goal_dist * math.cos(goal_angle)
            goal_y = start[1] + goal_dist * math.sin(goal_angle)
            goal = (goal_x, goal_y, goal_angle)

            while self.in_collision(goal):
                goal_angle = random.uniform(-math.pi, math.pi)
                goal_dist = self.params["MAX_LOOKAHEAD_DIST"]
                goal_x = start[0] + goal_dist * math.cos(goal_angle)
                goal_y = start[1] + goal_dist * math.sin(goal_angle)
                goal = (goal_x, goal_y, goal_angle)

        else:
            start = self.start
            goal = self.goal

        self.robot = Robot(start[0], start[1], start[2], 0, 0)
        state = self.robot.state    # np.array([[self.px], [self.py], [self.theta], [self.v], [self.w]])
        state = np.pad(state, pad_width=((0, 3), (0, 0)), mode='constant')
        state[5:8, 0] = goal
        state = torch.tensor(state, device=self.device, dtype=torch.float).squeeze(dim=1)
        return state

    def step(self, state: torch.Tensor, action: torch.Tensor) -> tuple:
        """
        Take a step in the environment.

        Parameters:
            state (torch.Tensor): current state of the robot
            action (torch.Tensor): action to take

        Returns:
            next_state (torch.Tensor): next state of the robot
            reward (float): reward for taking the action
            done (bool): whether the episode is done
        """
        dt = self.params["TIME_STEP"]
        v_d = (state[3] + action[0] * dt).item()
        w_d = (state[4] + action[1] * dt).item()
        self.robot.kinematic(np.array([[v_d], [w_d]]), dt)
        next_state = self.robot.state
        next_state = np.pad(next_state, pad_width=((0, 3), (0, 0)), mode='constant')
        next_state = torch.tensor(next_state, device=self.device, dtype=torch.float).squeeze(dim=1)
        next_state[5:8] = state[5:8]
        next_state[2] = self.regularizeAngle(next_state[2].item())
        next_state[3] = MathHelper.clamp(next_state[3].item(), self.params["MIN_V"], self.params["MAX_V"])
        next_state[4] = MathHelper.clamp(next_state[4].item(), self.params["MIN_W"], self.params["MAX_W"])
        win = self.reach_goal(tuple(next_state[0:3]), tuple(next_state[5:8]))
        lose = self.in_collision(tuple(next_state[0:2]))
        reward = self.reward(next_state, win, lose)
        done = win or lose
        return next_state, reward, done, win

    def reward(self, state: torch.Tensor, win: bool, lose: bool) -> float:
        """
        The state reward function.

        Parameters:
            state (torch.Tensor): current state of the robot
            win (bool): whether the episode is won (reached the goal)
            lose (bool): whether the episode is lost (collided)

        Returns:
            reward (float): reward for the current state
        """
        reward = 0

        goal_dist = self.dist((state[0], state[1]), (state[5], state[6]))
        scaled_goal_dist = goal_dist / self.params["MAX_LOOKAHEAD_DIST"]

        reward -= scaled_goal_dist

        if win:
            reward += self.max_episode_steps
        if lose:
            reward -= self.max_episode_steps / 5.0

        return reward

训练与评估

由于我们的目标是让DDPG做路径跟踪，那么就要有个跟踪目标，代码里会实时计算智能体在路径投影上前方1.5~2.5m的跟踪目标点，具体可查看代码仓库的相关代码。

train函数的训练过程中，一开始的行为策略是采取随机行动来进行探索，episode超过了random_episodes之后，此时认为已经搜集到了足够的经验，可以开始训练目标策略，行为策略也会改为在目标策略上加随机噪声。

optimize_model函数是对两个神经网络进行更新，每调用一次它，会从经验回放缓存中随机采样batch_size个经验样本（一般batch_size越大训练效果越好，但计算代价也越高），然后更新Actor和Critic。这是更新步骤：

1. 抽取得到经验样本 $(s,a,r,a^{\prime },\text{win})$ ；
2. Actor预测经验样本下一个状态 $s^{\prime }$ 应采取的动作 $a^{\prime }$ ；
3. Critic对状态动作对 $(s,a)$ 进行评估，得到动作价值 $q$ ，对状态动作对 $(s^{\prime },a^{\prime })$ 进行评估，得到动作价值 $q^{\prime }$；
4. 计算TD目标 $\hat{y}=r+\gamma \cdot q^{\prime }$（如果 $\text{win}$ 为真， $\hat{y}=r$ ），计算TD误差 $\delta =q-\hat{y}$；
5. 更新Critic，Loss为TD误差 $\delta$ ，从而使Critic更接近真实的动作价值函数 $Q(s,a)$；
6. 更新Actor，Loss为Critic预测的 $q(s,a)$ 的负值，从而使Actor朝着高回报的动作优化（ ${\nabla }_{\theta }q(s,a)$ 也就是确定性策略梯度（Deterministic Policy Gradient，DPG）， $\theta$ 是Actor网络参数）。

这里用了目标网络来缓解高估问题，并用了软更新、梯度裁剪等tricks。先用目标网络计算TD目标，用这个TD目标更新原网络，再用原网络来软更新目标网络。

evaluate_policy函数用于评估当前Actor执行完整Episode得到的平均奖励，不更新模型，但得到的经验也会被收集用于后续训练。

    def select_action(self, s: torch.Tensor) -> torch.Tensor:
        """
        Select the action from the actor network.

        Parameters:
            s (torch.Tensor): current state

        Returns:
            a (torch.Tensor): selected action
        """
        s = torch.unsqueeze(s.clone().detach(), 0)
        a = self.actor(s).detach().flatten()
        return a

    def optimize_model(self) -> tuple:
        """
        Optimize the neural networks when training.

        Returns:
            actor_loss (float): actor loss
            critic_loss (float): critic loss
        """
        batch_s, batch_a, batch_r, batch_s_, batch_win = self.replay_buffer.sample(self.batch_size)  # Sample a batch

        # Compute the target q
        with torch.no_grad():  # target_q has no gradient
            q_ = self.critic_target(batch_s_, self.actor_target(batch_s_))
            target_q = batch_r + self.gamma * torch.logical_not(batch_win) * q_

        # Compute the current q and the critic loss
        current_q = self.critic(batch_s, batch_a)
        critic_loss = self.criterion(target_q, current_q)

        # Optimize the critic
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        torch.nn.utils.clip_grad_norm_(self.critic.parameters(), max_norm=1.0, norm_type=2)  # clip the gradient
        self.critic_optimizer.step()

        # Freeze critic networks so you don't waste computational effort
        for params in self.critic.parameters():
            params.requires_grad = False

        # Compute the actor loss
        actor_loss = -self.critic(batch_s, self.actor(batch_s)).mean()
        # Optimize the actor
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        torch.nn.utils.clip_grad_norm_(self.actor.parameters(), max_norm=1.0, norm_type=2)  # clip the gradient
        self.actor_optimizer.step()

        # Unfreeze critic networks
        for params in self.critic.parameters():
            params.requires_grad = True

        # Softly update the target networks
        for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

        for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

        return actor_loss.item(), critic_loss.item()

    def evaluate_policy(self) -> float:
        """
        Evaluate the policy and calculating the average reward.

        Returns:
            evaluate_reward (float): average reward of the policy
        """
        print(f"Evaluating: ")
        evaluate_reward = 0
        for _ in tqdm(range(self.evaluate_freq)):
            s = self.reset(random_sg=True)
            done = False
            episode_reward = 0
            step = 0
            while not done:
                a = self.select_action(s)  # We do not add noise when evaluating
                s_, r, done, win = self.step(s, a)
                self.replay_buffer.store(s, a, r, s_, win)  # Store the transition
                episode_reward += r
                s = s_
                step += 1
                if step >= self.max_episode_steps:
                    break
            evaluate_reward += episode_reward / step

        return evaluate_reward / self.evaluate_freq

    def train(self, num_episodes: int = 1000) -> None:
        """
        Train the model.

        Parameters:
            num_episodes (int): number of episodes to train the model
        """
        noise_std = self.train_noise * torch.tensor([
            self.params["MAX_V_INC"] - self.params["MIN_V_INC"],
            self.params["MAX_W_INC"] - self.params["MIN_W_INC"]
        ], device=self.device)  # the std of Gaussian noise for exploration

        best_reward = -float('inf')

        # Train the model
        for episode in range(1, num_episodes+1):
            print(f"Episode: {episode}/{num_episodes}, Training: ")
            s = self.reset(random_sg=True)
            episode_actor_loss = 0
            episode_critic_loss = 0
            optimize_times = 0
            for episode_steps in tqdm(range(1, self.max_episode_steps+1)):
                if episode <= self.random_episodes:
                    # Take the random actions in the beginning for the better exploration
                    a = torch.tensor([
                        random.uniform(self.params["MIN_V_INC"], self.params["MAX_V_INC"]),
                        random.uniform(self.params["MIN_W_INC"], self.params["MAX_W_INC"])
                    ], device=self.device)
                else:
                    # Add Gaussian noise to actions for exploration
                    a = self.select_action(s)
                    a[0] = ((a[0] + torch.normal(0., noise_std[0].item(), size=(1,), device=self.device)).
                            clamp(self.params["MIN_V_INC"], self.params["MAX_V_INC"]))
                    a[1] = ((a[1] + torch.normal(0., noise_std[1].item(), size=(1,), device=self.device)).
                            clamp(self.params["MIN_W_INC"], self.params["MAX_W_INC"]))
                s_, r, done, win = self.step(s, a)

                self.replay_buffer.store(s, a, r, s_, win)  # Store the transition

                # update the networks if enough samples are available
                if episode > self.random_episodes and (episode_steps % self.update_steps == 0 or done):
                    for _ in range(self.update_freq):
                        actor_loss, critic_loss = self.optimize_model()
                        episode_actor_loss += actor_loss
                        episode_critic_loss += critic_loss
                        optimize_times += 1

                if win:
                    print(f"Goal reached! State: {s}, Action: {a}, Reward: {r:.4f}, Next State: {s_}")
                    break
                elif done:  # lose (collide)
                    print(f"Collision! State: {s}, Action: {a}, Reward: {r:.4f}, Next State: {s_}")
                    break

                s = s_  # Move to the next state

            if episode > self.random_episodes:
                average_actor_loss = episode_actor_loss / optimize_times
                average_critic_loss = episode_critic_loss / optimize_times
                self.writer.add_scalar('Actor train loss', average_actor_loss, global_step=episode)
                self.writer.add_scalar('Critic train loss', average_critic_loss, global_step=episode)

            if episode % self.evaluate_episodes == 0 and episode > self.random_episodes - self.evaluate_episodes:
                print()
                evaluate_reward = self.evaluate_policy()
                print("Evaluate_reward:{}".format(evaluate_reward))
                print()
                self.writer.add_scalar('Evaluate reward', evaluate_reward, global_step=episode)
                self.writer.add_scalar('Learning rate', self.actor_scheduler.optimizer.param_groups[0]['lr'],
                                       global_step=episode)     # Learning rates of the actor and critic are the same

                self.actor_scheduler.step(evaluate_reward)
                self.critic_scheduler.step(evaluate_reward)

                # Save the model
                if evaluate_reward > best_reward:
                    best_reward = evaluate_reward

                    # Create the directory if it does not exist
                    if not os.path.exists(os.path.dirname(self.actor_save_path)):
                        os.makedirs(os.path.dirname(self.actor_save_path))
                    if not os.path.exists(os.path.dirname(self.critic_save_path)):
                        os.makedirs(os.path.dirname(self.critic_save_path))

                    torch.save(self.actor.state_dict(), self.actor_save_path)
                    torch.save(self.critic.state_dict(), self.critic_save_path)

训练曲线可视化

以下是默认参数下训练过程中一些重要数值变化的Tensorboard可视化曲线：

测试

测试的路径跟踪效果如下。

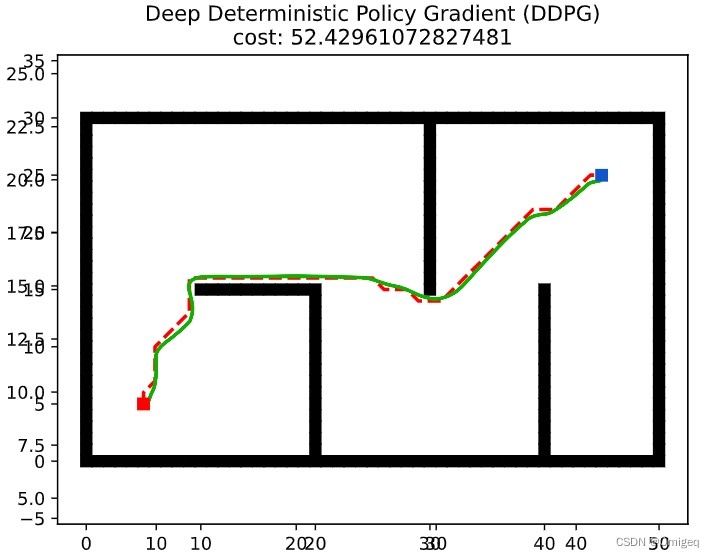
用DDPG训练的AI能控制智能体跟踪完A*规划的路径全程。总体效果不如传统路径跟踪算法，轨迹碰到了障碍物的一个角，终点处也明显有点偏差。

但DDPG等深度强化学习算法还是很有潜力的。算法还可以继续优化，我这个代码实现中，神经网络是深度3宽度512的MLP，更换神经网络结构有可能得到更好的结果，不过对算力的要求也会更高。经验回放缓存改成优先经验回放应该也会得到更好的训练效果。

至于实时性，我在本地进行了测试，每个step平均耗时0.02174532秒，而在仿真中设定的一个时间步长度为0.1s，所以在这个配置下是能够做到实时计算动作的。然而，如果换成更复杂的神经网络，计算消耗会更大，需要高配置服务器才能实时计算动作。