ANYA：一种最优任意角度在线2D寻路算法（论文解读+伪代码）

参考资料

[1] 原论文https://ojs.aaai.org/index.php/ICAPS/article/view/13609.
[2] 算法对比 http://idm-lab.org/bib/abstracts/papers/socs15a.pdf.
[3] 更详细介绍及伪代码实现 http://www.grastien.net/ban/articles/hgoa-jair16.pdf.

算法效果

了解一个算法，首先我们会关注算法效果，如果算法效果不好，我们就没什么必要花费宝贵的时间精力去学习它了。本文开头参考资料中第二篇论文给出了算法效果对比。柱形图中ANYA的值全为0，这个值是算法在地图中规划出的路径长度相比最优路径更长的比例。全为0意味着规划出的路径是最优路径。看来这个算法很值得了解一下。
当然，缺点也是有的，这个算法推理会比较慢。

算法简介

ANYA算法是一种用于任意角度路径规划的算法。ANYA算法的关键优势在于其能够在线处理查询，即不需要预先的数据处理步骤，且始终能够找到最优路径。

经典的任意角度路径规划算法有Theta*等，相比A*等算法，它们规划出来的路径角度不受地图的栅格限制，而且路径长度通常更短，很适合用于机器人和游戏中的路径规划，详情请参考维基百科。

传统的路径规划方法通常只考虑栅格上的离散点，并通过后处理步骤来优化路径长度和外观。然而，这些方法存在一些局限性：它们通常只能产生近似最短路径，并且在计算上更为复杂。

ANYA算法的主要创新在于它不是在单个栅格结点上进行搜索，而是在由连续状态集合形成的区间上进行搜索。每个区间都有一个代表性的点，用来推导出该集合的f值（即路径评估函数值）。这种方法的优势在于它无需预处理，不引入额外的内存开销，且总是能找到最优的任意角度路径。

相比A*家族的Theta*等算法，它采用了一种截然不同的思路。考虑到实现方式差异过大，ANYA并不能完全代替Theta*等算法，在具体情景中还要酌情进行算法选择。ANYA最基础的版本一般只适用于2D的且只有01两个状态(有无障碍物)的网格地图。在不均匀代价地图中，或者更高维地图等场景，还是A*和Theta*这些算法的变种学界研究得更深入一些。

具体来说，ANYA算法通过以下步骤实现路径规划：

• 定义区间（Interval）：区间是栅格上一连串可见点的集合，由两个端点定义。
• 寻找区间：算法在执行过程中动态地构建区间，从而可以立即开始回答查询。
• 定义搜索结点：搜索结点由一个区间和一个根点组成，其中每个区间中的点都可以从根点看见。
• 生成后继结点：算法计算同一栅格行及其相邻行上的可遍历点集合来识别后继结点。
• 评估和扩展结点：对于每个搜索结点，算法选择一个具有最小$f$值的点，并根据此点对搜索结点进行评估。

ANYA的状态空间由$(l,r)$形式的元组组成，其中$I$（Interval，区间）是沿网格行的一组连续点，$r$（root，根）是一个单元格角，因此任何点$p\in I$都可以从$r$中看到。当状态$(l,r)$扩展时，ANYA生成了$(I^{\prime },r^{\prime })$形式的后继者，其中$I^{\prime }$与$I$在同一行或相邻行， r ′ ∈ { r } ∪ I r' \in \{r\}\cup I r′∈{r}∪I。我们省略了状态后继者生成的确切细节。直观地说，ANYA确保对于任何状态$(l,r)$，$r$是从起点$s$到任何点$p\in I$的张紧路径2上的最新转折点。当扩展了包含目标的状态（目标状态）时，搜索终止。通过从目标状态到起始状态的父指针来提取路径。遇到的状态的根点是从起点到目标的最短任意角度路径上的转折点。ANYA使用启发式方法，估计状态$(l,r)$从$r$到目标经过任何点$p\in I$的最短距离。

具体内容

ANYA主要进行对比的是流行的启发式任意角度路径规划算法Theta*，如果没有接触Theta*算法建议先学习Theta*算法，当然，学习Theta*算法之前要学习更流行且更基础的A*算法与Dijkstra等算法，按顺序学习历史上重要的路径规划算法，才能帮助你更好地理解为什么这些算法要这么设计，它们都是在前人基础上设计改进而成的。Theta*也是一个很优秀的算法，但可能会陷入局部最优，而ANYA相比它能保证获得最优路径。

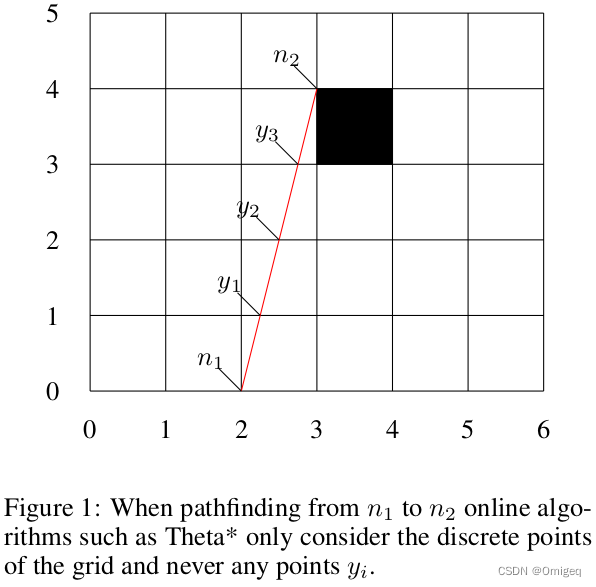
考虑图1中描述的任意角度实例。起点为$n_1=(2,0)$，目标点为$n_2=(3,4)$。解决此类问题的一种流行的在线算法是Theta*。这种方法仅考虑网格中的离散点集来计算任意角度路径。每次到达这样的点时，Theta*都会“拉弦”。因此，当生成结点$n_2$时，其$g$值不是从$n_1$到$n_2$的网格约束路径的长度，而是直接路径$<n_1,n_2>$的长度。

这种方法的问题在于，从父结点到其每个后继结点的解决方案成本估计（或$f$值）可能不是单调增加的。单调条件是保证总是找到最优解决方案（如果存在的话）的必要条件。例如：Theta*可以从中间点$p=(3,3)$生成$n_2$。当$p$扩展时，我们有$f(p)=d(n_1,p)+h(p,n_2)=4.16$。为了满足单调条件，我们需要$f(n_2)\ge 4.16$。然而，Theta*计算$f(n_2)=d(n_1,n_2)+h(n_2,n_2)=4.12$。显然，$p$应该在$n_2$之后扩展，但在这种情况下，情况正好相反。

为了避免这种错误，除了网格中的一组离散点外，我们还需要考虑图1中所示的所有点$y_i$。问题在于，这样的点的数量可能非常大：网格的每条边，连同其离散端点，形成一个$[0,1]$区间，可以在任何点$0\le \frac{w}{h}\le 1$处与最优路径相交；这里的$w$（或$h$）是$0,...,W$（或$0,...,H$）中的整数。这是一个其成员可归结为费里数列的集合。对于任何给定的$n$（在我们的例子中$n=max(W,H)$），相应元素集的基数已知为$n$的二次幂。因此，我们可以考虑另一种方法：我们不是单独评估每个$y_i$结点，而是将所有结点从每个$y_i$出现的相应区间中一起评估。

定义1 网格区间$I$是网格任何一行中一组连续的成对可见点。每个区间根据其端点$a$和$b$定义。除了$a$和$b$之外，每个区间只包含中间和离散的非角点。

确定区间很简单：网格的任何一行都可以自然地分为可遍历点和不可遍历点的最大连续集。每个可遍历集形成一个试验区间，我们反复分割，直到在$a$或$b$处找到唯一的角点。

Anya 的一个显著优势是我们可以动态构建区间。这使我们能够立即开始回答任何离散的起点-目标对查询。类似的算法（例如Continuous Dijkstra）在回答任何查询之前都需要一个预处理步骤，然后只能从一个固定的起点开始。

定义2 搜索结点$(I,r)$是一个元组，其中I是一个区间，$r\notin I$是一个选定的根点，使得每个$p\in I$都可以从$r$看到。$r$的标识始终是起点$s$到任何$p\in I$的路径上的最近转折点。为了表示起始结点，设置$I=[s]$，并假设$r$是一个位于平面外的点，只能从$s$看到。在这种情况下，从$r$到$s$的成本为零。

搜索结点$n$的后续结点是通过计算与$n$所在行和相邻行可遍历点集的区间来标识的。我们希望保证这样的集合中的每个点都可以通过一条局部路径从$n$的根结点到达。局部路径是 张紧（taut） 的。张紧意味着如果我们“拉动”路径的端点，我们无法使其变得更短。 张紧路径（taut path） 也是最短路径。“张紧”一词非常形象，可以想象为把固定在两端的橡皮筋拉紧，达到一个最短橡皮筋路径。

定义3 如果每个$p^{\prime }\in I^{\prime }$ 都可以通过一个从$r$开始并通过一些$p\in I$的张紧路径$<r,p,p^{\prime }>$到达，子路径$<p,p^{\prime }>$不与任何区间$J\ne I^{\prime }$ 相交（也就是$I$与$I^{\prime }$处于相邻行或同行），并且$r^{\prime }$是这些路径的最后一个共同点，则$(I^{\prime },r^{\prime })$是$(I,r)$的后继。

我们从从$r$到$I$可见的可遍历点集开始，并将该集划分为$0\le k$个相邻的封闭网格区间。我们将说每个这样的区间都是可观察的，并为每个区间生成相应的后继结点$(I^{\prime },r^{\prime })$，其根$r^{\prime }=r$。

并非所有后继者都是可被$r$观察的。例如，从$r$到$I$的张紧路径可以在区间$I$的端点$b$处相交，$b$也就是一个角点（corner point）。在这种情况下，我们得到一组可遍历点，这些点要么与$I$相邻，要么与可观察的后继者集合相邻。每个这样的点从$p=b$可见，但从$r$不可见。从这组不可见点中，我们构建了一个半开区间$I^{\prime }=[a^{\prime },b^{\prime })$ $s.t.$ $I^{\prime }$在最接近$b$的端点处是开放的。我们将$I^{\prime }$称为不可观察的，并生成相应的后继者$(I^{\prime },r^{\prime })$，根$r^{\prime }=b$。图2显示了可观察和不可观察的后继者的示例（橙色区间是可观察的，蓝色区间是不可观察的）。为了评估搜索结点$n=(I,r)$，我们选择一个点$p\in I$，该点对于根点$r$和目标点$t$具有最小$f$值。我们计算：$f(p)=g(r)+d(r,p)+h(p,t)$，其中$g(r)$是从起点到根的最佳路径的长度，$d(r,p)$是从$r$到$p$的直线距离，$h(p,t)$是一个可接受的启发式函数，一般由$h(p,t)=d(p,t)$即$p$和$t$的直线距离（忽略障碍）计算得到，它是从$p$到达$t$的成本下限。

由以下两个引理，可以确定点$p$。

引理1 设$t$和$r$为两个点，$I$为区间，则$I$的行在$t$和$r$的行之间。则$f$值最小的点$p\in I$为$I$中最接近$(t,r)$与$I$行的交点的点。

证明：如果$(t,r)$在$p_i$中与$I$相交，则$d(r,p)+h(p,t)$的最小值是$d(r,t)$，这是通过选择$p=p_i$（由三角不等式）获得的。否则，选择$p$作为$I$在$(r,t)$与$I$行相交的一侧的端点。

如果不满足引理1的前提条件，则可以通过$I$将$t$替换为其镜像版本$t^{\prime }$，这满足前提条件。

引理2 通过区间$I$的目标$t$的镜像点$t^{\prime }$满足$d(p,t)=d(p,t^{\prime })$，对于所有$p\in I$。

引理2是一个简单的几何结果。这两个引理在图3中都有说明。

当我们扩展结点$(I,r)$ $s.t.$ $t\in I$时，算法终止。根据引理1和2，该区间的$f$值保证相对于$t$是最小的。为了提取路径，我们只需遵循父指针，直到到达开始结点。与我们遇到的搜索结点相关的根点是$s$到$t$的最佳任意角度路径上的转折点。

为了证明正确性和最优性，我们证明了（i）最优路径出现在搜索空间中，并且（ii）当目标被扩展时，我们找到了最优路径。

定理1 对于出现在行上的任何点$p$，如果存在从$s$到$p$的最佳路径，则搜索树中存在一个结点对应于该路径。

证明：通过归纳法证明。考虑最优路径${\pi }_k=<p_1,...,p_k>$，其中$s=p_1$，$p_{k-1}$要么是与$p_k$隔一行的一个点（类似于图1中提到的$y_i$点），要么是同一行上的角点。通过归纳法，搜索树中有一个结点$(I,r)$表示到$p_{k-1}\in I$的最优路径。现在根据定义3，有一个结点$(I^{\prime },r^{\prime })$是$(I,r)$的后继结点，使得$p_k\in I^{\prime }$，而$r^{\prime }=r$，如果从$r$可以看到$p_k$，则$r^{\prime }=p_{k-1}$，该结点表示最优路径。

我们现在假设搜索空间是通过使用方程式（1）的A*搜索来探索的。

定理2 包含目标$t$的第一个扩展结点对应于到$t$的最佳路径。

证明：首先我们注意到结点的$f$值确实是区间所有结点中最小值，这意味着$f$是对目标实际成本的低估。其次，我们注意到，给定一个搜索结点$(I,r)$及其后继结点$(I^{\prime },r^{\prime })$，对于每个点$p^{\prime }\in I^{\prime }$，$p^{\prime }$的$f$值大于某些点$p\in I$的$f$值（如果$r^{\prime }\ne r$，则$p=r^{\prime }$ ；否则$p$是$I$和$(r,p^{\prime })$的交集）；因此$f$函数单调递增。最后，如果$t\in I$，搜索结点$(I,r)$的$f$函数是路径的长度。因此，表示$t$的次优路径的结点的$f$函数最终将超过最优路径距离，而表示最优路径的结点的$f$函数将始终保持在此值之下。

伪代码

先介绍下面的伪代码会出现的 锥结点（cone node） 和 平结点（flat node） 两个概念。

锥结点如下图，意思是根点$r$和区间$I$在不同行上。

平结点如下图，意思是根点$r$和区间$I$在同一行上。
Anya算法最关键最难写的是生成后继结点的部分，这是它的伪代码。

主函数就比较简单了。

实现

Python实现与ROS C++实现将于一个月内开源。