Numpy之ndarray进阶篇

前篇：Numpy之ndarray基础篇

堆叠操作

堆叠操作实质上就是把形状有相同之处的数组拼接起来。根据堆叠的方式可以分为横向堆叠hstack、竖向堆叠vstack、高度堆叠dstack和堆叠stack。这几个函数的主要参数都是包含要进行操作的维数相同的ndarray的元组，而stack还有额外的第二个参数axis。

vstack：将数组沿第一个维度堆叠。例如

该函数要求参数中的数组除第一个维度以外其他维度长度相同。

hstack：将数组沿第二个维度堆叠。

该函数要求参数中的数组除第二个维度以外其他维度长度相同。

dstack：将数组沿第三个维度堆叠。

该函数要求参数中的数组除第三个维度以外其他维度长度相同。

stack：添加一个新轴并将数组沿给定的轴堆叠。默认为0号轴。以二维数组为例：

上述结果可能看不出堆叠的方式，下面用散点图表示np.stack((a,b))的结果

可以看出其实是将两个数组叠在一起后将堆叠的那个轴作为给定的轴。下面是np.stack((a,b),axis=2)的结果：

由于a，b是二维数组，因此该结果和np.dstack((a,b))一样。

该函数要求参数中所有数组形状都相同。与之前的堆叠不同之处在于，它返回的数组维度总是比输入的多一个维度。

布尔索引与花式索引

Numpy的ndarray提供了与普通列表不同的索引方法，本质都是用一个含有索引信息的索引数组对ndarray中的数据进行索引。又由于ndarray可以进行逻辑运算来生成这些索引数组，这就使得ndarray能够自带普通列表没有的筛选功能。

布尔索引

布尔索引就是用一个由布尔值组成的数组来对ndarray数组进行索引。例如

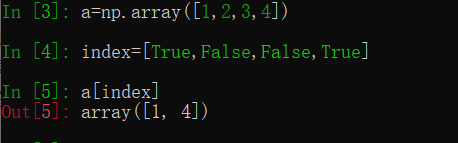
这将会返回索引数组中值为True的对应位置的元素。而在基础篇中已经介绍过，ndarray数组与基本类型变量/数值进行运算，将会返回依次运算的结果，因此可以用这个特性来生成布尔索引数组。

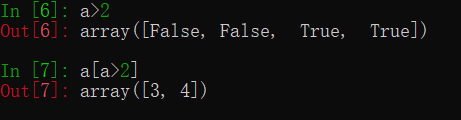
这样就实现了基本的筛选功能。还可以自定义更多筛选方法：

PS：注意上面的(a>5)&(a<14)括号不能漏，也不能用关键字and、or等联结，否则会报错。

花式索引

布尔索引是根据索引中布尔值来选出相应位置的元素，花式索引则是根据索引中的整数值来选出指定位置的元素。

这事实上提供了一种用已有数组构建新数组的简便方法，只需列出所需元素在已有数组中的索引即可。

广播机制

之前已经展示过，两个ndarray之间的相加、相乘等都是对应位置元素之间一次运算。如果两个ndarray形状不同，Numpy就会尝试将其中一个数组扩展成与另外一个相同形状。这种机制就叫广播(broadcasting)。

广播的原则：如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为1，则认为它们是广播兼容的。广播会在缺失或长度为1的维度上进行。
理解后缘维度的概念是理解广播的核心。简单来说，后缘维度相同就是要求其中一个数组的形状是另一个数组形状的后缀。例如，(1,2,3)和(2,3)后缘维度相同，(3,3,3)和(3,)后缘维度相同，而(2,3,3)和(3,3,3)后缘维度不相同。

广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为1。

例如以下代码

arr1=np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])	# arr1.shape=(2,2,3)
arr2=np.array([[1,0,0],[0,1,0]])						# arr2.shape=(2,3)
print(arr1*arr2)
"""结果为array([[[ 1,  0,  0],
        		 [ 0,  5,  0]],
       			[[ 7,  0,  0],
        		 [ 0, 11,  0]]])"""

上述运算过程中，由于arr1和arr2后缘维度相同（都为(2,3)），有缺失维度的arr2被广播成(2,2,3)形状的数组array([[[1,0,0],[0,1,0]],[[1,0,0],[0,1,0]]])，再与arr1进行元素依次相乘。

再如

arr1=np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])	# arr1.shape=(2,2,3)
arr2=np.array([[[1],[2]]])								# arr2.shape=(1,2,1)
print(arr1*arr2)
"""结果为array([[[ 1,  2,  3],
		         [ 8, 10, 12]],
       			[[ 7,  8,  9],
        		 [20, 22, 24]]])"""

上述运算过程中，arr1和arr2后缘维度中第一、三维虽不相同，但arr2的第一、三维长度为1，因此arr2被广播成(2,2,3)形状array([[[1,1,1],[2,2,2]],[[1,1,1],[2,2,2]]])。

线性代数运算

既然Numpy是提供科学计算的库，而且ndarray可以用来表示矩阵，那么Numpy自然也提供了矩阵相关的线性代数操作。常用函数如下：

函数	描述
dot	矩阵乘法
vdot	向量数量积
det	矩阵行列式
inv	方阵的逆
svd	奇异值分解
solve	解线性方程
matmul	矩阵积

dot(a, b, out=None)：参数a，b为要进行运算的两个ndarray对象，out为保存结果的ndarray对象。该函数返回俩个数组的点积。对于二维向量，效果等于矩阵乘法；对于一维数组，它是向量的内积；对于N维数组，它是a的最后一个轴上的数与b的倒数第二个轴的数乘积之和。

a=np.array([[1,2],[3,4]])
a1=np.array([[5,6],[7,8]])
np.dot(a,a1)
'''
输出：array([[19, 22],
       [43, 50]])
'''

linalg.det(a)：该函数用于计算输入矩阵的行列式。

a = np.array([[14, 1], [6, 2]])
a=linalg.det(a)
print(a)
'''
输出：21.999999999999996
'''

linalg.inv(a)：该函数用于计算方阵的逆矩阵。

 a=np.array([[1,2],[3,4]])
 b=linalg.inv(a)
 print(np.dot(a,b))
'''
输出：array([[1.0000000e+00, 0.0000000e+00],
       [8.8817842e-16, 1.0000000e+00]])
'''

linalg.solve(a, b)：该函数用于计算线性方程$Ax=b$的解。参数a即为系数方阵$A$，参数b为常数项矩阵$b$。

上图为求解线性方程组$\{\begin{array}{l}{x}_1+2x_2=2\\ 3x_1+4x_2=1\end{array}$和$\{\begin{array}{l}{x}_1+2x_2=2\\ 3x_1+4x_2=4\end{array}$，
求得解为$\{\begin{array}{l}{x}_1=-3\\ x_2=2.5\end{array}$和$\{\begin{array}{l}{x}_1=0\\ x_2=1\end{array}$。

matmul(x1, x2, out=None, **kwargs)：参数意义与dot类似。函数返回两个数组的矩阵乘积。如果参数中有一维数组，则通过在其维度上附加1来提升为矩阵，并在乘法之后去除。如果任一参数的维数大于2，则将其视为存在于最后两个索引的矩阵的栈，并进行相应广播。

a=[[3,4],[5,6]]
b=[[7,8],[9,10]]
np.matmul(a,b)
'''
输出：array([[ 57,  64],
       [ 89, 100]])
'''
b=[7,8]
np.matmul(a,b)
'''
b被升维成(2,1)的矩阵[[7],[8]]
输出：array([53, 83])
'''
np.matmul(b,a)
'''
b被升维成(1, 2)的矩阵[[7, 8]]
输出：array([57, 64])
'''
a=np.arange(8).reshape((2,2,2))
b=np.arange(4).reshape((1,2,2))
np.matmul(a,b)
'''
a=array([[[0, 1],
		  [2, 3]],
		 [[4, 5],
		  [6, 7]]])
b=array([[[0, 1],
		  [2, 3]]])
a被视为两个(2,2)矩阵的stack，b被认为一个(2,2)矩阵的stack。相乘时b广播为(2,2,2)形状，然后a的两个矩阵依次和b的两个矩阵做矩阵乘。结果为两个矩阵乘结果的stack
输出：array([[[ 2,  3],
	          [ 6, 11]],
       		 [[10, 19],
        	  [14, 27]]])
'''

svd(a, full_matrices=True, compute_uv=True, hermitian=False)：奇异值分解是一种矩阵分解的方法，该函数用来求解SVD。参数full_matrices为是否分解为方阵，compute_uv为是否将分解的矩阵相加，hermitian为指示a是否为厄密共轭的。

a=[[0,1],[1,1],[1,0]]
linalg.svd(a)
'''
输出:(array([[-4.08248290e-01,  7.07106781e-01,  5.77350269e-01],
       [-8.16496581e-01,  2.64811510e-17, -5.77350269e-01],
       [-4.08248290e-01, -7.07106781e-01,  5.77350269e-01]]), array([1.73205081, 1.        ]), array([[-0.70710678, -0.70710678],
       [-0.70710678,  0.70710678]]))
'''