Abstract
\qquad
温度的升高导致鱼群分布发生了显著的变化。苏格兰捕鱼业的主要猎捕对象为鲱鱼和鲭鱼,这种温度的上升可能会给苏格兰的捕鱼业带来毁灭性的打击,因为温度上升可能会导致鱼群的迁移。
\qquad
我们的团队被要求分析未来50年鲱鱼和鲭鱼的分布以及提出相应措施以缓解这种状况。
\qquad
对于问题一,我们首先分析过去100多年间海水的温度变化趋势,并基于此预测出未来50年内海水的温度变化趋势。我们采用了贝叶斯克里金插值法去清洗数据并使用支持向量机模型对数据进行拟合。我们得出的结论是未来50年内苏格兰岛附近气温大致会上升3-4℃。鲱鱼和鲭鱼将在未来50年内整体向北迁移。
\qquad
对于问题二,我们构建了区域鱼群密度模型,该模型受温度变化速率的影响,根据问题一中拟合的结果可以得到区域最大增长率,最小增长率以及平均增长率。我们设立密度阈值,当某区域的密度下降到最大密度的40%以下时,该地域便无法再进行捕捞。最终得到的结论是鲱鱼和鲭鱼最可能离开原捕鱼区域的时间分别为6.53年和6.93年。
\qquad
对于问题三,我们提出了两种策略以帮助苏格兰增加渔业收入。第一个策略为新建渔港,该策略可为苏格兰带来1.2亿英镑的额外净收入。第二个策略是一种新的捕鱼方式,一定比例的船只用作捕鱼而不返航,而另一部分的渔船负责运输鱼与供给燃料,这样的策略也可以增加苏格兰渔业的经济效益。
\qquad
对于问题四,我们考虑到领土主权和关税问题,我们采用Break-even模型讨论了不同情况下我们建议的修改与否,使得结论具有更广的使用范围。
\qquad
最后,我们对模型做了灵敏度分析,证明了模型的有效性和鲁棒性。
Introduction
\qquad
苏格兰岛是一个大型的捕鱼国家,捕鱼的效用很大一部分程度上取决于温度,因为温度会影响鱼群的分布。随着海洋温度的不断升高,苏格兰岛附近的鲱鱼和鲭鱼正在不断向适宜的地方迁移,如果任由这种趋势发展,那么在不久后苏格兰的经济将遭受巨大损失。
\qquad
本文的主要目的是帮助苏格兰渔业管理联盟制定有效的策略,从而扼制或减缓温度变化对捕鱼所带来的冲击。为了明确我们的分析,我们建立了数学模型对各因素进行量化。我们主要做了以下工作:
\qquad
1. 预测未来50年中全球海水温度的变化趋势,并由此指出鲱鱼和鲭鱼的大致迁徙路径。
\qquad
2. 明确鱼群迁移在当前捕捞点外的时间点,也即在原捕捞点无法继续捕捞的时间点。
\qquad
3. 提出建立新渔港和改变捕鱼方式两个方面去提高经济效率的捕鱼策略。
\qquad
4. 分析领土主权问题对捕鱼效益的影响。
Symbols
| 符号 | 意义 | 单位 |
|---|---|---|
| t t t | 时间 | 年 |
| p p p | 位置 | (纬度,经度) |
| T ( t , p ) T(t,p) T(t,p) | 温度 | ℃ |
| L 1 L O S S L1LOSS L1LOSS | L 1 L1 L1损失 | 1 |
| w w w | 超平面权重向量 | 1 |
| b b b | 超平面偏置 | 1 |
| g ( x ) g(x) g(x) | 超平面表达式 | 1 |
| L 1 L O S S c o r r e c t L1LOSS_{correct} L1LOSScorrect | 修正L1损失 | % |
| C ( T ) C(T) C(T) | 相对区域密度 | 1 |
1 Task1
1.1 数据处理
\qquad 本问题中,我们将考察未来50年鲱鱼和鲭鱼的迁移情况。虽然鱼的迁移受许多因素的影响,但此处为了简化模型同时抓住主要因素,我们只考虑海水温度的影响。
1.1.1 数据集
\qquad
我们使用了NOAA-SST数据集来拟合模型进而预测未来50年的海水温度变化趋势。该数据集是从全球海洋大气综合数据集(ICOADS)导出的全球月海表温度数据集,包含从88.0N-88.0S,0.0E-358E在内的从1800年开始到1967的月平均全球海洋表面温度。在空间上,SST数据集以2.0 degree latitude x 2.0 degree longitude 为单位,并通过以下手段改善了时空易变性:
\qquad
1. 减少训练重构函数的空间滤波经验正交遥相关(EOT)
\qquad
2. 消除EOTs中的高纬度阻尼
\qquad
3.在北极再增加10个EOTs,改善了SST的时空变异性
同时,第五版本的NOAA-SST数据集通过将夜间海洋气温(NMAT)作为参考值转换为buoy-SST作为矫正上版本NOAA-SST的参考值。
\qquad
基于这些数据,我们希望预测出海水温度随时空变化的数据。为了简化模型同时将连续问题转换为离散问题,我们对空间进行划分,规定以 2.0 degree latitude x 2.0 degree longitude 为空间单位进行划分(当然数据集中本身的处理即为此形式,这里再次提出是为了阐述我们处理问题的思路,当然我们也可以以 4.0 degree latitude x 4.0 degree longitude 或 8.0 degree latitude x 8.0 degree longitude 为单位进行划分)。经过这样的划分,我们将全球划分成了880个小格,去除246个陆地位置的小格,对剩余634个小格进行拟合分析。
\qquad
事实上海水温度的变化受许多复杂因素的影响(例如洋流、人类活动、日照时间等等)。该数据集中只给出了海水温度和地理位置(经纬度)和时间(月)的关系,同时也为了简化我们的模型,此处认为海水温度是关于地理位置和时间的映射关系。令
T
T
T为海水温度,则有:
T
=
T
(
t
,
p
)
(1-1)
T=T(t,p) \tag{1-1}
T=T(t,p)(1-1)其中
t
t
t为时间,
p
p
p为位置。
\qquad
尽管该数据集的收集者们已经对所收集数据做了详尽的处理,但我们仍需要进一步的处理。由于该数据集是以掩码矩阵形式存储数据的,为了方便处理,我们需要将其转换成普通矩阵的形式。数据中有少部分缺失值,产生这种缺失的原因有两种:
\qquad
1.某个地区处于陆地范围内,则该处温度缺失。
\qquad
2.某个地区处于海洋范围内,但未收集或对于该地收集结果置信度较低,则该处温度缺失
缺失的数据在原文件中统一以
−
9.36
-9.36
−9.36 x
1
0
36
℃
10^{36}℃
1036℃为填充值。这显然不符合事实,同时也会给我们的分析带来数值问题。基于此,我们对数据进行进一步的处理。
1.1.2 数据预处理与数据清洗
\qquad 数据预处理的主要目的是为了将数据处理成需要的格式(具体来说是模型能够处理的形式),数据清洗的主要目的是对数据进行过滤,内插或剔除异常值,对数据做相关的冗余分析等。对于本数据的处理步骤如下:
| 处理方法 | 目的 |
|---|---|
| 掩码矩阵转换 | 将数据转换为常见的格式,方便后续处理 |
| 数据缺失值处理 | 剔除数据中的异常值 |
\qquad
关于.nc文件与掩码矩阵的处理,我们可以借助Python中的第三方库netCDF4与numpy来实现。
\qquad
对于缺失值处理,我们提出以下策略。若该区域中的温度数据缺失比例达到
60
60%
60以上,则我们直接删除该区域的所有数据。否则,我们对区域数据的缺失值进行插值。为了评估不同的插值方法对该数据的适用程度,首先利用已知数据集对不同插值方法进行测试,并引入L1损失进行评估,L1损失定义如下:
L
1
L
O
S
S
=
1
N
∑
i
=
1
N
∣
y
−
y
p
r
e
d
i
c
t
∣
(1-2)
L1LOSS=\frac{1}{N}\sum_{i=1}^{N}|y-y_{predict}| \tag{1-2}
L1LOSS=N1i=1∑N∣y−ypredict∣(1-2)对损失进行修正,得到如下结果:
L
1
L
O
S
S
c
o
r
r
e
c
t
=
L
1
L
O
S
S
1
N
∑
i
=
1
N
∣
y
∣
∗
100
%
(1-3)
L1LOSS_{correct}=\frac{L1LOSS}{\frac{1}{N}\sum_{i=1}^{N}|y|}*100\% \tag{1-3}
L1LOSScorrect=N1∑i=1N∣y∣L1LOSS∗100%(1-3)结果如下:
| 插值方法 | L 1 L O S S c o r r e c t L1LOSS_{correct} L1LOSScorrect |
|---|---|
| 线性插值 | 72.34% |
| 二次插值 | 46.34% |
| 决策树插值 | 22.13% |
| 经验贝叶斯克里金插值 | 17.22% |
\qquad
根据上述结果,我们发现经验贝叶斯克里金插值(EBK)对该数据集拟合程度最好,故我们选用该方法去对缺失值进行处理。
\qquad
经验贝叶斯克里金插值法 (EBK) 是一种地统计插值方法,它通过估计基础半变异函数来说明所引入的误差。其他克里金方法通过已知的数据位置计算半变异函数,并使用此单一半变异函数在未知位置进行预测。该方法不仅被用过缺失值的插值,在预测问题方面也取得了较为广泛的应用,尤其在地理领域。其中的半异变函数定义如下:
γ
(
h
)
=
1
2
n
(
h
)
[
x
(
s
)
−
x
(
s
+
h
)
]
2
(1-4)
\gamma(h)=\frac{1}{2n(h)}[x(s)-x(s+h)]^{2} \tag{1-4}
γ(h)=2n(h)1[x(s)−x(s+h)]2(1-4)其中,s为样本点,x(s)为样本点s的属性值(在本例中即为温度),n(h)为距离为h的点对数。
\qquad
由图中可以看出距离越远,半变异函数值越大,说明两点间的属性相关性就越小;因此当距离越近,半变异函数值越小,相关性越大。当距离为0时,理论上半变异函数值为0,但由于误差的影响,其通常不为0。这恰好较为适宜用来反映温度与时间或位置的关系。
\qquad
结果EBK对部分缺失数据进行插值后,我们就得到了所有的预处理结果。下面我们将对这些数据建立拟合模型,从而预测未来50年海水温度的变化趋势。
1.2 未来海水温度预测
\qquad 在本部分,我们将基于上一部分处理得到的数据选取适宜的模型进行拟合,并使用此模型预测未来50年内海水温度的变化趋势。经验告诉我们,我们的数据应该是高度非线性的,同时我们需要找到预测误差最小的情况。基于此,我们使用支持向量机模型作为海水温度预测模型,并基于此进行鱼群迁移预测。
1.2.1 支持向量机模型
\qquad
原始SVM算法是由弗拉基米尔·万普尼克和亚历克塞·泽范兰杰斯于1963年发明的。1992年,Bernhard E. Boser、Isabelle M. Guyon和弗拉基米尔·万普尼克提出了一种通过将核技巧应用于最大间隔超平面来创建非线性分类器的方法。当前标准的前身(软间隔)由Corinna Cortes和Vapnik于1993年提出,并于1995年发表。

\qquad
如上图,最初的SVM分类算法要解决的问题是在多个线性分类边界中寻找到最优的一个分类边界,这使得在SVM算法的性能在深度学习出现之前一直遥遥领先。其公式如下:
M
a
x
(
r
)
=
w
T
x
i
+
b
∣
∣
w
∣
∣
(1-4)
Max (r)=\frac{w^{T}x_{i}+b}{||w||} \tag{1-4}
Max(r)=∣∣w∣∣wTxi+b(1-4)
s
.
t
.
y
i
(
w
T
x
i
+
b
)
=
γ
i
≥
γ
(1-5)
s.t. y_{i}(w^{T}x_{i}+b)=\gamma^{i}\geq\gamma \tag{1-5}
s.t.yi(wTxi+b)=γi≥γ(1-5)其中
w
w
w是超平面的法向量,
x
i
x_{i}
xi是超平面外任意一点,
r
r
r为该点到超平面的距离。该问题可根据对偶理论转换为以下问题:
max
w
,
b
θ
(
w
)
=
min
w
,
b
max
α
i
≥
0
L
(
w
,
b
,
α
)
(1-6)
\max\limits_{w,b}\theta(w)=\min\limits_{w,b}\max\limits_{\alpha_{i}\geq0}L(w,b,\alpha) \tag{1-6}
w,bmaxθ(w)=w,bminαi≥0maxL(w,b,α)(1-6)
L
(
w
,
b
,
α
)
=
1
2
w
T
w
+
∑
n
=
1
N
α
n
[
1
−
y
n
(
w
T
x
n
+
b
)
]
(1-7)
L(w,b,\alpha)=\frac{1}{2}w^{T}w+\sum\limits_{n=1}^{N}\alpha_{n}[1-y_{n}(w^{T}x_{n}+b)] \tag{1-7}
L(w,b,α)=21wTw+n=1∑Nαn[1−yn(wTxn+b)](1-7)
s
.
t
.
α
n
≥
0
(1-8)
s.t.\alpha_{n}\geq0 \tag{1-8}
s.t.αn≥0(1-8)利用拉格朗日乘数法,可以得到超平面的表达式:
g
(
x
)
=
(
∑
n
=
1
N
α
n
y
n
x
n
T
)
x
+
b
=
∑
n
=
1
N
α
n
y
n
<
x
n
,
x
>
+
b
(1-9)
g(x)=(\sum\limits_{n=1}^{N}\alpha_{n}y_{n}x_{n}^{T})x+b=\sum\limits_{n=1}\limits^{N}\alpha_{n}y_{n}<x_{n},x>+b \tag{1-9}
g(x)=(n=1∑NαnynxnT)x+b=n=1∑Nαnyn<xn,x>+b(1-9)
这便是最初的SVM形式,在后续又有学者提出了核方法支持向量机,将SVM推广到高度非线性问题上。
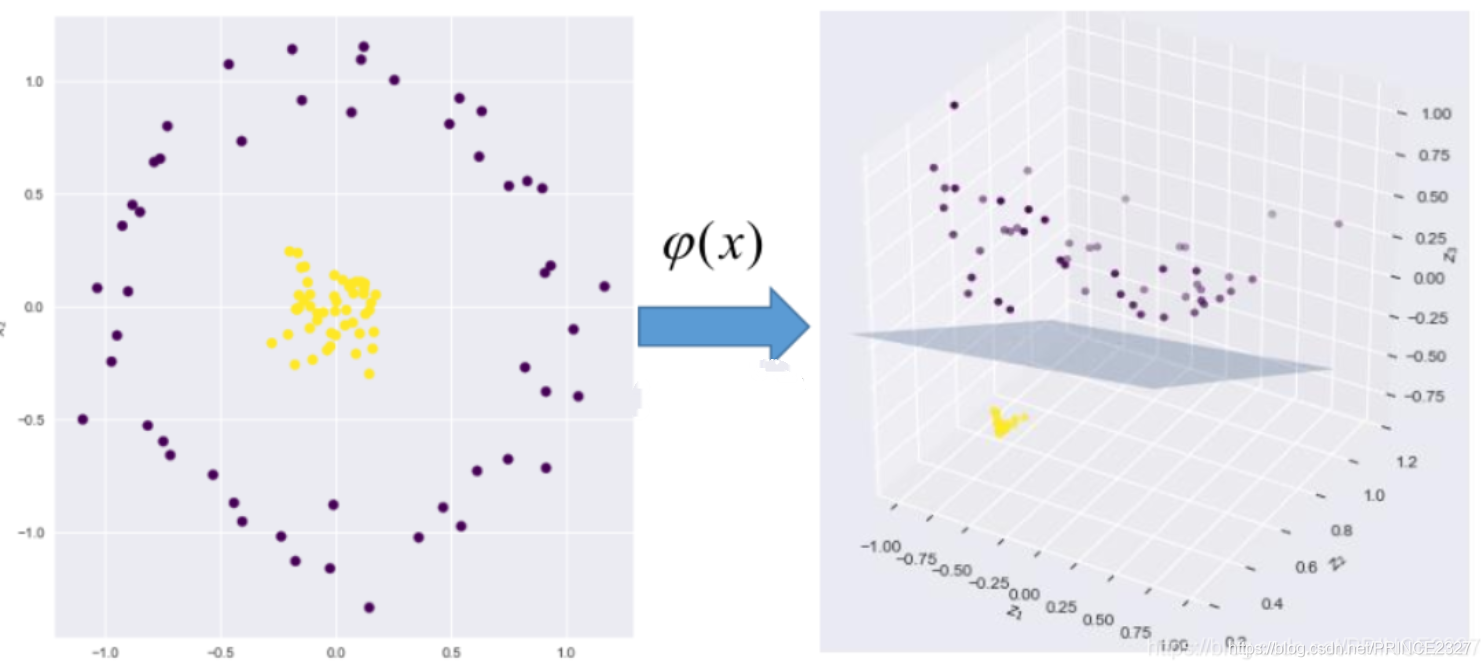

\qquad
如上图,核方法的基本思想建立在高维投影上,低维空间的非线性可分数据在高维空间上总是线性可分的。核方法利用这种思想以及特殊的数值计算方式,不仅解决了非线性问题,同时也减小了计算复杂度。
\qquad
在这之后,SVM被推广为SVR,原理同上述一样,只是转变为了回归问题。在本问题中,我们使用的便是SVR模型
1.2.2 海水温度拟合
\qquad
我们使用SVM中的SVR模型对数据进行拟合,考虑到数据的高度复杂以及高度非线性,我们选用高斯核作为核函数。得到如下预测结果:



\qquad 通过查阅资料可知,两种鱼的适宜温度大致如下:
| 种类 | 适宜温度(℃) | 最低忍受温度(℃) | 最高忍受温度(℃) |
|---|---|---|---|
| 鲱鱼 | 10.5 | 6.3 | 14.5 |
| 鲭鱼 | 7.0 | 4.2 | 9.2 |
基于以上数据及我们的模型拟合结果,我们可以得到未来50年内全球的海水温度变化以及两种鱼的分布趋势,如下图。
2020:

2030:

2050:
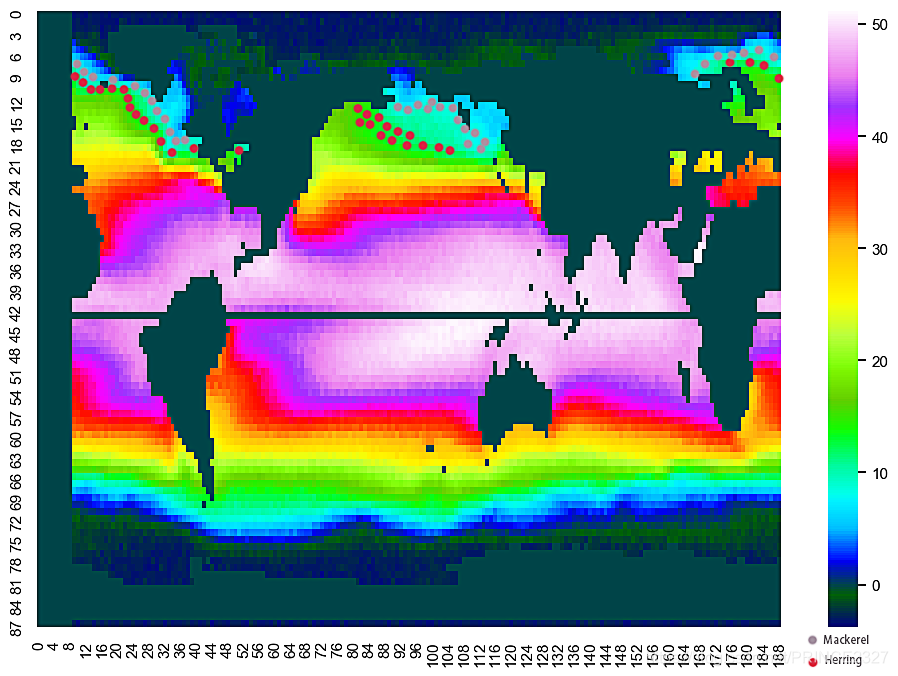
2070:
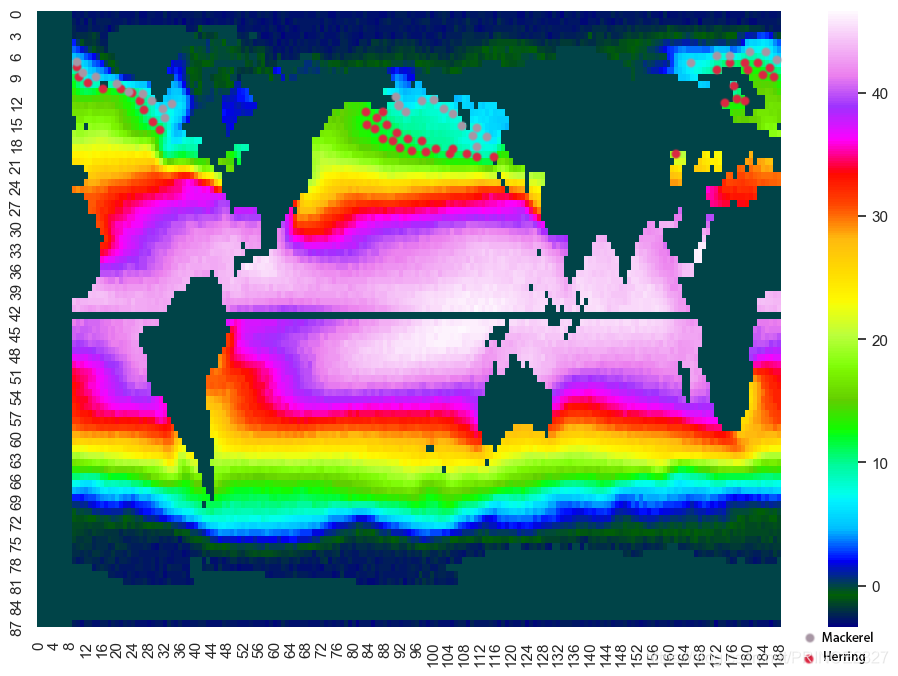
\qquad
两种鱼的迁移趋势如上图,可以看出,不论是鲱鱼还是鲭鱼,在足够长的时间内都会有朝北迁移的趋势,这是因为两种鱼主要分布在北半球并且随着时间的推移,低纬度区域的温度会渐渐升高,两种鱼为了满足自身生存的需要,会进行向高纬度区域的迁移,这也与事实相符。
2 Task2
\qquad 为了推断不同海洋温度变化速度下该渔港的经营状况,我们需要寻找渔港经营状况的主要影响因素。虽然渔港的经营状况受很多因素的影响(例如鱼的区域密度、洋流、经济波动、管理因素等等),但为了简化模型同时抓住主要因素,此处我们将鱼群密度建立为关于温度的函数,在此基础上,预测不同情况下渔港的经营状况。
2.1 鱼群密度推断模型
\qquad
第一个问题中我们已经获取了两种鱼的最适宜温度,最低忍受温度与最高忍受温度。我们建立如下的区域鱼群密度模型:
C
=
C
(
T
)
∈
[
0
,
1
]
(1-10)
C=C(T) \in [0,1] \tag{1-10}
C=C(T)∈[0,1](1-10)该密度模型被进行了归一化,最大值1表示该区域的鱼群密度为最适宜环境下的鱼群密度(也即最大密度),0表示该区域的鱼群密度为最恶劣环境下的鱼群密度(即没有鱼在此处生存)。根据第一问中的数据以及相关资料的查询,我们可以推断出如下结果。
Herry
| 温度(℃) | 区域相对密度 |
|---|---|
| 10.5 | 1 |
| 8.0 | 0.20 |
| 7.3 | 0.03 |
| 10.6 | 0.05 |
| 12 | 0.20 |
| 14 | 0.02 |
Mackerel
| 温度(℃) | 区域相对密度 |
|---|---|
| 7.0 | 1 |
| 8.0 | 0.30 |
| 9.2 | 0.03 |
| 6.0 | 0.28 |
| 5.0 | 0.10 |
| 4.2 | 0.01 |
\qquad 得到了基本的数据后,我们期望用拟合算法对离散点进行拟合,得到区域鱼群密度关于温度的具体表达式。我们选取了多种拟合方式进行拟合,得到如下的结果。
Herry
一次拟合

二次拟合
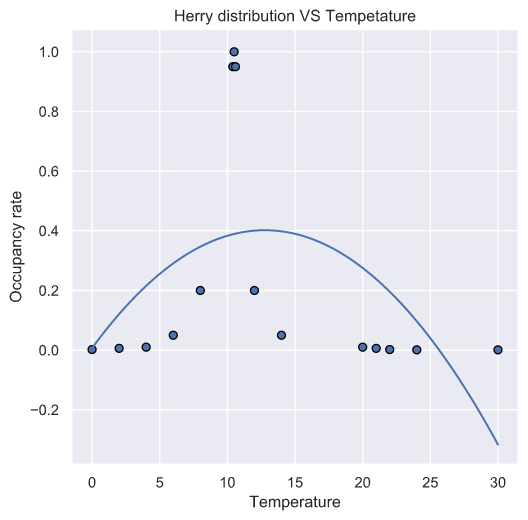
三次拟合

拉式插值

高斯拟合

Mackerel
一次拟合
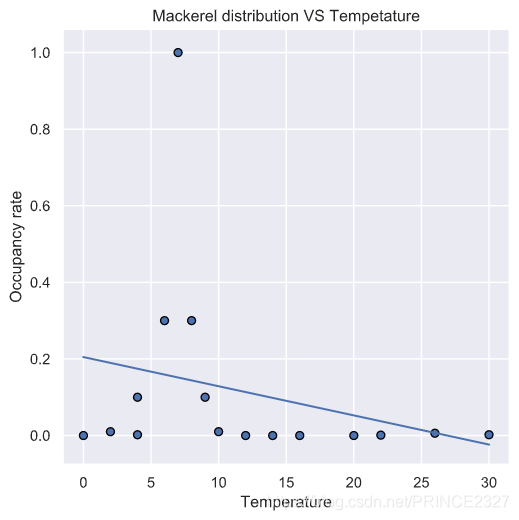
二次拟合

三次拟合

拉氏插值

高斯拟合

\qquad
可以看出,不论是鲱鱼还是鲭鱼,其区域密度与温度的关系用高斯分布拟合都是最优的。自然界中大多数的事物发展与因果规律都符合高斯分布,基于此,我们有理由相应该拟合结果的恰当性。
2.2 三种情况的推断
\qquad 2.1中我们已经建立了区域鱼群密度与温度的关系。在此基础上,我们需要分析不同的温度增长速度对区域密度的影响。在这里,我们基于任务1中的预测结果算出历年相对于上一年的平均水温增长率,并分别取最大值,最小值与均值作为三种情况的分界。
| 平均增长率(/年) | 最大增长率(/年) | 最小增长率(/年) |
|---|---|---|
| 0.005 | 0.009 | 0.003 |
\qquad 问题中说到当捕捞位置不变时,最多,最少和最可能继续捕鱼多长时间。由于捕捞位置不变,所以在此处我们选择2020年时最适宜捕捞的位置作为捕捞起始点,此时 C = 1 C=1 C=1,再考虑该处温度的不同变化以及对区域鱼群密度带来的影响。我们假设,当一个区域的鱼群密度下降到最适宜值的0.40以下时,出于密度系数或是生物保护等等的原因,渔港便无法再在此处继续捕捞,捕鱼公司也无法继续获得收益或持续经营。根据上述思路,可以得出如下结果。
Herry

Mackerel

根据上述分析,我们整理出如下结果。
| 鱼种类 | 最长时间(/年) | 最短时间(/年) | 最可能时间(/年) |
|---|---|---|---|
| 鲱鱼 | 11.00 | 3.66 | 6.53 |
| 鲭鱼 | 13.18 | 4.45 | 6.91 |
\qquad 按照本任务中的模型,我们可以得到如下结论:如果该公司的地点定在2020年的一个最适宜位置上,那么随着温度上升速度的不同,他们最终都会在14年后基本失去捕捞两种鱼的条件。基于此,我们将在任务3中讨论对于经营方式的改善方法,使得该渔港和捕鱼公司能够持续运转更长时间。
5 敏感性分析
\qquad
我们在任务2中建立了基于不同温度增长速率的经营情况预测模型,现在,我们略微修改先前所给出的水温增长率进而观察结论的变化。
\qquad
首先略微调高增长率,观察模型输出。
| 平均增长率(/年) | 最大增长率(/年) | 最小增长率(/年) |
|---|---|---|
| 0.008 | 0.013 | 0.006 |
Herry

Mackerel

| 鱼种类 | 最长时间(/年) | 最短时间(/年) | 最可能时间(/年) |
|---|---|---|---|
| 鲱鱼 | 6.53 | 4.13 | 5.52 |
| 鲭鱼 | 6.64 | 3.97 | 4.99 |
\qquad 在此基础之上,我们略微调低增长率再次观察模型输出。
| 平均增长率(/年) | 最大增长率(/年) | 最小增长率(/年) |
|---|---|---|
| 0.003 | 0.007 | 0.001 |
Herry

Mackerel

| 鱼种类 | 最长时间(/年) | 最短时间(/年) | 最可能时间(/年) |
|---|---|---|---|
| 鲱鱼 | 32.89 | 4.59 | 10.98 |
| 鲭鱼 | 6.64 | 3.97 | 4.99 |
\qquad 之后,我们大幅调高温度增长率,得到如下分析结果。
| 平均增长率(/年) | 最大增长率(/年) | 最小增长率(/年) |
|---|---|---|
| 0.009 | 0.015 | 0.005 |
Herry

Mackerel
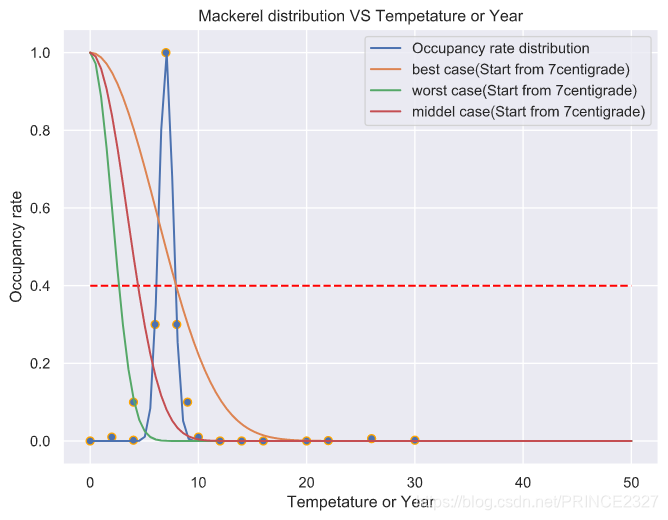
| 鱼种类 | 最长时间(/年) | 最短时间(/年) | 最可能时间(/年) |
|---|---|---|---|
| 鲱鱼 | 6.45 | 2.01 | 3.70 |
| 鲭鱼 | 7.96 | 2.64 | 4.32 |
\qquad 最后,我们大幅调低温度增长率,得到如下分析结果。
| 平均增长率(/年) | 最大增长率(/年) | 最小增长率(/年) |
|---|---|---|
| 0.002 | 0.003 | 0.001 |
Herry

Mackerel
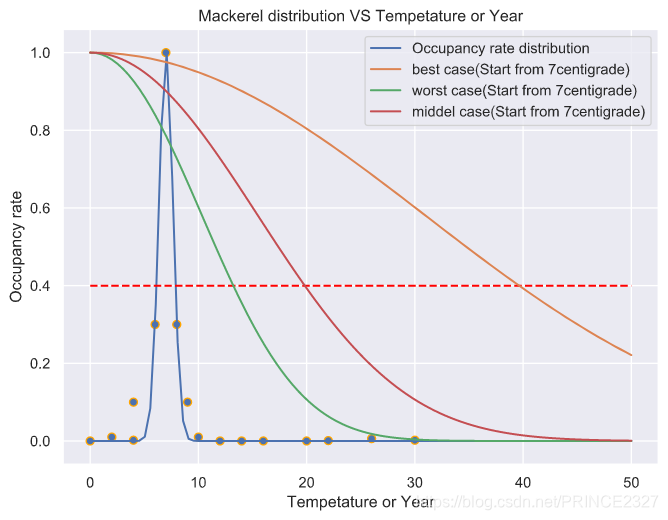
| 鱼种类 | 最长时间(/年) | 最短时间(/年) | 最可能时间(/年) |
|---|---|---|---|
| 鲱鱼 | 33.07 | 10.98 | 16.56 |
| 鲭鱼 | 39.72 | 13.19 | 20.11 |
\qquad
可以很明显地看出,我们的模型具有一定的鲁棒性,对于不同的初始参数,模型仍然可以给出较为合理的推断。即使初始参数发生大幅变化,模型也可以在一定范围内自适应地进行预测,而并不会产生不收敛的问题。除此之外,我们的模型也表现出一定的敏感性,即使是微小的初始参数变化,模型也可以检测到并对输出产生相应的改变。这也是符合实际的,在实际中,即使是微小的调整,在足够长的时间内也可以产生足够大的影响。综上所述,我们的模型具有足够的敏感性,但同时也保持一定的鲁棒性。
\qquad
根据上述分析,我们可以知道如果全球升温趋势得到有效扼制,那么在未来几十年内捕鱼业仍然可以维持原态继续发展。如果并不重视温室效应,放任其发展,那么在未来不到十年内便会失去在原位置上继续发展的条件。
优点和缺点
优点
1.正如敏感性分析中所指出的,我们的模型在一定程度上具有很高的敏感性,对于初始参数的细微变化也可以检测到并产生相应的合理输出。同时我们的模型也具有鲁棒性,对于噪声的干扰和初始参数的大幅改变,模型仍然可以保持较为合理的输出而不发散。
2.海水温度预测模型我们主要采用了SVM-SVR算法,该算法相对于其它算法的最大优点在于具有高度的非线性拟合能力与超高维拟合能力,同时在收敛时总是能找到最优或足够次优的回归超平面。
3.我们对缺失值的处理采用了剔除和插值两种方法,在保证去除异常值的同时最大程度保留了原数据中的大部分信息。
4.对于是否进行新建渔港的决策,我们采用了NPV模型,该模型考虑了资金的时间价值。
缺点
1.在进行海水温度变化预测时,我们只考虑了位置和时间两个因素的影响,事实上海水温度与洋流,人类活动等因素也有关。
2.在预测鱼群迁移趋势时,我们仅考虑了距离与温度适宜度两个因素的影响,事实上鱼群的迁移还受许多复杂因素的影响。























 1282
1282

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








