《数值计算》学习笔记（下）

Chp7 多项式计算

7.1 引言

一般的实系数n次多项式可以表示为
A(x)=a0+a1x+…+an-1xn-1+anxn
其中ak称为k次项的系数，k=0，1，…，n。
为了强调求A(x)是真正的n次多项式，也可以把A(x)记为An(x)，在这种情况下，总是假定an≠0。
若n=0而an≠0，则称A(x)为零次多项式，此时A(x)成为非零常数。
若A(x)≡0，则称之为-1次多项式。

7.2 多项式的基本计算

多项式的乘法
一般地，设A(x)，B(x)是两个次数分别为n，m的多项式，记C(x)=A(x)B(x)
那么C(x)是一个m+n次的多项式，通过B的每一项乘以A的每一项，按次数对齐合并同类项即可得到。
求两个多项式的积的C语言函数可说明为
int PolyMul(doubleA,doubleB,double*C,int n,int m)
其中：A，B，C分别为存放多项式A(x)，B(x)，C(x)的系数数组；n，m分别为多项式A(x)，B(x)的次数；函数返回值为零表示计算没有错误。

//程序7.01 多项式乘法运算
int PolyMul(double*A,double*B,double*C,int n,int m)
{ int i,j,k;
  for(j=0;j<=m+n+1;j++)C[j]=0.0;
  for(i=0;i<=m;i++)
     for(j=0;j<=n;j++)
     C[i+j]+=B[i]*A[j];
  return 0;
}

实例：

多项式带余除法
设A(x)，B(x)为两个已知的多项式，A(x)除以B(x)可以表示为

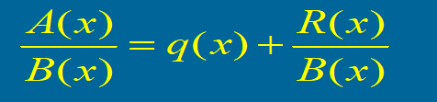
其中q(x)称为商式，R(x)称为余式。
约定余式的次数一定比除式B(x)的次数低。
一般情况下可以假定A(x)的次数一定不低于B(x)的次数，否则商式q(x)恒为零。

记号：若A(x)除以B(x)得到商式q(x)和余式R(x)，则有A(x)=q(x)B(x)+R(x)
约定：如果将多项式A(x)表为q(x)B(x)+R(x)的形式，则自动认为q(x)为A(x)除以B(x)所得的商式，R(x)为A(x)除以B(x)所得的余式。

int PolyDiv(double*A,double*B,double*R,int n,int m)
{ int i,j,k;
  if(n <m) return 1;
  for(j=0;j<=n;j++)R[j]=A[j];
  for(i=n;i>=m;i--)
  { R[i]/=B[m];
    for(j=1;j<=m;j++)R[i-j]-=R[i]*B[m-j];
  }
  return 0;
}

实例：

Chp8 线性方程组求解

8.1 线性方程组概述

对于一般形式的线性方程组而言,我们总可以假定它的系数矩阵或者满行秩,或者满列秩（线性无关）。在上面的假定下,我们有:
如果m<n,那么方程组有无数组解,我们通常要找某种意义下的最优解,这是运筹学中的线性规划就是专门研究这个问题；
如果m>n;那么方程组无解,此时作为实际问题还是有意义的,在求近似解我们可以转向求它的最小二乘解；
如果A是满秩的n阶方阵,那么方程有唯一解。

8.2 高斯消去法

高斯消去法解线性方程组其实就是中学里学过的加减消元法.它包括两个过程:首先把线性方程组化为上三角形线性方程组,接下来再用一个回代过程求这个上三角形线性方程组的解。
在所有的算法中,高斯消去法的计算量最小,所以是手工求解或利用计算器求解的首选方法。事实上也是求解一般问题的主流方法。

定义:如果线性方程组Ax=b的系数矩阵A是上三角形矩阵,则称为是上三角形线性方程组.
结论:上三角形线性方程组Ax=b有唯一解,也就是上三角形矩阵A可逆的充要条件是akk≠0,k=1,2,…,M.

实例：

//程序8.03A 化为上三角线性方程组
ToTriangle()
{ int i,j,k;  double x;
   for(k=0;k<RM;k++)
  { x = A[k][k];
    for(j=k;j<RN;j++)A[k][j] /= x;    
    if(k==RM-1)break;
    for(i=k+1;i<RM;i++)
    { x=A[i][k];
      for(j=k;j<RN;j++)
      A[i][j] -= x*A[k][j];
}
} 
return;}

//程序8.04A求解上三角形线性方程组
Void SolutionTriangle()
{ int I,j,k
  for(k=M-1;k>0;k--)
  for(i=0;i<k;i++)
  { A[i][N-1] -= A[i][k]*A[k][N-1];
    A[i][k]=0.0;
  }
  return;
}
//提示:循环体内增加一条语句“A[i][k]=0.0”可使得调试程序时所显示的结果更漂亮些。

8.3 选主元高斯消去法

选列主元方法
无论是高斯消去法还是约当消去法，我们都可以选列主元进行消元。
假如算法进行到第K步,选列主元的方法可表述为:
-找出aKK,aK+1K,…, aNK中绝对值最大的aMK;
-把第K个方程和第M个方程的位置互换；

实例：

//程序8.05A 选列主元算法的实现
GetMainElement(int k)
{ int i0,i;
  double temp0,temp;
  i0=k;
  temp0=fabs(A[k][k]);
  for(i=k+1;i<RM;i++)
  { temp=fabs(A[i][k]);
    if(temp<=temp0)
        continue;
    i0=i;
    temp0=temp;
  }
for(i=k;i<RN;i++)
{ temp=  A[k][i];
    A[k][i]=A[i0][i];
    A[[i0][i]=temp;
  }
  return;
} 
//注释:第一个循环查找主元所在的行号；第二个循环实现相应的两行互换.

8.4 高斯消去法应用模块的编写

解线性方程组在科学计算领域有着广泛的应用，所以单独在一个程序文件中独立编写一个解线性方程组的函数有应用程序调用是合适的。
一般说来，模块程序应该处理得便于“用户”使用，所以我们可以把这个函数说明为
double SolutionLEG(doubleP,doubleX,int m)
其中：
P为存放增广矩阵的首地址；
X为存放结果的首地址；
m为方程的个数，也是变量的个数。
函数的返回值处理为X的模是很实用的。

8.5 高斯-约当消去法

前言：
高斯消去法的的关键是把线性方程组化为上三角形线性方程组,也就是利用aK K不为零来消去aK+1,K,…,aN,K,不急于消去a1,K,…,aK-1,K仅仅是为了减少计算量,并非一定要留下一个回代过程.
结论,我们当然可以利用aK K不为零来同时消去a1,K,…,aK-1,K,方法与消去aK+1,K,…,aN,K是类似的,从而可以免去回代过程.
牢记:如果aK K不为零,我们可以从第K个方程中解出xK从而可以从其它方程中消去xK,这就是高斯-约当消去法的核心思想.

算法说明:
对I=1,2,…,M:
将第I个方程两边同时除以xI项的系数aII;;
对J=1,…,M:
A.if(J==I),continue;
B.方程(J)-=[方程(I)]* aI K;
选主元的考虑:在约当消去法中,我们也可以采用选主元的方法增强算法的可靠性,具体操作与高斯消去法相同.
计算量的估计:
第K步计算量为:M·(M+1-K)=O(M2-MK+M)=O(M2)
总计算量为:O(0.5M3)

实例：

//程序8.08 选列主元高斯-约当消去法
int Jordan()
{ int i,j,k;
  double x,test=0;
  if(SetPrintMatrix) PrintMatrix();
  for(k=0;k<PM;k++)
  { test=GetMainElement(k);
    if(SetPrintMatrix) PrintMatrix();
    if(test<ZERO){return k+1;}
    x = PA[k][k];
    for(j=k;j<PN;j++)PA[k][j] /= x;
    if(SetPrintMatrix) PrintMatrix();
    for(i=0;i<PM;i++)
    { if(i==k) continue;
      x=PA[i][k];
      for(j=k;j<PN;j++)
      PA[i][j] -= x*PA[k][j];
} }}

两个算法的对比分析
计算量:高斯消去法为O(0.33N3),约当消去法为O(0.5N3),从现代的观点看,两者的数量级相同；
算法简单:约当消去法占优；
通用性: 约当消去法占优；
数值稳定性:约当消去法更易于解决.
结论:如果用手工或计算器求解线性方程组（比如应付考试）,用高斯消去法较好,如果编程用计算机求解线性方程组,则用约当消去法更好.

Chp9 最小二乘法与曲线拟合

9.1 线性函数拟合方法

求解正规方程
矛盾方程 Xa=y
正规方程

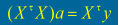
实例：写出正规方程并求解

9.2 最小二乘法

设有线性方程组
Xa=Y (1)
其中a是方程组的未知向量,且

在一般情况下，n>m,X是满列秩的矩阵，方程组无解。最小二乘法简单说来就是求（1）的尽可能准确的解的数学方法。

定义n+1维向量ε=(ε0,ε1,…,εn)T,令
ε= Xa-Y （2）
我们可以把 ε看作是用y近似表示Xa的误差向量。
思路：如果能找到a,使得ε为零向量，那么a就是（1）的准确解；如果a使得ε非常接近零向量，那么a就是（1）的很好的近似解。
为了度量这种接近的程度，我们将（2）两边左乘以各自的转置向量得
εT·ε= (Xa-Y)T·(Xa-Y) （3）
整理后即得 εT·ε= aT(XTX)a-2aTXTY+yTY
注意到εT·ε就是ε各项的平方和，我们可用它来评价ε接近零的程度。

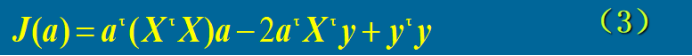
利用数学分析中的多变量函数取极值的必要条件（在我们这里也是充分条件）可以推出（3）的最优解也就是正规方程

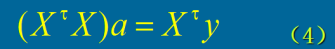
的解，我们称之为（1）的最小二乘解。
我们把求一个线性方程组的最小二乘解的方法称为最小二乘法。

第一步：在方程组（1）两边分别左乘以系数矩阵X的转置矩阵即可得到正规方程（4）；
第二步：求解正规方程组（4）；
第三步：检验解的有效性，也就是把（4）的解代入到（3）中计算出相应的J(a)，从而可进一步得到（标准差）sqrt(J(a)/n)。