T1:问题 B: 最大整数
题目描述
设有 n 个正整数(n≤20),将它们联接成一排,组成一个最大的多位整数。
例如:n=3 时,3 个整数 13,312,343 联接成的最大整数为:34331213
又如:n=4 时,4 个整数 7,13,4,246 联接成的最大整数为:7424613
输入
第一行一个整数,表示n;
第二行n个整数,之间用一个空格隔开。
输出
一行一个整数,表示联接成的最大多位数。
样例输入
3
13 312 343
样例输出
34331213
题解
或许各位有不同的算法,但是基本思想是相同的。即用贪心的方法,找到一种策略,然后从小到大输出答案即可。关键在于如何比较。我们来思考,如果只有2个数,该如何拼?最朴素的思想:比一比吧。假设有两个数a,b。凭感觉不好比,就试一试。先把a拼到b后面,再把b拼到a后面,最后比一比大小,就可以决定a,b哪个在前,哪个在后。运用这种思想,只要在排序的要求中按照这种方式排序,最后得到的一定是正确答案(此处不再详细解释)。那么有没有一种简单的方法搞定上述算法??很简单,用string即可。后面请欣赏简短的代码!
参考代码
#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
string s[590];int n;
bool comp1(string a,string b)
{
return (a+b)>(b+a);
}
int main()
{
int n;scanf("%d",&n);
for(int i=1;i<=n;i++)
cin>>s[i];
sort(s+1,s+n+1,comp1);
for(int i=1;i<=n;i++) cout<<s[i];
return 0;
}T2:问题 C: Hanoi 双塔问题
题目描述
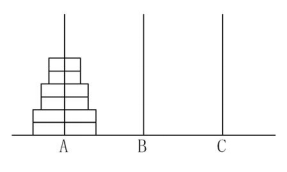
给定 A、B、C 三根足够长的细柱,在 A 柱上放有 2n 个中间有孔的圆盘,共有 n 个不同的尺寸,每个尺寸都有两个相同的圆盘,注意这两个圆盘是不加区分的(下图为 n=3 的情形)。现要将这些圆盘移到 C 柱上,在移动过程中可放在 B 柱上暂存。要求:
(1)每次只能移动一个圆盘;
(2)A、B、C 三根细柱上的圆盘都要保持上小下大的顺序;
任务:设An为 2n个圆盘完成上述任务所需的最少移动次数,对于输入的n,输出An。
输入
一行一个正整数 n,表示在 A 柱上放有 2n 个圆盘。
输出
仅一行,包含一个正整数, 为完成上述任务所需的最少移动次数An。
样例输入
2
样例输出
6
提示
【限制】
对于50%的数据,1<=n<=25
对于100%的数据,1<=n<=200
【提示】
设法建立An与An-1的递推关系式。
题解
很好证明,n盘普通汉诺塔的最小移动次数为2的n次方减1,这一点很好证明。
证明如下:
第n盘的最小移动次数与第(n-1)盘的最小移动次数息息相关。因为:先把上面(n-1)盘移到b,在用1次移到c,再用(n-1)盘的最小次数将b盘上的(n-1)盘全部移到c盘,就能完成n盘的转移。因此推出转移公式:dp[i]=2dp[i-1]+1。
然后用数列的基本方法就能轻易得出上述通项公式。
现在来看看与本题的关系。本题把原本的1盘变成了2盘,但是有一个限定条件是这两个盘一样,因此完全可以把2个盘合并成一个盘,只不过次数变成了原来的2倍(此处证明参照上述证明)。所以这道题就结束了。
注意数据范围,要打高精,我用的递推公式,所以只写了高精加。
参考代码
#include<cstdio>
using namespace std;
int p[1000000],q[1000000],z[1000000];
void add(int a[],int b[],int c[],int d[])
{
if(a[0]>b[0]) c[0]=a[0]+1;
else c[0]=b[0]+1;
for(int i=1;i<=c[0];i++)
{
c[i]=a[i]+b[i];
c[i+1]+=c[i]/10;
c[i]%=10;
}
while(c[c[0]]==0) c[0]--;
for(int i=0;i<=c[0];i++) d[i]=c[i];
}
int main()
{
int n;
scanf("%d",&n);
if(n==1) printf("2");
else
{
p[0]=p[1]=q[0]=q[1]=z[0]=z[1]=1;
for(int i=2;i<=n;i++)
{
add(p,q,p,p);//2倍
add(p,z,p,q);//加1
}
add(p,q,p,p);
for(int i=p[0];i>=1;i--)
printf("%d",p[i]);
}
return 0;
} T3:问题 D: Huffman编码树
题目描述
构造一个具有n个外部节点的扩充二叉树,每个外部节点Ki有一个Wi对应,作为该外部节点的权。使得这个扩充二叉树的叶节点带权外部路径长度总和最小:
Min( W1 * L1 + W2 * L2 + W3 * L3 + … + Wn * Ln)
Wi:每个节点的权值。
Li:根节点到第i个外部叶子节点的距离。
编程计算最小外部路径长度总和。
输入
第一行输入一个整数n,外部节点的个数。第二行输入n个整数,代表各个外部节点的权值。
2<=N<=100
输出
输出最小外部路径长度总和。
样例输入
4
1 1 3 5
样例输出
17
题解
这道题就是考合并果子。由于是2叉数,必然会有很多叶子节点。现在来考虑一下这个路径长度总和的公式:叶子节点会连续被算很多次。联系合并果子合并的过程,就是找2堆较小的叶子合并成一个叶子,并且ans+=该叶子的值。这样下去往上合并多少次,最小层的叶子就被重复加了多少次,以此类推,每次选择值最小的两个叶子合并,最后一定能组成一棵树。如果实在没有想到合并果子,就老老实实用优先队列的特殊operator尝试着做(虽然我直接编译错误~)。
参考代码
#include<cstdio>
#include<queue>
using namespace std;
priority_queue<int>q;
int n,a[300],ans=0;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int k;scanf("%d",&k);
q.push(-k);
}
while(q.size()>1)
{
int hr=-q.top();q.pop();
int ct=-q.top();q.pop();
ans+=hr+ct;
q.push(-(hr+ct));
}
printf("%d",ans);
return 0;
}T4:问题 E: 最短路径问题
目描述
平面上有n个点(n< =100),每个点的坐标均在- 10000~ 10000之间。其中的一些点之间有连线。
若有连线,则表示可从一个点到达另一个点,即两点间有通路,通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径。
输入
共n+m+3行,其中:
第1行为整数n。
第2行到第n+1行(共n行) ,每行两个整数x和y,描述了一个点的坐标。
第n+2行为一个整数m,表示图中连线的个数。
此后的m行,每行描述一条连线,由两个整数i和j组成,表示第i个点和第j个点之间有连线。
最后一行:两个整数s和t,分别表示源点和目标点。
输出
仅-行,一个实数(保留两位小数) ,表示从s到t的最短路径长度。
样例输入
5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5
样例输出
3.41
题解
标准的求最短路。用dj或者SPFA都可以。注意距离要处理成浮点,并且最后答案保留2位。
参考代码(SPFA)
#include<cstdio>
#include<cmath>
#include<queue>
#include<cstring>
using namespace std;
struct tree
{
int nxe,to;
double dis;
}tr[30000];
int head[30000],cnt=0;
int n,m,st,ed,vis[42200];
double x[42020],y[42020],d[42020];
queue<int>q;
void build_tree(int u,int v,double d1)
{
tr[++cnt].nxe=head[u];
tr[cnt].to=v;
tr[cnt].dis=d1;
head[u]=cnt;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&x[i],&y[i]);
d[i]=707406378.0;
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
build_tree(u,v,sqrt(double(x[u]-x[v])*double(x[u]-x[v])
+double(y[u]-y[v])*double(y[u]-y[v])));
build_tree(v,u,sqrt(double(x[u]-x[v])*double(x[u]-x[v])
+double(y[u]-y[v])*double(y[u]-y[v])));
}
scanf("%d%d",&st,&ed);
d[st]=0;
vis[st]=1;
q.push(st);
while(!q.empty())
{
int hr=q.front();q.pop();
vis[hr]=0;
for(int i=head[hr];i;i=tr[i].nxe)
{
int to=tr[i].to;
if(d[to]>d[hr]+tr[i].dis)
{
d[to]=d[hr]+tr[i].dis;
if(!vis[to])
{
vis[to]=1;
q.push(to);
}
}
}
}
printf("%.2lf",d[ed]);
return 0;
}参考代码(DJ)
#include<cstdio>
#include<cmath>
#include<queue>
#include<cstring>
using namespace std;
struct tree
{
int nxe,to;
double dis;
}tr[30000];
int head[30000],cnt=0;
int n,m,st,ed,vis[42200];
double x[42020],y[42020];
double dis[42020];
struct node {
double dis;int num;
};
priority_queue<node>q;
bool operator < (node a,node b) {
return a.dis>b.dis; }
void build_tree(int u,int v,double d1)
{
tr[++cnt].nxe=head[u];
tr[cnt].to=v;
tr[cnt].dis=d1;
head[u]=cnt;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&x[i],&y[i]);
dis[i]=707406378.0;
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
build_tree(u,v,sqrt(double(x[u]-x[v])*double(x[u]-x[v])
+double(y[u]-y[v])*double(y[u]-y[v])));
build_tree(v,u,sqrt(double(x[u]-x[v])*double(x[u]-x[v])
+double(y[u]-y[v])*double(y[u]-y[v])));
}
scanf("%d%d",&st,&ed);
node pt;dis[st]=0;
pt.dis=0.0;pt.num=st;
q.push(pt);
while(!q.empty())
{
node ttt=q.top();q.pop();
int nus=ttt.num;
if(vis[nus]) continue;
vis[nus]=1;
double di=ttt.dis;
for(int i=head[nus];i;i=tr[i].nxe)
{
int to=tr[i].to;
if(dis[to]-(dis[nus]+tr[i].dis)>0.000001)
{
dis[to]=dis[nus]+tr[i].dis;
q.push((node){dis[to],to});
}
}
}
printf("%.2lf",dis[ed]);
return 0;
}通过以上,也可以看出dj和SPFA的相似之处与一些差别。






















 1012
1012











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








