神经网络中的非线性激活函数：从原理到实践

StarPrayers.

于 2025-10-12 14:30:32 发布

阅读量777

点赞数 8

CC 4.0 BY-SA版权

分类专栏：深度学习文章标签：神经网络人工智能深度学习 pytorch 机器学习算法 python

本文链接：https://blog.csdn.net/Prayer41/article/details/153117508

深度学习专栏收录该内容

8 篇文章

订阅专栏

在神经网络的学习过程中，激活函数是一个看似简单却至关重要的组件。初次接触时，我曾疑惑：为什么不能直接用线性函数呢？为什么需要这些奇怪的曲线？经过深入学习，我才明白激活函数是神经网络能够学习复杂模式的核心所在。这篇博客将记录我对非线性激活函数的理解，方便日后回顾。

一、为什么需要激活函数？

想象一个没有激活函数的神经网络 —— 无论它有多少层，本质上都只是在做线性变换。这是因为线性函数的组合仍然是线性函数。

例如：

如果

第一层计算 y1=w1x+b1；

第二层计算 y2=w2y1+b2；

那么组合起来就是 y2=w2(w1x+b1)+b2=(w2w1)x+(w2b1+b2)，仍然是线性的。

但现实世界中的问题几乎都是非线性的：

房价与面积的关系不是简单的正比
图像中物体的边缘不是直线
语言中的语义关系更是错综复杂

激活函数的核心作用就是为神经网络注入非线性能力，让它能够学习这些复杂的非线性关系。

二、激活函数的本质：神经元的 "开关" 机制

从生物学角度看，激活函数模拟了生物神经元的工作方式 —— 当输入信号超过某个阈值时，神经元被激活并传递信号。

在数学上，激活函数对神经元的输入值（加权和）进行非线性转换：

其中 z=w⋅x+b 是输入的加权和，f() 是激活函数，a 是输出。

这个转换过程可以理解为：

决定哪些信息需要传递（激活）
哪些信息需要抑制（不激活）
以及传递 / 抑制的强度如何

三、常见激活函数解析

1. Sigmoid 函数

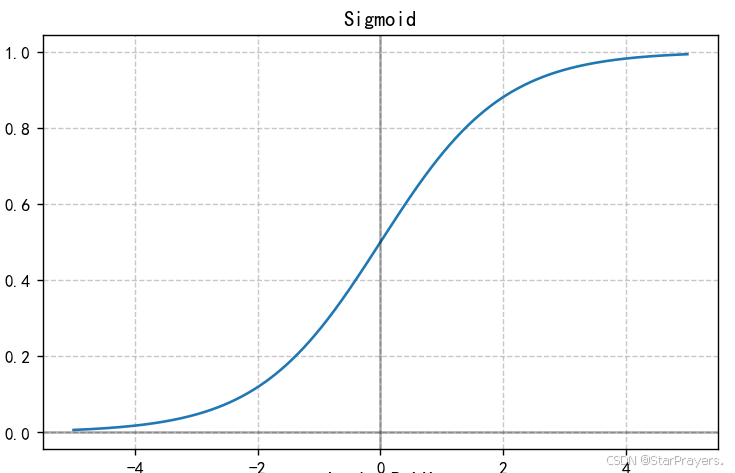
特性：

输出范围严格在 (0, 1) 之间
可以自然地表示概率值
输入越大，输出越接近 1；输入越小，输出越接近 0

适用场景：

二分类问题的输出层（表示属于某一类的概率）
需要输出值在 0 到 1 之间的场景

缺点：

容易出现梯度消失问题（输入绝对值很大时，导数接近 0）
输出不以 0 为中心，可能影响训练效率
计算成本较高（涉及指数运算）

2. Tanh 函数（双曲正切函数）

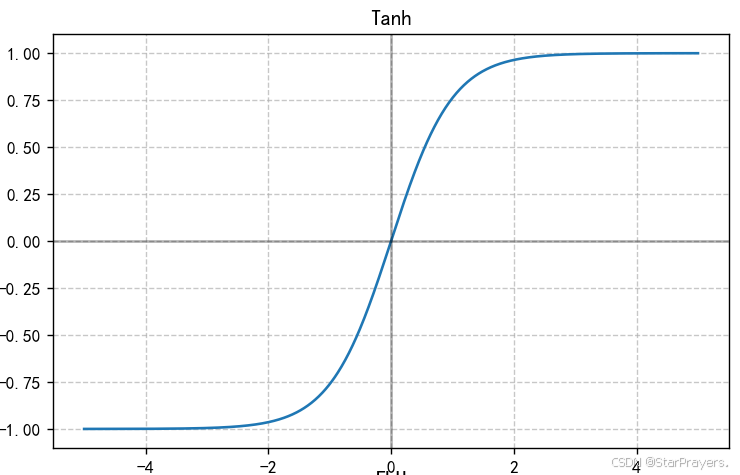
特性：

输出范围在 (-1, 1) 之间
以 0 为中心，比 sigmoid 更对称
形状与 sigmoid 相似，但斜率更陡

适用场景：

隐藏层，尤其是在 RNN 中较为常用
需要输出负值的场景

缺点：

仍然存在梯度消失问题，只是比 sigmoid 稍好
计算成本较高

3. ReLU 函数（修正线性单元）

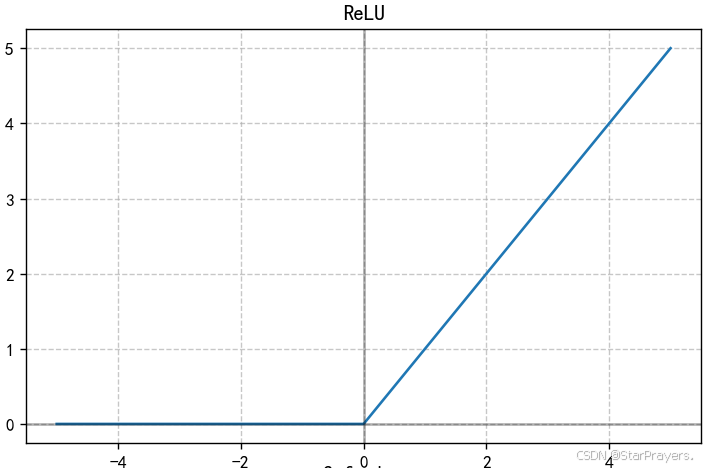
特性：

计算极其简单（只需判断输入是否为正）
当输入为正时，梯度恒为 1，缓解了梯度消失问题
模拟了生物神经元的 "稀疏激活" 特性

适用场景：

大多数神经网络的隐藏层，是目前最常用的激活函数
尤其适合深层卷积神经网络 (CNN)

缺点：

存在 "死亡 ReLU" 问题：当输入长期为负时，神经元可能永久失活
输出不以 0 为中心

4. Leaky ReLU 函数

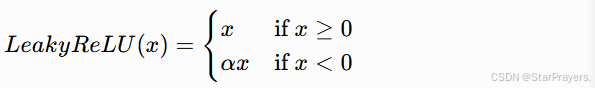
其中 α 是一个小的常数（通常取 0.01）

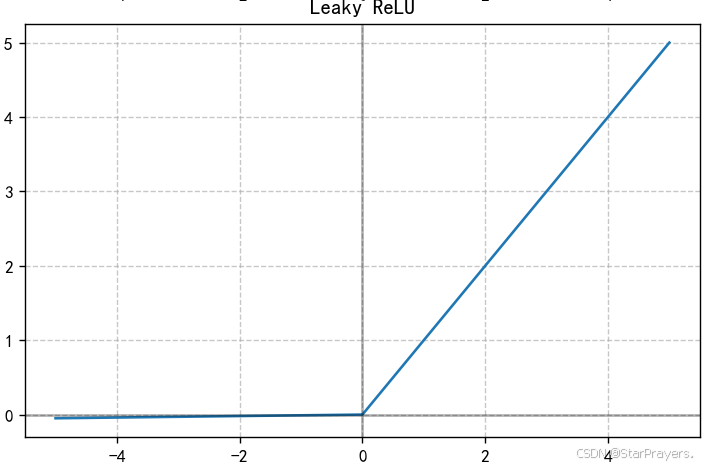
特性：

对 ReLU 的改进，为负输入提供一个小的斜率
解决了 "死亡 ReLU" 问题
保留了 ReLU 计算高效的优点

适用场景：

可以替代 ReLU 作为隐藏层激活函数
尤其适合可能出现较多负输入的场景

缺点：

需要额外调整α参数

5. ELU 函数（指数线性单元）

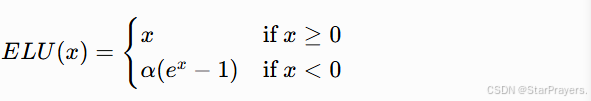
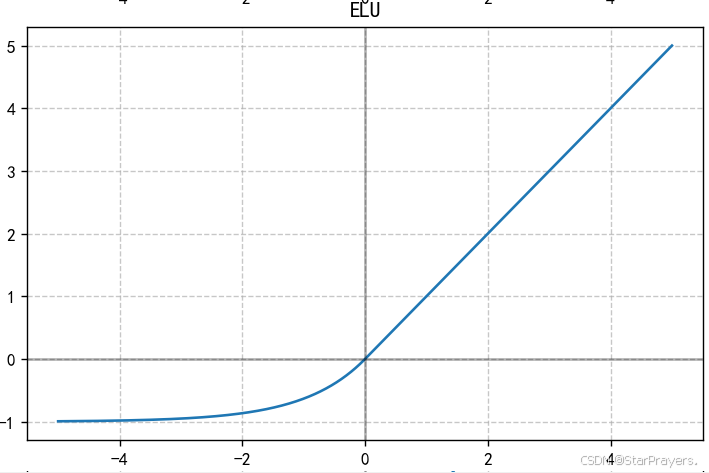
特性：

结合了 ReLU 和 Leaky ReLU 的优点
负输入区域采用平滑的指数曲线，更符合生物神经元特性
均值接近 0，有助于加速收敛

适用场景：

各种神经网络的隐藏层
需要更高训练稳定性的场景

缺点：

计算成本略高于 ReLU 和 Leaky ReLU
需要调整α参数

6. Softplus 函数

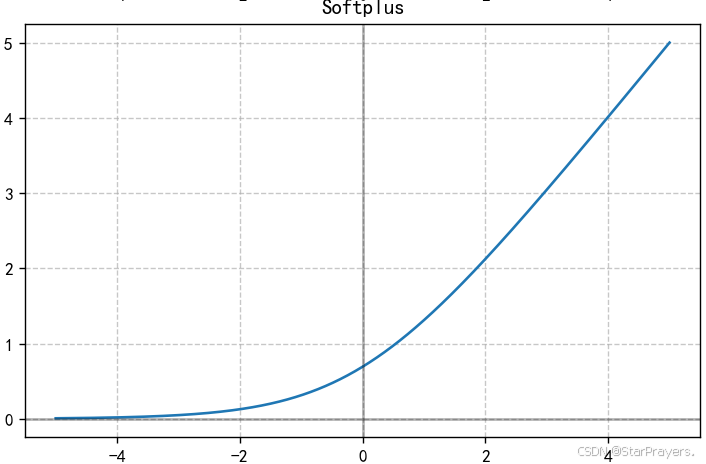
特性：

ReLU 的平滑近似，处处可导
当 x 很大时接近 x，当 x 很小时接近 0
导数是 sigmoid 函数

适用场景：

需要平滑激活函数的场景
替代 ReLU 以避免其不可导点

缺点：

计算成本高于 ReLU
可能存在轻微的梯度消失问题

四、激活函数的选择策略

经过实践总结，我发现以下选择策略比较有效：

隐藏层：
- 优先使用 ReLU（计算快，效果好）
- 如果出现 "死亡 ReLU" 问题，尝试 Leaky ReLU 或 ELU
- 循环神经网络 (RNN) 中可考虑使用 tanh
输出层：
- 二分类问题：使用 sigmoid（输出单个概率值）
- 多分类问题：使用 Softmax（输出多个类别概率分布）
- 回归问题：
  - 输出可以为任意值：不使用激活函数（线性输出）
  - 输出非负值：使用 ReLU
  - 输出在特定范围：使用 sigmoid 或缩放的 tanh
特殊情况：
- 计算资源受限：优先选择 ReLU
- 需要高精度：可尝试 ELU 或其他更复杂的激活函数
- 不稳定的训练：考虑使用 ELU 或带批归一化的 ReLU

五、实践代码：激活函数可视化

可视化代码，用于展示了它们的形状和特性：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider
import matplotlib.font_manager as fm


# 检测系统中可用的中文字体
def get_available_chinese_fonts():
    """获取系统中可用的中文字体列表"""
    chinese_fonts = []
    for font in fm.findSystemFonts():
        try:
            font_name = fm.FontProperties(fname=font).get_name()
            # 常见中文字体关键字
            if any(keyword in font.lower() for keyword in ['sim', 'hei', 'song', 'microsoft yahei', 'deng', 'kai']):
                chinese_fonts.append(font_name)
        except:
            continue
    # 去重并返回
    return list(set(chinese_fonts))


# 获取可用中文字体
available_fonts = get_available_chinese_fonts()
print("系统中可用的中文字体：", available_fonts)

# 设置中文显示，优先使用系统可用字体
if available_fonts:
    # 尝试常用字体
    preferred_fonts = ["SimHei", "Microsoft YaHei", "SimSun", "DengXian", "KaiTi"]
    # 筛选系统中实际存在的字体
    usable_fonts = [font for font in preferred_fonts if font in available_fonts]
    # 如果没有偏好字体，则使用找到的第一个字体
    if not usable_fonts:
        usable_fonts = [available_fonts[0]]
    plt.rcParams["font.family"] = usable_fonts
else:
    # 如果没有找到中文字体，使用默认字体并提示
    print("警告：未找到中文字体，可能无法正常显示中文")
    plt.rcParams["font.family"] = ["Arial Unicode MS", "sans-serif"]

plt.rcParams["axes.unicode_minus"] = False  # 正确显示负号


# 定义常见的激活函数
def sigmoid(x):
    """Sigmoid激活函数"""
    return 1 / (1 + np.exp(-x))


def tanh(x):
    """双曲正切激活函数"""
    return np.tanh(x)


def relu(x):
    """ReLU激活函数"""
    return np.maximum(0, x)


def leaky_relu(x, alpha=0.01):
    """带泄漏的ReLU激活函数"""
    return np.where(x >= 0, x, alpha * x)


def elu(x, alpha=1.0):
    """指数线性单元激活函数"""
    return np.where(x >= 0, x, alpha * (np.exp(x) - 1))


def softplus(x):
    """Softplus激活函数"""
    return np.log(1 + np.exp(x))


# 创建数据
x = np.linspace(-5, 5, 1000)

# 创建图形
fig, axs = plt.subplots(2, 3, figsize=(18, 12))
fig.suptitle('常见的神经网络非线性激活函数', fontsize=20)

# 绘制各个激活函数
axs[0, 0].plot(x, sigmoid(x))
axs[0, 0].set_title('Sigmoid')
axs[0, 0].grid(True, linestyle='--', alpha=0.7)
axs[0, 0].axhline(y=0, color='k', linestyle='-', alpha=0.3)
axs[0, 0].axvline(x=0, color='k', linestyle='-', alpha=0.3)

axs[0, 1].plot(x, tanh(x))
axs[0, 1].set_title('Tanh')
axs[0, 1].grid(True, linestyle='--', alpha=0.7)
axs[0, 1].axhline(y=0, color='k', linestyle='-', alpha=0.3)
axs[0, 1].axvline(x=0, color='k', linestyle='-', alpha=0.3)

axs[0, 2].plot(x, relu(x))
axs[0, 2].set_title('ReLU')
axs[0, 2].grid(True, linestyle='--', alpha=0.7)
axs[0, 2].axhline(y=0, color='k', linestyle='-', alpha=0.3)
axs[0, 2].axvline(x=0, color='k', linestyle='-', alpha=0.3)

axs[1, 0].plot(x, leaky_relu(x))
axs[1, 0].set_title('Leaky ReLU')
axs[1, 0].grid(True, linestyle='--', alpha=0.7)
axs[1, 0].axhline(y=0, color='k', linestyle='-', alpha=0.3)
axs[1, 0].axvline(x=0, color='k', linestyle='-', alpha=0.3)

axs[1, 1].plot(x, elu(x))
axs[1, 1].set_title('ELU')
axs[1, 1].grid(True, linestyle='--', alpha=0.7)
axs[1, 1].axhline(y=0, color='k', linestyle='-', alpha=0.3)
axs[1, 1].axvline(x=0, color='k', linestyle='-', alpha=0.3)

axs[1, 2].plot(x, softplus(x))
axs[1, 2].set_title('Softplus')
axs[1, 2].grid(True, linestyle='--', alpha=0.7)
axs[1, 2].axhline(y=0, color='k', linestyle='-', alpha=0.3)
axs[1, 2].axvline(x=0, color='k', linestyle='-', alpha=0.3)

plt.tight_layout(rect=[0, 0, 1, 0.96])  # 为suptitle留出空间
plt.show()

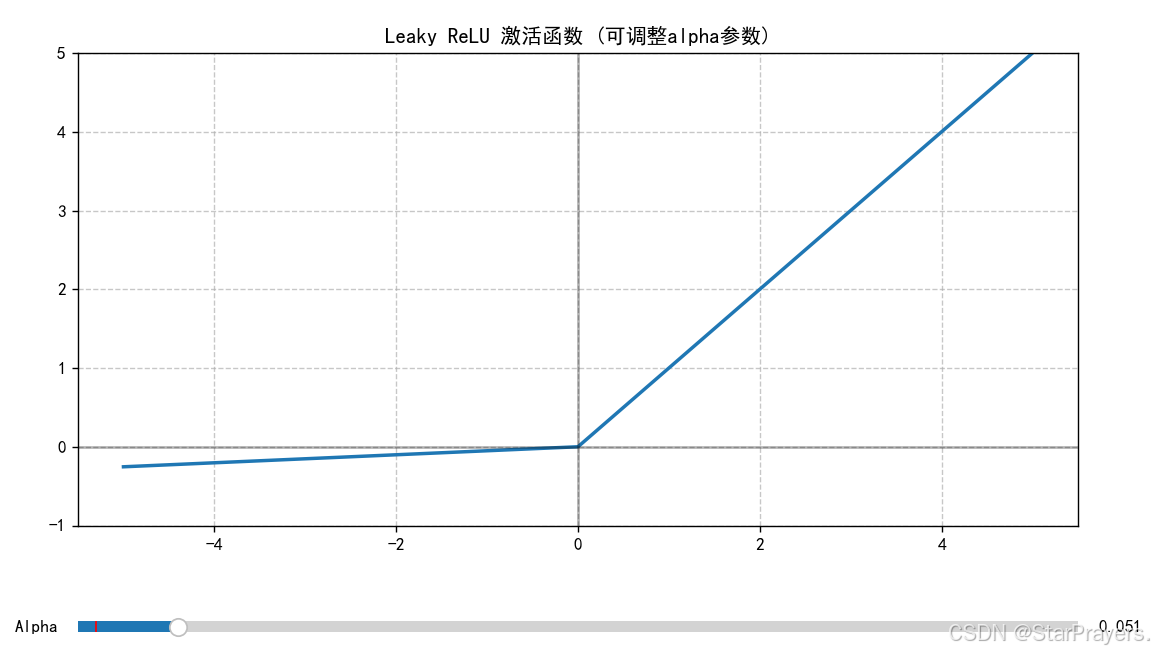
# 创建交互式Leaky ReLU参数调整图
fig, ax = plt.subplots(figsize=(10, 6))
plt.subplots_adjust(left=0.1, bottom=0.25)

alpha_initial = 0.01
line, = ax.plot(x, leaky_relu(x, alpha_initial), lw=2)
ax.set_title('Leaky ReLU 激活函数 (可调整alpha参数)')
ax.grid(True, linestyle='--', alpha=0.7)
ax.axhline(y=0, color='k', linestyle='-', alpha=0.3)
ax.axvline(x=0, color='k', linestyle='-', alpha=0.3)
ax.set_ylim(-1, 5)

# 添加滑块
ax_alpha = plt.axes([0.1, 0.1, 0.8, 0.03])
slider_alpha = Slider(ax_alpha, 'Alpha', 0.001, 0.5, valinit=alpha_initial)


# 更新函数
def update(val):
    alpha = slider_alpha.val
    line.set_ydata(leaky_relu(x, alpha))
    fig.canvas.draw_idle()


slider_alpha.on_changed(update)

plt.show()

运行这段代码，可以直观地看到各种激活函数的形状，并且可以交互式调整 Leaky ReLU 的 alpha 参数，观察其对函数形状的影响。