神经网络求解偏微分方程：基本原理

Python_金钱豹

于 2025-04-01 19:11:25 发布

阅读量1k

点赞数 10

文章标签：神经网络人工智能深度学习自然语言处理语言模型 hive hadoop

本文链接：https://blog.csdn.net/Python_cocola/article/details/146920517

版权

在现代科学与工程计算中，偏微分方程（Partial Differential Equations, PDEs）扮演着至关重要的角色。它们描述了从流体力学到量子力学、从热传导到金融建模等多个领域的现象。然而，解析求解PDEs往往困难重重，尤其是在高维空间或复杂边界条件下。因此，数值方法成为求解PDEs的主要手段。近年来，随着深度学习技术的发展，一种新的数值方法——基于神经网络的解法，开始引起广泛关注。本文将探讨为何以及如何利用神经网络解决偏微分方程的问题。

逼近理论基础

要理解神经网络为什么能够解偏微分方程，首先需要了解基函数逼近的概念。Weierstrass逼近定理指出，在闭区间上连续的任意函数，都可以通过多项式逼近至任意精度。换句话说，对于任何给定的，存在一个多项式，使得在整个区间上：

这个概念告诉我们，可以通过选择适当的“基函数”来近似复杂的连续函数。在传统的数值分析中，我们常使用多项式作为基函数来逼近PDE的解。这种思想不仅适用于多项式，也适用于其他形式的基函数族。例如，切比雪夫多项式、傅里叶级数、样条基函数等都被广泛应用于PDEs的数值求解中。这些方法的核心在于选择一组合适的基函数来逼近目标函数。

在这里插入图片描述

神经网络作为通用逼近器

那么，为什么我们会考虑使用神经网络呢？随着研究的深入，人们发现神经网络同样具备这种逼近能力。通用逼近定理（Universal Approximation Theorem）告诉我们，前馈神经网络同样具有逼近任意连续函数的能力。具体来说，对于任意连续函数，存在一个神经网络 满足：

这表明，神经网络可以被视为一种非常灵活的基函数族，适合用来逼近各种复杂的函数关系。相比传统的多项式或正交基函数，神经网络的优势在于它能够自动学习数据中的非线性特征，无需预先指定具体的函数形式。这意味着，我们可以用神经网络作为一种特殊的基函数族来逼近PDE的解。

在这里插入图片描述

历久弥新的加权余量法

在数值解PDE时，加权余量法是一种常用的技术。其基本思想是选择一组基函数，然后使残差在某种意义下为最小。最常见的几种方法包括配点法、子域法和伽辽金法等。

例如，在配点法中，我们在若干选定点上强制残差为零：

这里，代表PDE的微分算子，是已知的源项。

而当我们使用神经网络作为基函数时，上述过程变为：

类似地，在子域法和伽辽金法中，我们也可以分别使用神经网络来替代传统的多项式或其他基函数。这些方法的核心在于通过调整基函数参数，使得残差尽可能小，从而获得PDE的一个近似解。

物理信息神经网络 (PINNs)

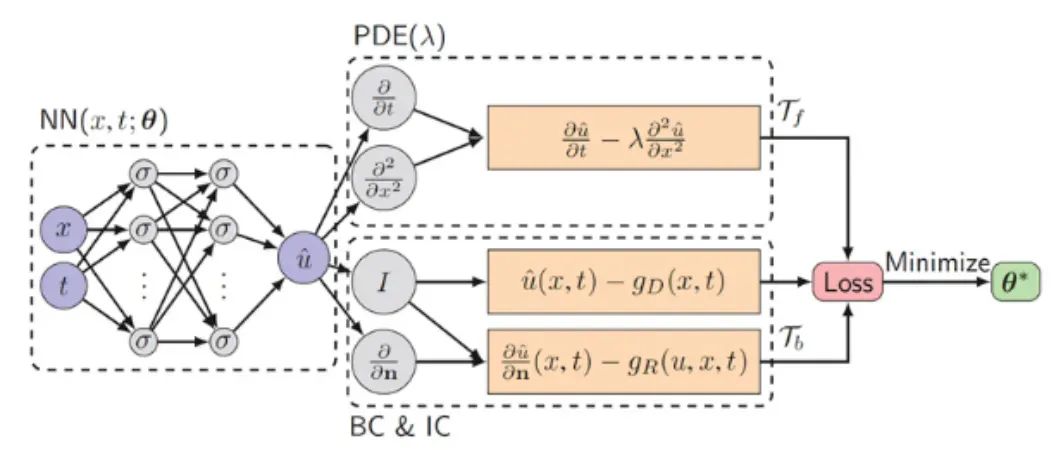
物理信息神经网络（Physics-Informed Neural Networks，简称PINNs）是将神经网络应用于PDE求解的一种现代方法。PINNs的基本思想非常直观：假设解函数是一个神经网络，然后构造一个损失函数，度量它“多大程度上满足微分方程和边界条件”。

具体而言，给定一个PDE：

以及相应的边界条件：

其中，表示问题的定义域，表示其边界。

我们可以构建一个损失函数：

微分方程残差边界条件残差

损失函数由两部分组成：一部分衡量微分方程残差，另一部分衡量边界条件残差。

然后使用梯度下降等优化算法来最小化该损失函数。我们的目标是找到一组参数，使得损失函数尽可能小。这相当于要求神经网络输出的函数同时满足PDE及其边界条件。

PINNs vs 传统方法

与传统的数值方法相比，PINNs有几个显著的优势：

PINNs不受维数灾难的影响。传统方法如有限元法在处理高维PDE时，往往会遇到维度爆炸的问题，导致计算成本急剧增加。而神经网络具有强大的表达能力，能够在高维空间中有效地逼近复杂函数。
PINNs不需要显式的网格划分，这使得它特别适合处理复杂几何形状和不规则边界条件的问题。
PINNs还提供了一种端到端的学习框架。在训练过程中，我们直接优化损失函数，无需手动推导和求解代数方程组。这对于一些难以解析求解的非线性PDE尤其有帮助。

当然，这种方法也面临一些挑战，实际应用中仍有几点需要注意：

由于神经网络的高度非线性和高维特性，优化过程中可能会遇到局部最优解的问题。
为了获得准确的结果，通常需要大量的训练样本覆盖整个解空间。
虽然PINNs不受维数灾难的影响，但对于某些特定类型的PDEs，可能还需要引入额外的技术手段以提高效率和稳定性。

结语

综上所述，神经网络解偏微分方程的本质，并不是什么神秘莫测的方法，而是利用神经网络的强大逼近能力，将PDE求解转化为一个优化问题。无论是传统的多项式、傅里叶级数，还是现代的神经网络，本质上都是在寻找一类可参数化的函数族去逼近PDE的解函数。不同之处在于所选的基函数空间以及满足PDE的方式。通过适当设计损失函数和优化算法，PINNs不仅能够有效地解决各种类型的PDE，而且在高维空间和复杂边界条件下展现出独特的优势。未来，随着算法的不断改进和技术的进步，我们有理由相信，基于神经网络的PDE求解方法将在更多的领域发挥重要作用。

如何学习大模型 AI ？

由于新岗位的生产效率，要优于被取代岗位的生产效率，所以实际上整个社会的生产效率是提升的。

但是具体到个人，只能说是：

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

在这里插入图片描述