神经网络在求解偏微分方程（PDE）方面的应用

通常神经网络是将数据在有限维空间之间进行映射或转换，而用于求解偏微分方程的神经网络则是在无穷大空间之间进行映射。特定的偏微分方程如Stokes方程可对流体流动进行建模，其使用的增量越小，模型精度越高，但数值求解所需时间越长。神经网络擅长拟合像这样的黑盒未知函数，输入和输出均为向量。

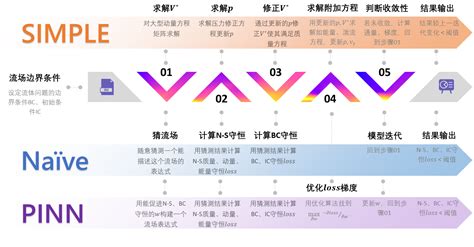
神经网络在求解偏微分方程（PDE）方面的应用已经成为近年来的研究热点。传统的数值方法如有限差分法、有限元法等在处理高维、非线性或复杂边界条件的偏微分方程时，往往面临计算量大、收敛速度慢等问题。而神经网络则以其强大的函数逼近能力和并行计算能力，在这一领域展现出显著的优势。

神经网络通过将偏微分方程转化为优化问题，利用其强大的函数逼近能力来逼近未知函数及其导数，从而实现对PDE的求解。例如，通过设计合适的损失函数衡量预测值与真实解之间的误差，并使用反向传播算法调整参数，神经网络可以逼近PDE的解。这种方法被称为神经PDE或深度学习求解PDE，其核心思想是利用神经网络作为函数逼近工具，通过优化算法调整权重和阈值以最小化预测值与真实解之间的误差。

物理信息神经网络（Physics-Informed Neural Networks, PINNs）是近年来发展起来的一种重要方法。PINNs通过将PDE的残差形式和边界条件作为损失函数的一部分，使得神经网络在训练过程中能够直接学习到PDE的物理规律。这种方法避免了传统数值方法中的离散化过程，从而减少了计算复杂度。PINNs已被证明在处理高维问题时具有显著优势，例如在流体动力学和热传导等领域中表现出色。

<