很多机器学习的算法也常用于NLP的任务。见《机器学习算法原理与编程实践》
目前最流行的算法思想包含以下两大流派:基于概率论和图论的概率图模型;基于人工神经网络的深度学习的理论
4.1 概率论
4.1.2、朴素贝叶斯分类的流程可以表示如下:
第一阶段,训练数据生成训练样本集:TF-IDF
第二阶段,对每个类别计算P(yi)。
第三阶段,对每个特征属性计算所有划分的条件概率
第四阶段,对每个类别计算p(x | yi) p(yi)
第五阶段,以p(x | yi) p(yi)的最大项作为x的所属类别。
4.1.3 文本分类
1、One-Hot表达
2、权重策略:TF-IDF方法,倾向于过滤掉常见的词语,保留重要的词语
文本分类的实现:
Nbayes_lib.py
# -*- coding: utf-8 -*-
import sys
import os
from numpy import *
import numpy as np
def loadDataSet():
postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him', 'my'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0, 1, 0, 1, 0, 1] # 1 is abusive, 0 not
return postingList, classVec
class NBayes(object):
def __init__(self):
self.vocabulary = [] # 词典
self.idf = 0 # 词典的idf权重向量
self.tf = 0 # 训练集的权重矩阵
self.tdm = 0 # P(x|yi)
self.Pcates = {} # P(yi) 是一个类别词典
self.labels = [] # 对应每个文本的分类,是一个外部导入的列表
self.doclength = 0 # 训练集文本数
self.vocablen = 0 # 词典词长
self.testset = 0 # 测试集
# 导入和训练数据集,生成算法必需的参数和数据结构
def train_set(self, trainset, classVec):
self.cate_prob(classVec) # 计算每个分类在数据集中的概率:P(yi)
self.doclength = len(trainset)
# 生成词典
tempset = set()
[tempset.add(word) for doc in trainset for word in doc ]
self.vocabulary = list(tempset)
self.vocablen = len(self.vocabulary)
# 计算词频数据集
self.calc_wordfreq(trainset)
# 按分类累计向量空间的每维值:P(yi)
self.build_tdm()
# 计算在数据集中每个分类的概率: P(yi)
def cate_prob(self, classVec):
self.labels = classVec #
labeltemps = set(self.labels) # 获取全部分类
for labeltemp in labeltemps:
# 统计列表中重复的分类: self.labels.count(labeltemp)
self.Pcates[labeltemp] = float(self.labels.count(labeltemp)) / float(len(self.labels))
# 生成普通的词频向量
def calc_wordfreq(self, trainset):
self.idf = np.zeros([1, self.vocablen]) # 1 * 词典数
self.tf = np.zeros([self.doclength, self.vocablen]) # 训练集文件数 × 词典数
for index in xrange(self.doclength): # 遍历文本
for word in trainset[index]: # 遍历文本中的每个词
self.tf[index, self.vocabulary.index(word)] += 1 # 词数加1
#
for signleword in set(trainset[index]):
self.idf[0, self.vocabulary.index(signleword)] += 1
# 按分类累计向量空间的每维值: P(x | yi)
def build_tdm(self):
self.tdm = np.zeros([len(self.Pcates), self.vocablen]) # 类别行 * 词典列
sumlist = np.zeros([len(self.Pcates), 1]) # 统计每个类别的总值
for index in xrange(self.doclength):
self.tdm[self.labels[index]] += self.tf[index] # 将同一类别的词向量空间值加总
# 统计每个分类的总值 是一个标量
sumlist[self.labels[index]] = np.sum(self.tdm[self.labels[index]])
self.tdm = self.tdm / sumlist # P(x | yi)
# 将测试集映射到当前词典
def map2vocb(self, testdata):
self.testset = np.zeros([1, self.vocablen])
for word in testdata:
self.testset[0, self.vocabulary.index(word)] += 1
# 预测分类结果, 输出预测的分类类别
def predict(self, testset):
if np.shape(testset)[1] != self.vocablen:
print "输入错误: 测试集长度与词典不相等"
exit(0)
predvalue = 0
predclass = ""
for tdm_vect, keyclass in zip(self.tdm, self.Pcates):
# P(x | yi) P(yi)
temp = np.sum(testset * tdm_vect * self.Pcates[keyclass])
# 变量tdm,计算最大分类值
if temp > predvalue:
predvalue = temp
predclass = keyclass
return predclass
# 生成tf-idf
def calc_tdidf(self, trainset):
self.idf = np.zeros([1, self.vocablen]) # 1 * 词典数
self.tf = np.zeros([self.doclength, self.vocablen]) # 训练集文件数 × 词典数
for index in xrange(self.doclength): # 遍历文本
for word in trainset[index]: # 遍历文本中的每个词
self.tf[index, self.vocabulary.index(word)] += 1 # 词数加1
# 消除不同句长导致的偏差
self.tf[index] = self.tf[index] / float(len(trainset[index]))
for signleword in set(trainset[index]):
self.idf[0, self.vocabulary.index(signleword)] += 1
self.idf = np.log(float(self.doclength) / self.idf)
self.tf = np.multiply(self.tf, self.idf) # 矩阵与向量的点乘 tf X idf# -*- coding: utf-8 -*-
from Nbayes_lib import *
dataSet, listClasses = loadDataSet()
nb = NBayes()
nb.train_set(dataSet, listClasses)
#nb.map2vocb(dataSet[1])
nb.map2vocb(['my', 'dog', 'is', 'stupid'])
print nb.predict(nb.testset) # 输出分类结果4.2 信息熵
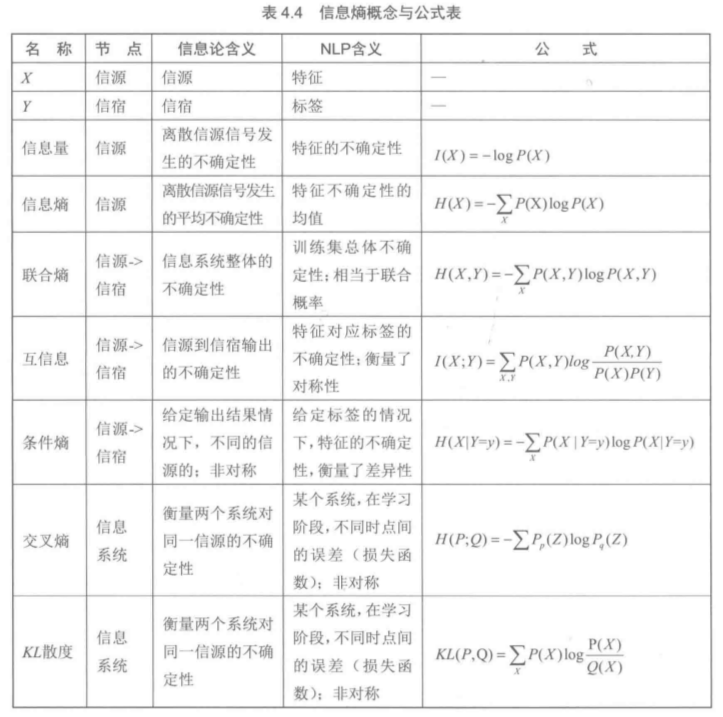
如果说概率是对事件确定性的度量,那么信息(包括信息量和信息熵)就是对事件不确定性的度量。1948年香农借用热力学中热熵的概念(热熵是表示分子状态混乱程度的物理量),解决了对信息的量化度量问题,也常用来对不确定性进行度量。
信息量与信息熵:
- 信息熵的本质是信息量的期望
- 信息熵是对随机变量不确定性的度量。随机变量X的熵越大,说明它的不确定性也越大。若随机变量退化为定值,则熵为0
- 平均分布是“最不确定”的分布
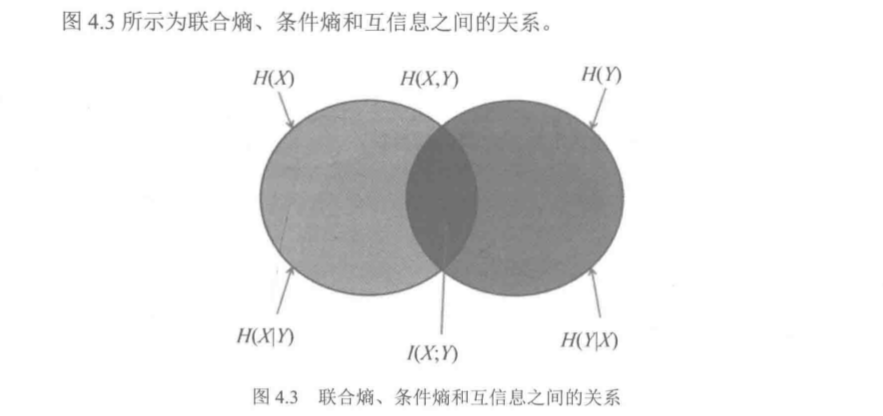
互信息、联合熵、条件熵:
互信息定义:I(y,x) = I(y) - I(y | x) = log( P(y|x) / P(y) )
互信息的性质如下:
1)互信息可以理解为,收信者收到信息X后,对信源Y的不确定性的消除
2)互信息=I(先验事件)-I(后验事件=log ( 后验概率 / 先验概率 )
3)互信息是对称的
平均互信息又称为信息增益
I(X;Y) = Sum( P(X,Y) log ( P(X,Y) / P(X) P(Y) )
联合熵:借助联合概率分布对熵的自然推广,
条件熵:利用条件概率分布对熵的一个延伸
交叉熵和KL散度:
交叉熵常用来衡量两个概率分布的差异性,在Logistic中的交叉熵为其代价函数
信息熵在NLP的意义:
对于任何语言系统的抽象模型都是一个信息系统,引入信息熵的本质意义在于从信息论的角度来考察一个语言系统,并且对其行为(编码和解码)提供了统一的测度。
4.3 NLP与概率图模型
概率图模型的动机来源于建立一套领域无关的通用自动(智能)推理理论,从中揭示智能推理的内在机制。
我们解决非确定性问题的传统思路就是利用概率论的思想,但是随着问题的复杂不断增加,传统的概率方法显得越来越力不从心。图模型的引入使人们可以将复杂问题得到适当的分解:其中,变量表示为节点,变量与变量之间的关系表示为边,这样就使问题的以结构化。然后,根据图的结构进行训练和计算推理得出最终的结果。因此,概率图理论就自然地分为三个部分,分别为:概率图模型表示理论、概率图模型推理理论和概率图模型学习理论。
1)模型的表示:分两类:贝叶斯网络(有向无环图)和马尔科夫随机场(无向图)。NLP中最常用的就是各种基于马尔科夫性的各种概率图模型。
2)模型的学习:不同模型因为原理不同,能够处理的语言问题也不同,比如朴素贝叶斯模型在处理文本分类方面精度很高;最大熵模型在处理中文词性标注问题上表现很好,条件随机场模型处理中文分词、语义组块等方面的精度很高;Semi-CRF在处理命名实体识别精度很高。
3)模型的预测:最大的后验概率为预测的结果。
如果隐马尔科夫模型是朴素贝叶斯模型的序列化模型扩展,则条件随机场可以理解为最大熵模型的序列扩展
统计语言模型:n-gram
极大似然设计:
4.4 隐马尔科夫模型简介
马尔科夫链:指时间和状态都是离散的马尔科夫过程,T+1次结果只受第T次结果的影响,即只与当前状态有关,而与过去状态,即与系统的初始状态和此次转移前的所有状态无关。
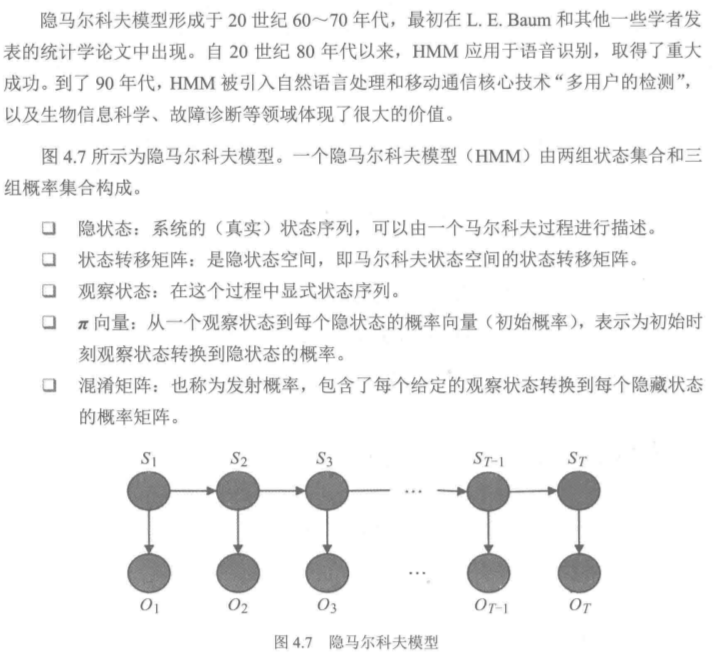
一个实例:
hmm.py
# -*- coding: utf-8 -*-
from numpy import *
startP = mat([0.63, 0.17, 0.20]) # 起始概率
# 状态转移概率
stateP = mat([ [0.5, 0.25, 0.25],
[0.375, 0.125, 0.375],
[0.125, 0.675, 0.375] ])
# 发射(混合)概率
emitP = mat([ [0.6, 0.20, 0.05],
[0.25, 0.25, 0.25],
[0.05, 0.10, 0.50] ])
# 计算概率: 干旱---干燥---潮湿
stateEmit = multiply(startP, emitP[:,0].T)
print stateEmit
print "argmax:", stateEmit.argmax()
# 计算干燥的概率:
state2Emit = stateP * stateEmit.T
state2Emit = multiply(state2Emit, emitP[:,1])
print state2Emit.T
print "argmax:", state2Emit.argmax()
# 计算潮湿的概率:
state3Emit = stateP * state2Emit
state3Emit = multiply(state3Emit, emitP[:,2])
print state3Emit.T
print "argmax:", state3Emit.argmax()显然,随着矩阵的规模增大,算法的计算量是灾难性的。
Viterbi算法的实现:
可以发现HMM的计算结果呈现出如下的规律性。
- 最优路径是有网络中概率最大的节点构成的一条路径
- 初始状态矩阵和t0时刻的转移概率决定了第一天天气状态的所有概率。但是,对后续各天气状态产生决定影响的只有最大概率的那个天气状态。argmax()
- 之后的每一天都如此,t+1时刻的概率同时受到t时刻转移概率和当天的显状态影响。但是只有最大概率的那个天气状态才对后续状态产生决定性的影响。argmax()
# -*- coding: utf-8 -*-
from numpy import *
def viterbi(obs, states, start_p, trans_p, emit_p):
'''
obs: 观测序列
states: 隐状态
start_p: 初始概率
trans_p: 转移概率
emit_p: 发射概率
'''
V = [{}] # 路径概率表V[时间][隐状态] = 概率
for y in states:
V[0][y] = start_p[y] * emit_p[y][obs[0]]
for t in xrange(1, len(obs)):
V.append({})
for y in states:
# 概率 隐状态 = 前状态是y0的概率 × y0转移到y的概率 * y表现为当前状态的概率
V[t][y] = max([ (V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]] ) for y0 in states ])
result = []
for vector in V:
temp = {}
temp[ vector.keys()[ argmax( vector.values() ) ] ] = max(vector.values())
result.append(temp)
return result
states = ('Sunny', 'Cloudy', 'Rainy')
obs = ('dry', 'dryish', 'soggy')
start_p = {'Sunny':0.63, 'Cloudy':0.17, 'Rainy':0.20 }
trans_p = {
'Sunny' : {'Sunny':0.5, 'Cloudy': 0.375, 'Rainy':0.125},
'Cloudy' : {'Sunny':0.25, 'Cloudy': 0.125, 'Rainy':0.625},
'Rainy' : {'Sunny':0.25, 'Cloudy': 0.375, 'Rainy':0.375},
}
emit_p = {
'Sunny' : {'dry':0.60, 'dryish': 0.20, 'soggy':0.05},
'Cloudy' : {'dry':0.25, 'dryish': 0.25, 'soggy':0.25},
'Rainy' : {'dry':0.05, 'dryish': 0.10, 'soggy':0.50},
}
print viterbi(obs, states, start_p, trans_p, emit_p)4.5 最大熵模型
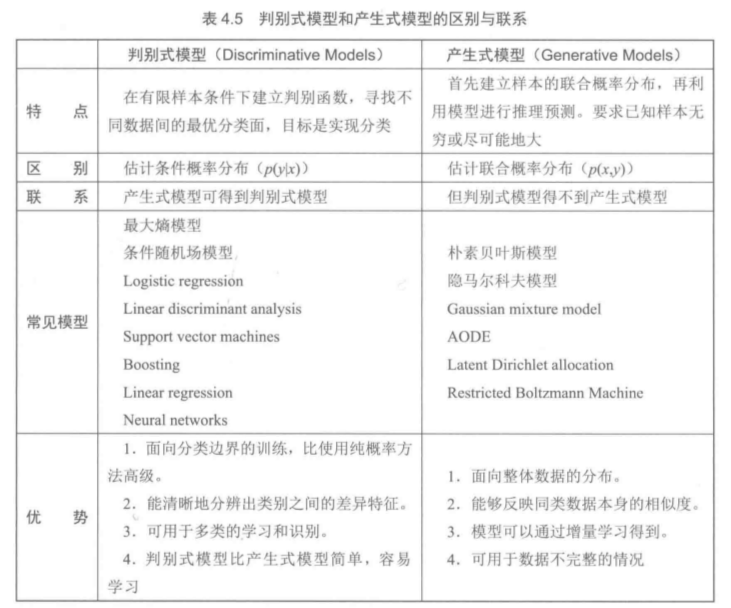
隐马尔科夫模型将标注问题看作一个马尔科夫链,针对相邻标注的关系进行建模,其中每个标记都对应一个概率。HMM在概率图模型中属于产生式模型,需要依赖一个联合概率分布。为了得到这个联合概率分布,产生式模型需要枚举出所有可能的观察序列,这在NLP的实际运算过程中往往是很困难的。
另一方面,NLP的大量真实语料中,观测序列更多地是以一种多重的交互特征形式表现,观测序列之间广泛存在长程相关性。例如,在命名实体识别任务中,由于专名结构所具有的复杂性,利用简单的特征函数往往无法涵盖所有的特性(它无法使用多于一个标记的特征)。
此时,需要引入一个新的模型。由于该模型获得的是所有满足约束条件的模型中信息熵极大的标签,因此称为最大熵模型,如下特点:
- 可以使用任意的复杂相关特征。
- 可以灵活地设置约束条件,通过约束条件的多少来调节模型对未知数据的适应度和对已知数据的拟合程度。
- 它还能自然地解决统计模型中参数平滑的问题。
从词性标注谈起:
特征和约束:
一个实例:
data.txt
Outdoor Sunny Happy
Outdoor Sunny Happy Dry
Outdoor Sunny Happy Humid
Outdoor Sunny Sad Dry
Outdoor Sunny Sad Humid
Outdoor Cloudy Happy Humid
Outdoor Cloudy Happy Humid
Outdoor Cloudy Sad Humid
Outdoor Cloudy Sad Humid
Indoor Rainy Happy Humid
Indoor Rainy Happy Dry
Indoor Rainy Sad Dry
Indoor Rainy Sad Humid
Indoor Cloudy Sad Humid
Indoor Cloudy Sad Humid# -*- coding: utf-8 -*-
import sys
import os
from collections import defaultdict
import math
class MaxEnt(object):
def __init__(self):
self.feats = defaultdict(int)
self.trainset = []
self.labels = set() # 标签集
def load_data(self, file):
for line in open(file):
fields = line.strip().split()
if len(fields) < 2: continue # 特征数要大于两列
label = fields[0] # 默认第一列是标签
self.labels.add(label)
for f in set(fields[1:]):
self.feats[(label, f)] += 1
# (label,f) 元组是特征
print label, f
self.trainset.append(fields)
# 初始化参数
def _initparams(self):
self.size = len(self.trainset)
# GIS 训练算法的M参数
self.M = max( [len(record) - 1 for record in self.trainset] )
self.ep_ = [0.0] * len(self.feats)
for i,f in enumerate(self.feats):
# 计算经验分布的特征期望
self.ep_[i] = float(self.feats[f]) / float(self.size)
self.feats[f] = i # 为每个特征函数分配id
self.w = [0.0] * len(self.feats) # 初始化权重
self.lastw = self.w
# 特征函数
def Ep(self):
ep = [0.0] * len(self.feats)
for record in self.trainset:
features = record[1:]
prob = self.calprob(features) # 计算条件概率p(y|x)
for f in features:
for w,l in prob:
if (l,f) in self.feats:
idx = self.feats[(l,f)]
# sum(1/N * f(y,x) * p(y|x)), p(x) = 1/N
ep[idx] += w * (1.0/self.size)
return ep
# 收敛---终止条件
def _convergence(self, lastw, w):
for w1, w2 in zip(lastw, w):
if abs(w1 - w2) >= 0.01:
return False
return True
# 训练
def train(self, max_iter=1000):
self._initparams() # 初始化参数
for i in range(max_iter):
#print 'iter %d ...' % (i+1)
self.ep = self.Ep() # 计算模型分布的特征期望
self.lastw = self.w[:]
for i,win in enumerate(self.w):
delta = 1.0/self.M * math.log(self.ep_[i] / self.ep[i] )
self.w[i] += delta # 更新 w
#print self.w, self.feats
# 判断算法是否收敛
if self._convergence(self.lastw, self.w):
break;
# 计算每个特征权重的指数
def probwgt(self, features, label):
wgt = 0.0
for f in features:
if (label, f) in self.feats:
wgt += self.w[ self.feats[(label, f)] ]
return math.exp(wgt)
# 计算条件概率
def calprob(self, features):
wgts = [ (self.probwgt(features, l), l) for l in self.labels ]
Z = sum( [ w for w,l in wgts ] ) # 归一化参数
prob = [ (w/Z, l) for w, l in wgts ] # 概率向量
return prob
# 预测函数
def predict(self, input):
features = input.strip().split()
prob = self.calprob(features)
prob.sort(reverse=True)
return prob
model = MaxEnt()
model.load_data('data.txt') # 导入训练集
model.train()
print model.predict("Rainy Happy Dry")4.6 条件随机场模型
CRF最早有Lafferty等人于2001年提出,其模型思想的主要来源是隐马尔科夫模型。
对HMM模型的三个基本问题的解决用到了HMM模型中提到的方法如Forward-Backward算法和Viterbi算法。可以把CRF看成一个无向图模型或马尔科夫随机场,它是一种用来标记和切分序列化数据的统计模型。该模型是在给定需要标记的观察序列的条件下,计算整个标记序列的联合概率,而不是在给定当前状态的条件下,定义下一个状态的分布。标记序列的分布条件属性,可以让CRF很好地拟合现实数据,而在这些数据中,标记序列的条件概率信赖于观察序列中非独立的、相互作用的特征,并通过赋予特征以不同权重来表示特征的重要程度。

























 8519
8519

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








