载波相位调制（PSK/DPSK)

---

前言

本节介绍了载波相位调制，也就是PSK和DPSK的调制和解调过程，以及讲述了仿真的具体步骤。其中许多内容是与前面的幅度调制类似的，程序也是根据上一篇改过来的，只不过这篇去掉了码转换，上篇用的是格雷码。

---

一、调制和解调的过程

上图是调制和相干解调的过程，右侧的符号也是程序中所用的符号。过程也说明了相干解调的正交方法。

二、仿真的过程

1.程序1-验证解调情况

代码如下（可以改变信噪比ESNO的值，来人为观察误码率，在测试的时候可以把信噪比提高）：

%% PSK//DPSK
clear all;close all;clc;
n_symbol=1e4;                           %%符号个数
T=2;                                  %%表达式中的参数
fs=100;
ts=1/fs;
t=0:ts:T-ts;
fc=5;                                 %%载波频率
c=sqrt(2/T)*exp(j*2*pi*fc*t);         %%载波信号生成两个正交载波
c1=sqrt(2/T)*cos(2*pi*fc*t); 
c2=-sqrt(2/T)*sin(2*pi*fc*t);
M=8;
%%可以使用格雷码，后面也需要用格雷码解出
ESNO=120   ;                          %%单位dBD   
snr=10.^(ESNO/10);                    %%转换成单位线性值
msg=randi(M,1,n_symbol);
msgmod=dpskmod(msg-1,M).';            %%dpsk调制
% msgmod=pskmod(msg-1,M).';             %%psk调制
x=real(msgmod*c);
x1=reshape(x.',1,length(msgmod)*length(c));
s_pow=norm(x1).^2/(n_symbol);                  %%这里是符号的平均功率，而不是每一个采样点
sigma=sqrt(s_pow/(2*snr));                     %%根据线性值的信噪比和信号功率求出噪声功率
x_n=x1+sigma*randn(1,length(x1));              %%加性噪声后的信号
x_n1=reshape(x_n,length(c),length(msgmod));    %%将合成信号分解一下以便后面的相干计算
r1=(c1*x_n1).*T/length(c);                     %%相干计算
r2=(c2*x_n1).*T/length(c);
r=r1+j*r2;
y1=dpskdemod(r,M)+1;                           %%dpsk解调 
% y1=pskdemod(r,M)+1;                            %%psk解调 

%想要将原符号来做比较验证误码率，可以为了将数字信号展开做比较
for i=1:n_symbol                    
    msg_x((100*i-99):100*i)=msg(i);
    y1_x((100*i-99):100*i)=y1(i);  
end
figure;
subplot(411);
plot(msg_x);title(['原信号,信噪比为',num2str(ESNO),'dB']);
subplot(412);
plot(x1);title('原信号+载波');
subplot(413);
plot(x_n);title('原信号+载波+噪声');
subplot(414);
plot(y1_x);title('解调信号');

下面第一张图片是DPSK下的原信号、原信号+载波（调制信号）、原信号+载波+噪声（调制信号经过信道）、解调信号。为了方便观察，将符号数设为5，信噪比设的也很大。

第一张图片是PSK下的原信号、原信号+载波（调制信号）、原信号+载波+噪声（调制信号经过信道）、解调信号。

2.程序2-不同信噪比下的误码率

判断不同信噪比的误码率，是建立在上端程序的基础上，创建16组不同信噪比的对比组，最终得出不同信噪比情况下的误码情况。其中理论误比特率公式如下所示，其中Q函数在上一篇也说过就是与erfc很类似，只不过系数稍微变一下。

%% PSK//DPSK
clear all;close all;clc;
n_symbol=1e5;                       %%符号个数
T=2;                                %%表达式中的参数
fs=100;
ts=1/fs;
t=0:ts:T-ts;
fc=10;
c=sqrt(2/T)*cos(2*pi*fc*t);         %%载波信号
c1=sqrt(2/T)*cos(2*pi*fc*t); 
c2=-sqrt(2/T)*sin(2*pi*fc*t);
M=4;
ESNO=0:15;                          %%单位dBD   创建16组不同信噪比的情况做自变量
snr=10.^(ESNO/10);                  %%转换成单位线性值
msg=randi(M,1,n_symbol);
% msgmod=dpskmod(msg-1,M).';            %%dpsk调制
msgmod=pskmod(msg-1,M).';             %%psk调制
x=msgmod*c;
x1=reshape(x.',1,length(msgmod)*length(c));
s_pow=norm(x1).^2/(n_symbol);
for i=1:length(ESNO)
    sigma=sqrt(s_pow/(2*snr(i)));
    x_n=x1+sigma*randn(1,length(x1));
    x_n1=reshape(x_n,length(c),length(msgmod));
    r1=(c1*x_n1).*T/length(c);                     %%相干计算
    r2=(c2*x_n1).*T/length(c);
    r=r1+j*r2;
%     y1=dpskdemod(r,M)+1;                           %%dpsk解调 
    y1=pskdemod(r,M)+1;                            %%psk解调 
    [err,ber(i)]=biterr(msg-1,y1-1,log2(M));    
    [err,ser(i)]=symerr(msg,y1);
end
ser_real=2*qfunc(sqrt(2*snr)*sin(pi/M));
semilogy(ESNO,ser,'-bo',ESNO,ber,'-k*',ESNO,ser_real,'-ro'); 
xlabel('信噪比（dB）');legend('误比特率','误符号率','理论的误比特率');

下面第一张图则表示在DPSK下，不同信噪比下的误比特率、误符号率以及理论误比特率的情况。

第二张图则表示在PSK下，不同信噪比下的误比特率、误符号率以及理论误比特率的情况。

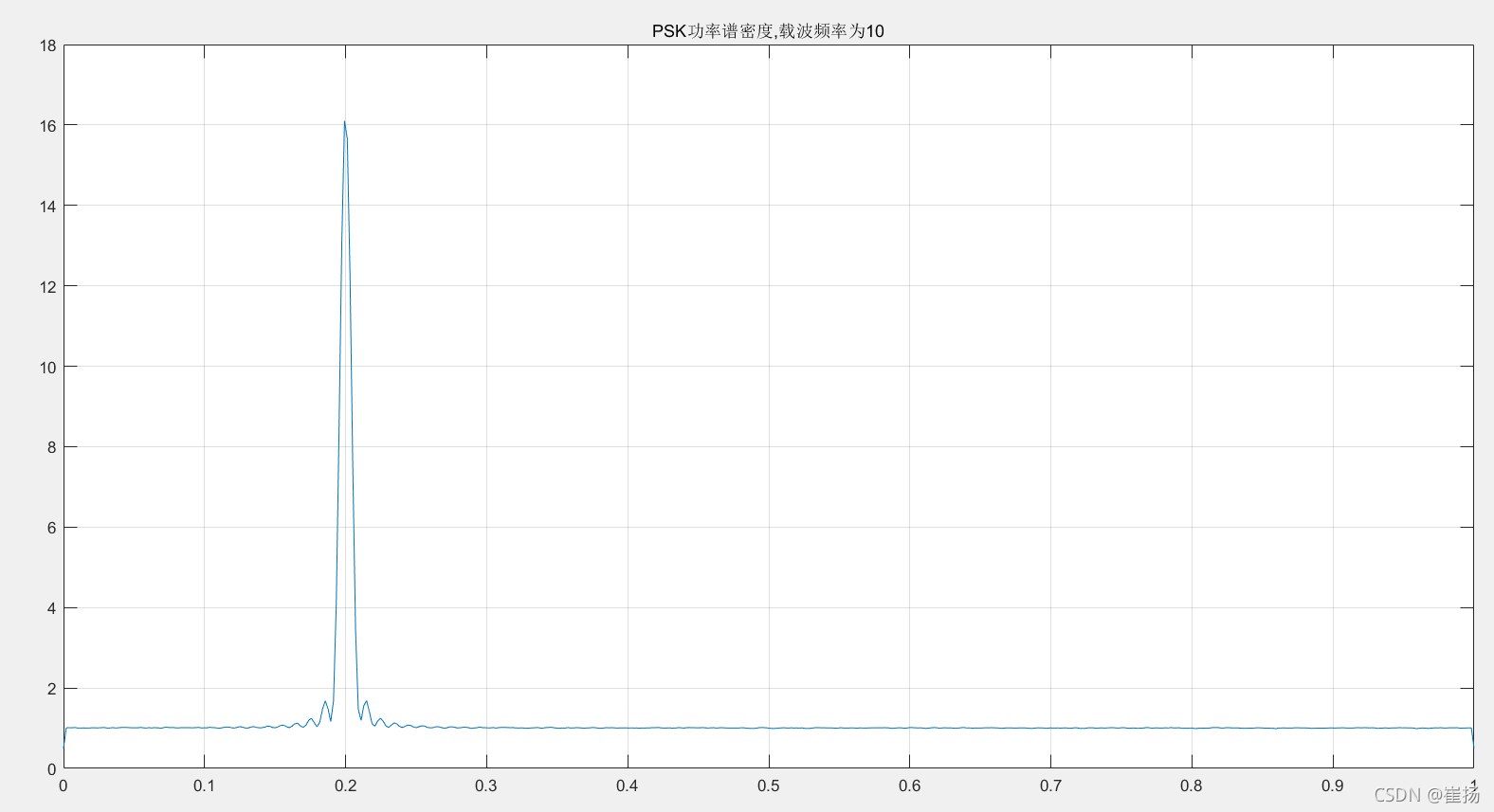
3.调制信号的功率谱密度

根据求功率谱密度估计的方法（此链接几乎涵盖了大部分普遍使用的经典功率谱密度）。（需要使N小于x_n）上节忘记说明为什么要求一下功率谱密度了：
由于在非合作的通信信号检测中，在确定有信号的情况下，需要得知载波频偏和符号速率等参数才可以进行下一步解调。可以通过功率谱密度函数得出归一化频率峰值点在0.2Π上
通过公式求得载波频偏

N=1024;Nfft=1024;
window=hamming(N); noverlap=N/2;
[Pxx,f]=pwelch(x_n,window,noverlap,Nfft);
figure;
plot(f/pi,Pxx);grid on;title(['PSK功率谱密度,载波频率为',num2str(fc)]);

总结

本节介绍了数字信号载波传输中的载波相位调制，也就是将所要传输的信息放在载波的相位中传输。这里的相干计算解调的步骤在上篇文章ASK\PAM已经提到，所以省略。