千古割圆术

二分割圆

为圆周率，被定义为

其中， 为圆周，而 为半径。为简化计算，令 。下面，我们尝试通过正多边形逼近来获得π 。我们从6等分圆开始。

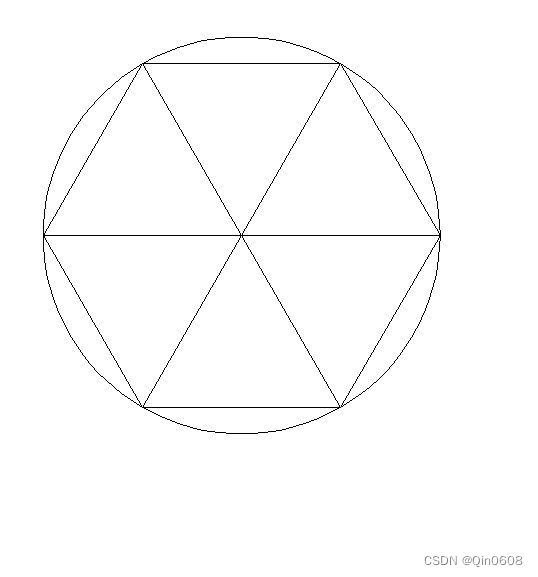
上图展示了6等分情形，此时的正6边形边长 为 ，那么，

显然，这样 的精度很低，但是可以想象，通过不断对圆进行二分，能将圆周继续割成12等分，24等分，48等分……继续分割k 次后，圆周就被割成 等分，圆就被切割为 个小扇形。当k 趋于无穷，该正n 边形周长 就无限接近于圆周。于是，

对正 边形再次二分，得到的正 边形的边长 与正 边形的边长 存在下面的递推关系：

这样，就可以从 开始，不断得到 ， ……

同时，考虑到古代人没有计算器，你无法直接用计算器中的开方按钮得到开方。因此，这里要求你必须通过开方公式计算上述迭代中的开方 。用自己写的开方函数名为sqrt_myself( )以避免和自带的sqrt( )函数冲突，此外，建议你设置一个很小的误差使得开方迭代停止，如 = 10-6。

在这一步中，你最后需要计算得到两个参数：正96边形的 值 ，以及正192边形的 值 。

松弛加速

下面是割圆术最为精彩的部分，进行松弛加速。刘徽设计，

来得到π3072 ，其中ω  = 。请利用你在第2步中得到的π96 和π192 根据超松弛加速获得π3072 。

补充

开方公式

对任意给定初值x0>0 均有下面的开方公式收敛于 ：

, k =0, 1, 2……

需要给出一个很小的误差使得迭代停止。

代码

function result = sqrt_myself(a)
    x = 1;
    for i = 1:1e12
        x2 = 0.5 * (x + a / x);
        if abs(x2 - x) < 1e-6
            result = x2;
            return;
        end
        x = x2;
    end
end
% 计算π值
function pi_diedai = diedai_pi(n)
    k=log2(n/6)+1;
    sides = 6;
    r = 1;
    l_n = r;
    for i = 1:k
        l_n = sqrt_myself((l_n / 2)^2 + (r - sqrt_myself(r^2 - (l_n / 2)^2))^2);
        sides = sides * 2;
        pi_diedai = sides * l_n / (2 * r);
    end
    fprintf('迭代_%d次\n',k);
    fprintf('I_%d: %f\n',n,l_n);
    fprintf('π_%d: %.10f\n',n,pi_diedai);
end
%递推计算
pi_96=diedai_pi(96);
pi_192=diedai_pi(192);
pi_3072=diedai_pi(3072);
%松弛加速
pi_3072_relax = (1 + 36/105) * pi_192 - 36/105 * pi_96
fprintf('利用递推计算得到的π_3072: %.10f\n', pi_3072);
fprintf('利用超松弛加速得到的π_3072: %.10f\n', pi_3072_relax);
pi_big=diedai_pi(6*(2^20));
fprintf( 'π_big: %.10f\n',pi_big);