半导体物理 第五章 半导体载流子的平衡态统计分布

状态密度

状（能）态密度的定义

状态密度：单位能量间隔内的状态数目。能量变化导致k状态变化，然后导致k空间体积的变化（即等能面的扩张或收缩），进而导致状态数的变化。

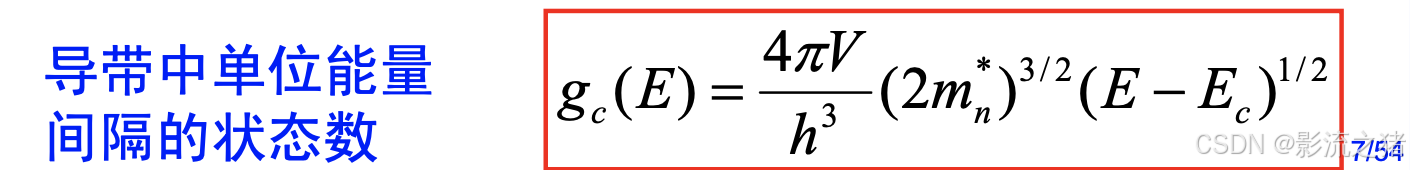
特点：

• 状态密度与能量呈抛物线关系。
• 有效质量越大，状态密度也就越大。
• 仅适用于能带极值附近。

对于实际的半导体来说，硅的导带有六个相同的椭球型等能面，锗有四个（八个半椭球），因此要给状态密度乘相应的倍数，因此定义了电子状态密度有效质量。

而对于空穴，要考虑硅和锗的价带，极值点在k=0，分为轻空穴和重空穴两支能带，总状态密度是轻重两支能带状态密度之和，定义出了空穴状态密度有效质量。

状（能）态密度汇总

费米能级和载流子的统计分布

费米分布函数

费米分布函数是表示能量为E的一个量子态被电子占据的几率，对所有这样的量子态求和，一定会得到总的电子数目。其中费米能级随着温度而发生变化。

当能量和费米能级差值很大，费米分布函数就退化为玻尔兹曼分布（实际上是电子较少的时候忽略泡利不相容原理的结果），就是图中绿色的线。

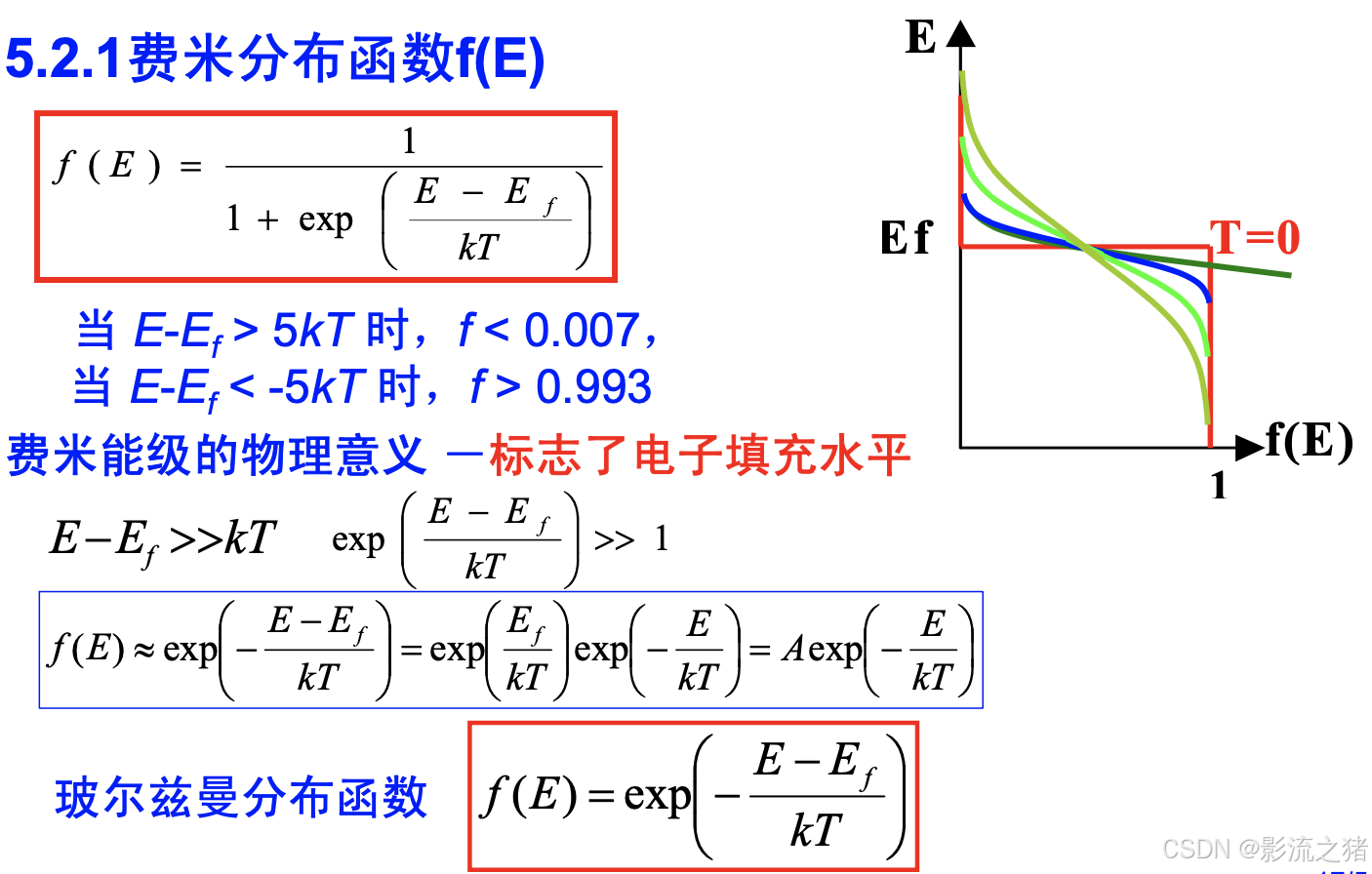
因为一个位置如果没有被电子占据，那么它就被空穴占据，所以空穴的费米分布函数和电子费米分布函数相加等于1。

导带电子和价带空穴浓度

导带电子浓度的求解，就是用电子状态密度（有多少可允许的量子态），乘以费米分布函数（每个量子态的电子数量的期望），对整个导带积分。假设导带底远高于费米能级，那么费米分布函数变为玻尔兹曼分布，由于玻尔兹曼分布以指数形式减少，所以实际上积分中占主要部分的是接近导带底的部分，所以将电子状态密度适用于整个导带，积分上限改为无穷。

数学处理后，得到平衡态的导带电子浓度，引入导带有效状态密度，它和温度有关。

同理，得到价带平衡空穴浓度和价带空穴有效状态密度，它和温度有关。

载流子浓度乘积有重要性质，只和材料参数和温度有关，和费米能级、掺杂浓度无关：

本征半导体中的载流子统计

本征载流子浓度

根据n=p=ni，得出np=ni^2，这是电中性条件，开根得到本征载流子浓度，本征载流子浓度只和温度有关。

本征载流子浓度和温度的对数关系：

禁带越宽，极限工作温度越大。

本征半导体的费米能级位置

利用n=p求出费米能级，基本上在禁带中线处。

杂质半导体中的载流子统计

非补偿情形（单一杂质）

杂质能级的分布函数（这里受主能级的基态简并度是4）：

术语定义：施主能级上的电子浓度就是未电离的施主浓度，电离施主浓度就是用总掺杂浓度减去未电离的施主浓度，也等于向导带激发的电子的浓度。受主能级和空穴浓度同理，空穴电离实际上就是空穴离开受主能级，价带电子占据受主能级。

单一杂质的电中性条件：

对n型半导体中载流子浓度进行讨论，分为几个区域：

低温弱电离区：

中等电离区和强电离区：

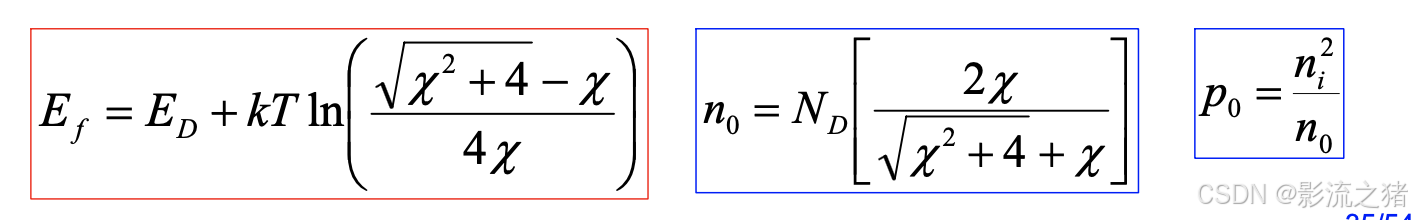
过渡区（强电离区->本征激发）：

本征激发区：

n型半导体的费米能级随温度变化：

n型半导体的电子浓度随温度变化：

强电离不同掺杂水平的费米能级：

补偿情形

电中性条件：

低温弱电离区：由于施主杂质较多，费米能级钉扎在施主能级附近，远在受主能级之上，受主能级完全被电子填充，

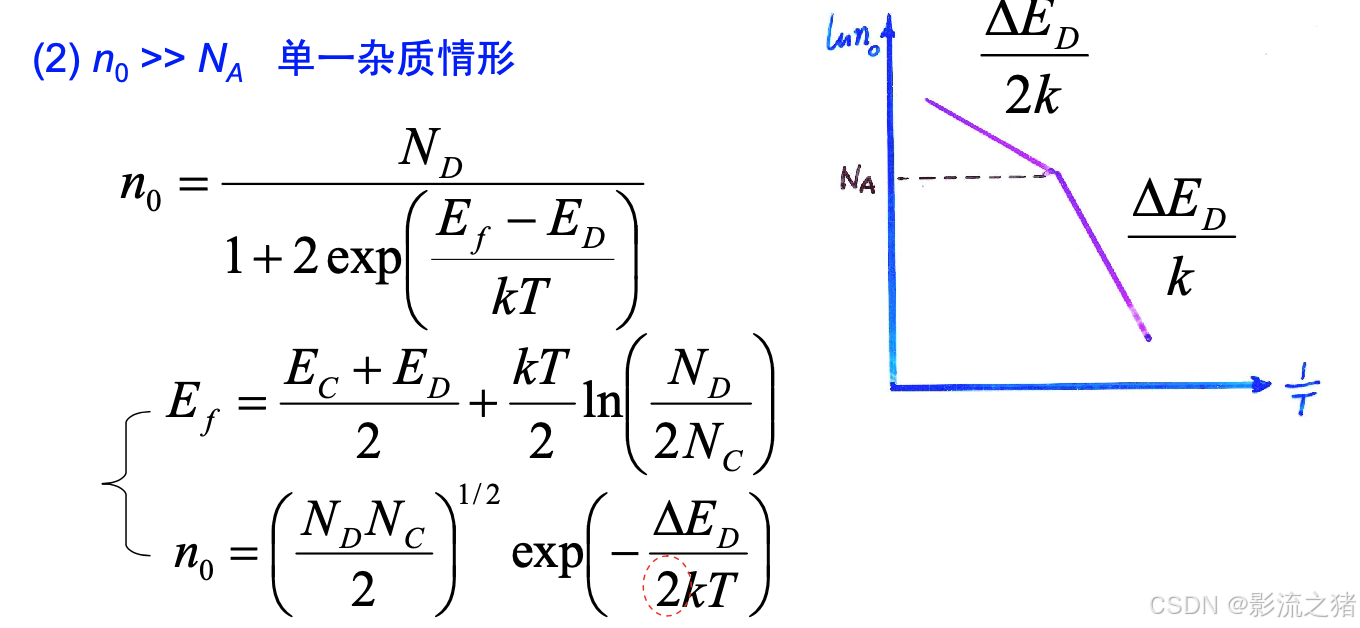
对数坐标图上的斜率有差别，临界点是电子浓度等于受主浓度。

强电离区：

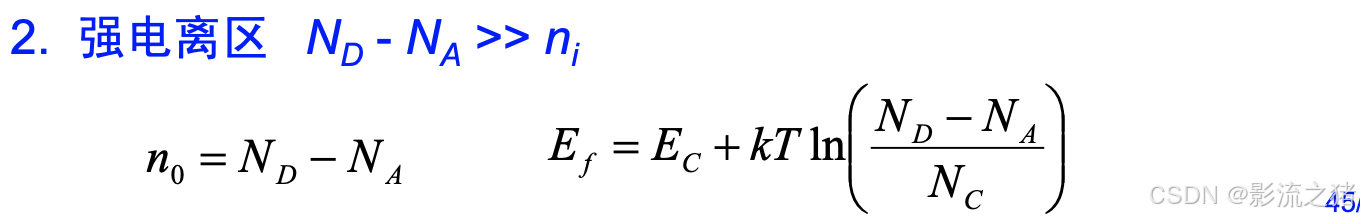
过渡区：

本征激发区：

简并半导体

简并的出现

当掺杂浓度大于导带有效状态密度时，费米能级高于导带底，玻尔兹曼分布不适用，要考虑泡利不相容原理。

简并半导体的载流子浓度

电子浓度和空穴浓度求出：

简并化条件

简并化条件：

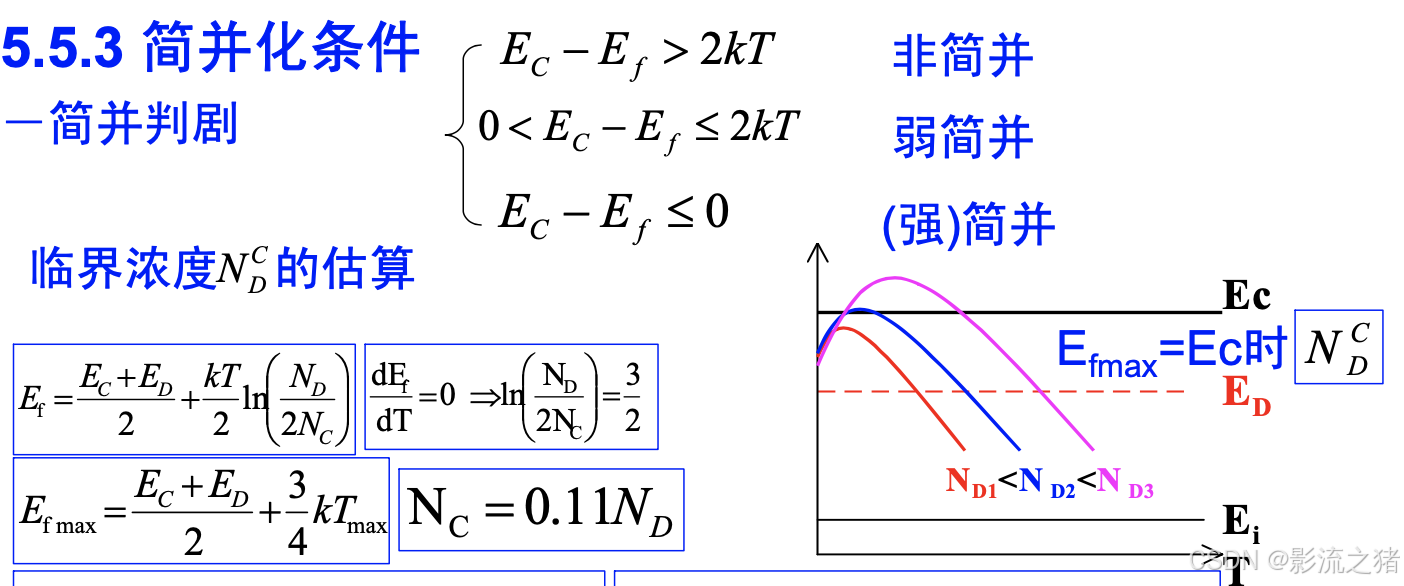
简并掺杂浓度：

简并时杂质的电离

简并时杂质不能充分电离。一般非简并时，费米能级在施主能级之下，施主容易电离；而简并时，费米能级超过导带底，施主不容易电离。