半导体物理 第六章 半导体中载流子的输运

载流子的漂移运动

电导的微观理论

电导的宏观理论是欧姆定律，据此可以推导出微观形式的欧姆定律，其中电导率受到载流子浓度和载流子迁移率的影响。

半导体的电导率和迁移率

据此可以推导出载流子平均漂移速度和载流子迁移率、电场强度的关系，对空穴和电子有不同的迁移率，可以得到空穴电流密度和电子电流密度。

载流子的散射

载流子散射的概念

不满带的电子能够导电，因为电子的速度之和不为零。

散射几率、平均自由时间和迁移率的关系

散射几率：单位时间受到散射的次数。

平均自由时间（弛豫时间）：平均每次散射之间的时长。

平均漂移速度：假设两次散射之间是匀加速运动，求在散射前的速度。

可以求出平均漂移速度和弛豫时间的关系，对于各向异性的半导体来说，就是对不同的导带加权求平均值，可以得到电子电导有效质量。

载流子散射的主要机制

散射的原因：周期势场被破坏（晶体偏离理想），产生了微扰势。

1. 电离杂质中心散射（库仑力的作用、弹性散射）。温度越高，散射几率越小；掺杂浓度越大，散射几率越大。
2. 晶格振动散射（声子散射）。晶格振动类似于谐振子，可以产生格波（晶格振动波）。格波分为光学波和声学波，都是两横一纵，光学波的能量较高。

声子是一种准粒子，既有能量又有动量，声子散射遵循动量和能量守恒。

具有单能谷的半导体，对电子起散射作用的主要是长波，即q=0附近的波，靠近中间的是纵波，两边是横波。$\omega$较小时是弹性散射，较大时是非弹性散射。

可以得出光学波和声学波散射几率。一般情况下（非热载流子，速度不饱和）考虑声学波散射，温度越高，声学波散射几率越大。

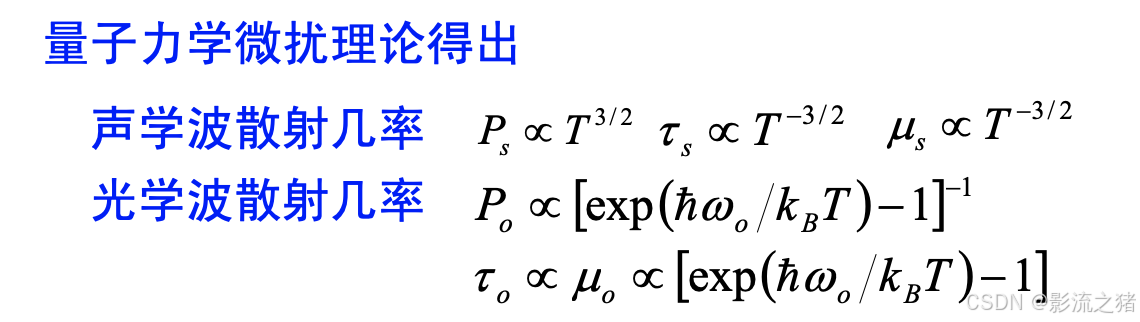
此外，还有一些其他的散射机制：等价能谷间散射（非弹性散射）；中性杂质散射（重掺杂、低温）；缺陷散射。

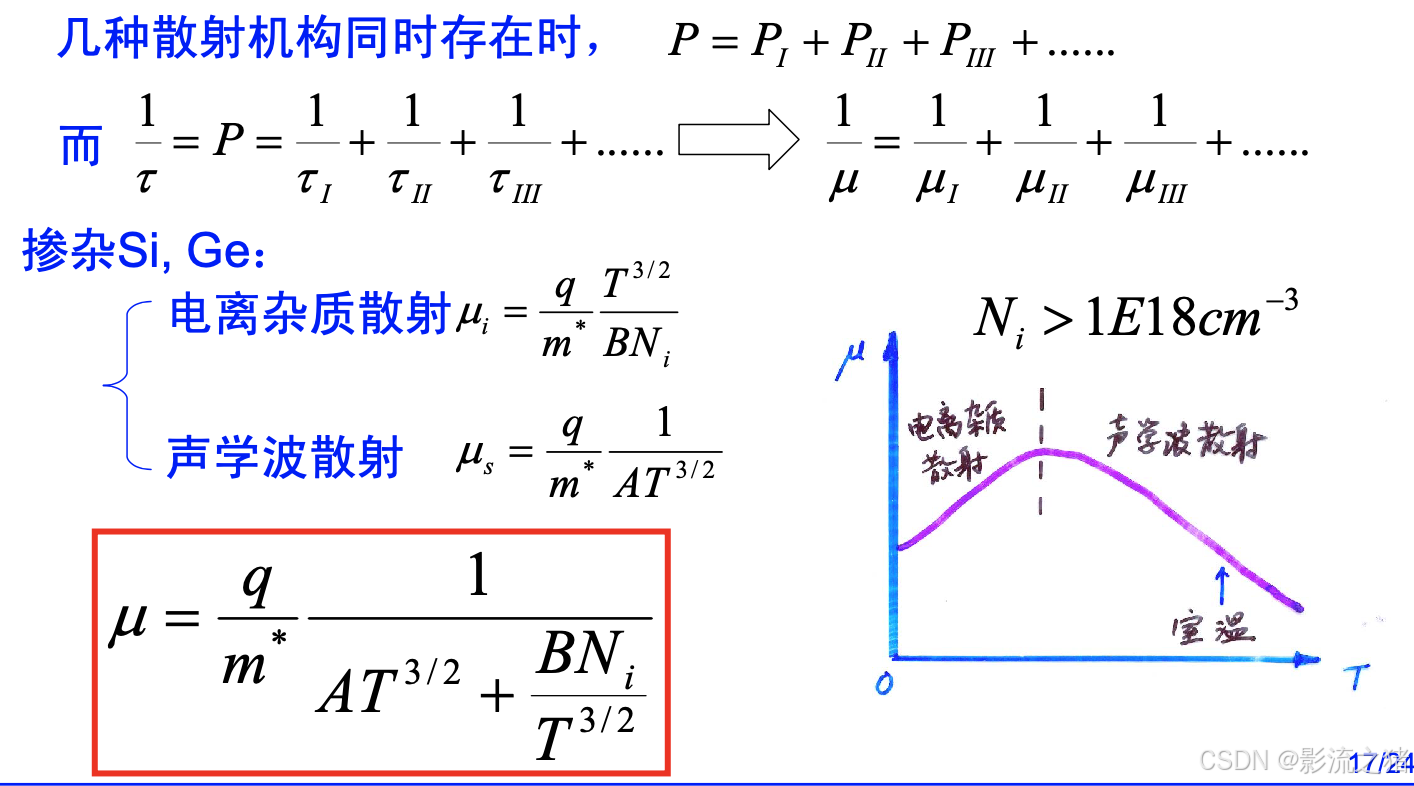
迁移率与杂质浓度和温度的关系

迁移率与杂质浓度和温度的关系

几种散射机构同时存在时，散射几率是线性相加的。据此，主要考虑电离杂质散射和声学波散射，得到迁移率和杂质浓度和温度的关系。式中A项是声学波散射，B项是电离杂质散射。

电阻率与杂质浓度的关系

电阻率随杂质浓度增大单调下降。在轻掺杂情形下，迁移率弱依赖于掺杂浓度，电子浓度与掺杂浓度成正比，因此在对数坐标图上是一条直线；重掺杂情况下，迁移率减小，且不完全电离，电阻率比直线要大。

电阻率与温度的关系

对于本征半导体，主要由本征载流子浓度决定，电阻率单调下降。

对于杂质半导体，载流子可以通过杂质电离和本征激发来获得，迁移率通过电离杂质散射和晶格散射影响。

AB段：温度较小，温度增大时，杂质电离增大，本征激发忽略（载流子数量增大），电离杂质散射减小，晶格振动散射忽略（迁移率增大）。

BC段：温度中等，电离杂质完全电离，本征激发次要（载流子数量不变），电离杂质散射次要，晶格振动散射增大（迁移率减小）。

CD段：温度高，电离杂质电离次要，本征激发增大（载流子数量增大），电离杂质散射次要，晶格振动散射次要（迁移率不变）。

强电场下的输运

欧姆定律的偏移和热载流子

低场下线性、中场下1/2次方、强场下饱和。

弛豫时间和电子速度有关，低场下热运动平均速度远大于漂移速度，主要由热运动平均速度决定；随着漂移速度增加，弛豫时间减少，迁移率下降。

强场下发射光学声子，速度可以饱和。

强场下热载流子的能量很高，可以光学声子散射，也可以发生能谷间散射。