【BZOJ 3224】普通平衡树-Splay

最新推荐文章于 2018-10-13 22:09:10 发布

Ripped

最新推荐文章于 2018-10-13 22:09:10 发布

阅读量410

点赞数

分类专栏： splay 文章标签：平衡树 splay

本文链接：https://blog.csdn.net/Ripped/article/details/55056350

版权

splay 专栏收录该内容

1 篇文章 0 订阅

订阅专栏

之前用SBT做过一次，splay的操作都快忘记了所以拿这道题练练手。
splay支持的操作和SBT一样，只不过多出了一个splay操作，所以写法上会有一些不同，并且splay相比SBT更加能够应付极端数据。

基本操作

定义结构体

这次用了压缩的写法，tme用来存当前节点出现的次数，size用来存当前子树的大小。话说这两个东西是可以互相转化的但是为了后面方便（个屁）所以这么写。

struct TREE
{
    int ftr,son[3],key,tme,size;
} tree[N];

旋转

splay的旋转和SBT的旋转是一样的，只不过这里把左旋和右旋写在了一起。
PS讲道理应该是0表示左孩子1表示右孩子这样就可以位运算啦但是我太菜了所以1表示左孩子2表示右孩子。
然后之前的那个压缩写法之所以这么短是因为下面调用了maintain过程，这里为了理解方便就不这么写了。
这里维护的东西有点多，但是本质上还是一样的，以后找个简单点的模板改一下。

void rotate(int x,int w)//w=1左旋，w=2右旋
{
    int y = tree[x].ftr;
    tree[y].size = tree[y].size - tree[x].size + tree[tree[x].son[w]].size;
    tree[x].size = tree[x].size - tree[tree[x].son[w]].size + tree[y].size;
    tree[y].son[3-w] = tree[x].son[w];
    if (tree[x].son[w] != 0) tree[tree[x].son[w]].ftr = y;
    tree[x].ftr = tree[y].ftr;
    if (tree[y].ftr != 0)
        if (y == tree[tree[y].ftr].son[1]) tree[tree[y].ftr].son[1] = x;
            else tree[tree[y].ftr].son[2] = x;
    tree[y].ftr = x; 
    tree[x].son[w] = y;
}

双旋

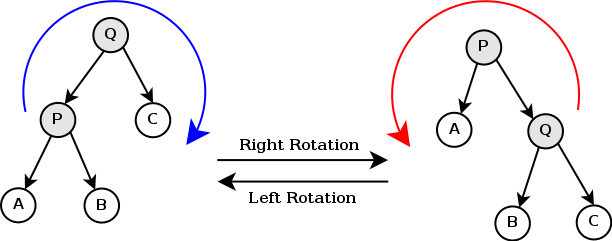
有了旋转（单旋）的基础，我们就可以定义一个splay独有的操作——双旋。在这里，我们将左旋记为Zig，右旋记为Zag。
通过这样不断地旋转，就可以将目标节点转到根节点。

Zig-Zig与Zag-Zag

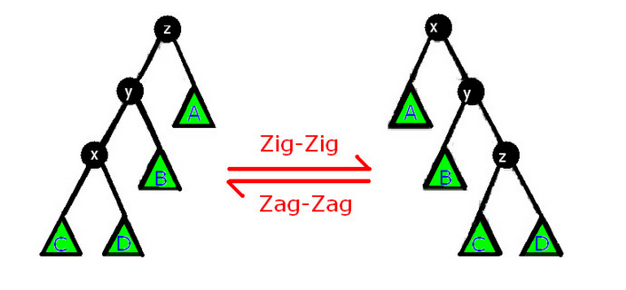
Zig-Zig与Zag-Zag通过两次同方向旋转，适用于目标节点及其父节点都是左孩子（左图）或都是右孩子（右图）。
注意：这里的双旋，是先对父节点旋转再对自己旋转！

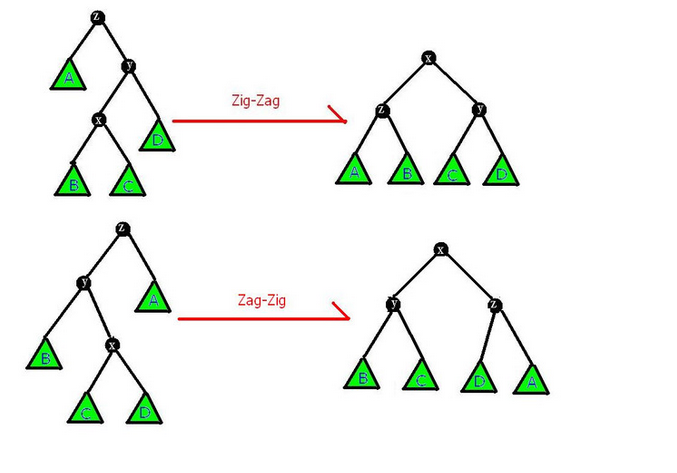
Zig-Zag与Zag-Zig

Zig-Zag与Zag-Zig通过两次不同方向旋转，适用于目标节点及其父节点分别在不同侧。
注意：这里的双旋，都是对自己旋转！

//其中定义：
#define ZIG rotate(x,2);
#define ZAG rotate(x,1);
#define ZIGZIG {rotate(y,2); rotate(x,2);}
#define ZAGZIG {rotate(x,1); rotate(x,2);}
#define ZAGZAG {rotate(y,1); rotate(x,1);}
#define ZIGZAG {rotate(x,2); rotate(x,1);} 
void splay(int x)
{
    while (tree[x].ftr != 0)
        {
            int y = tree[x].ftr;
            if (tree[y].ftr == 0)
                if (x == tree[y].son[1]) ZIG else ZAG
            else 
            if (tree[tree[y].ftr].son[1] == y)
                if (x == tree[y].son[1]) ZIGZIG else ZAGZIG
            else
                if (x == tree[y].son[2]) ZAGZAG else ZIGZAG
        }
    root = x;
}

双旋的复杂度证明

终于等到了这里！双旋复杂度！
之前SBT因为其优秀的严格平衡性质（也就是不断地maintain维护）可以保证其复杂度为logn，但是在splay中并没有maintain这一操作，而旋转操作的目标仅仅是将目标节点转至根节点，那么splay是如何保证其logn的复杂度呢？
在双旋中我们注意到：

Zig-Zig与Zag-Zag是先对父节点旋转再对自己旋转！
Zig-Zag与Zag-Zig都是对自己旋转！

那么问题就出在双旋上。我们想象一下如果只定义单旋会怎么样？每次只要判断是左孩子和右孩子，对应用Zig或Zag就好了，是不是简单很多？
但是手工模拟一下就会发现Zig-Zig操作如果都对自己旋转，结果就是树高不再稳定！
是的的确双旋需要判断的东西有点多，但是这也是为了效率考虑，虽然一般不会来卡splay，但万一呢？

双旋的话tarjan证明了复杂度均摊为O(logn)。单旋的话就是妥妥O(n)了啊，虽然不卡的话很快，但是单旋比较好写。如果不太记得双旋怎么写的话可以写单旋，一般能过，但是要注意千万不要用单旋去写LCT，因为一条链就可以卡掉(눈_눈我就这么狗带的)如果会双旋最好用双旋咯！信Tarjan得永生⊙ω⊙
from：尛焱轟
https://www.zhihu.com/question/40777845/answer/88181917

好的那就双旋吧。。。。

搜索

这里还要定义一个恶心的搜索，然后这就会牵扯到一个非常严肃的问题。。那就是为什么要用搜索！
在SBT中我一直习惯用递归，因为递归写法加上标记回传代码非常简洁。在写splay的时候我也是习惯性地写成了递归，
但是但是但是！重要的事情说三遍！
在每次操作后（所有操作）都要调用一次splay，也就是说把出现频率高的节点向上移动，但是这样就改变了整棵树的形态，这就导致回溯的时候许多信息都是错误的。。。
我卡了好久！
害得我现在的代码又丑又丑又丑。。。

int search(int x,int key)
{
    int r = x;
    while (tree[r].key != key)
        {
            if (key < tree[r].key)
                {
                    if (tree[r].son[1] == 0) break;
                    r = tree[r].son[1];
                }   else
                {
                    if (tree[r].son[2] == 0) break;
                    r = tree[r].son[2];
                }
        }
    return r;
}

插入

对没错就是插入！我就是用递归插入！
先上不用递归的代码（加了初始节点特判我也不知道怎么写在一起干脆就这样了）：

void insert(int x)  
{
    bool flag; int u;
    if (tot == 0)  
    {  
        tot = 1; 
        tree[1].ftr = 0; tree[1].key = x;
        tree[1].size = tree[1].tme = root = 1; 
        return;  
    }  
    int k = search(root,x);  
    if (tree[k].key == x)  
    {  
        tree[k].tme++;
        u = k;  
        flag = true;  
    }  
    else  
    {  
        tot++;  
        tree[tot].key=x;  
        tree[tot].ftr=k;  
        tree[tot].size = tree[tot].tme = 1;  
        if (tree[k].key > x) tree[k].son[1] = tot;
                else tree[k].son[2] = tot;  
        flag = false;  
    }  
    while (k > 0)  
    {  
        tree[k].size++;  
        k = tree[k].ftr;  
    }  
    if (flag) splay(u); else splay(tot);  
}

然后之前的画风是这样的。。没有斜杠的。。

void insert(int &x,int key,int last)
{
    if (x == 0)
        {
            x = ++tot;
            tree[x].son[1] = tree[x].son[2] = 0;
            tree[x].size = tree[x].tme = 1;
            tree[x].key = key; tree[x].ftr = last;
            //splay(x);
        }    else
        {
            tree[x].size++;
            if (key < tree[x].key) insert(tree[x].son[1],key,x);
            if (key > tree[x].key) insert(tree[x].son[2],key,x);
            //if (key == tree[x].key) {tree[x].tme++; splay(x);}
            if (key == tree[x].key) tree[x].tme++;
        }
}

删除

没错删除也不能按照原来的方法删除。。。

void remove(int x,int key)
{
    if(key > tree[x].key) remove(tree[x].son[2],key);  
    else if(key < tree[x].key) remove(tree[x].son[1],key);  
    else
        {
            splay(x);
            if (tree[x].tme > 1) {tree[x].tme--; tree[x].size--;}
                else
                if (tree[x].son[1] == 0)
                    {
                        int y = tree[x].son[2];
                        tree[x].son[2] = tree[x].size = tree[x].key = tree[x].tme = 0;
                        root = y; tree[root].ftr = 0;
                    }   else
                    {
                        tree[tree[x].son[1]].ftr = 0;
                        int y = extreme(tree[x].son[1],MMAX);
                        tree[root].son[2] = tree[x].son[2];
                        tree[root].size = tree[root].size + tree[tree[x].son[2]].size;
                        if (tree[root].son[2] != 0) {tree[tree[root].son[2]].ftr = root;} 
                        tree[x].son[1] = tree[x].son[2] = tree[x].size = tree[x].key = tree[x].tme = 0;
                    }   
        }
}

大概解释一下就是，每次把要删除的节点转到根，然后删掉，如果没有左子树，那么直接把右子树连上去，否则找到左子树的最大值，转到根，把右子树连到这个最大值上面（之前最大值一定没有右子树）。其实想想挺简单，但是结构体东西比较多所以比较乱。

第k值&查排名

直接套的SBT，基本没改。

int GetKth(int x,int k)
{  
    int s1 = tree[tree[x].son[1]].size;
    int s2 = tree[x].size - tree[tree[x].son[1]].size - tree[tree[x].son[2]].size;
    if (s1+1<=k&&k<=s1+s2) {int p = tree[x].key; splay(x); return p;}
    if(k > s1+s2) return GetKth(tree[x].son[2],k - s1 - s2);  
    else return GetKth(tree[x].son[1],k);  
} 

int GetRank(int x,int key)
{  
    int s1 = tree[tree[x].son[1]].size;
    int s2 = tree[x].size - tree[tree[x].son[1]].size - tree[tree[x].son[2]].size;
    if (key == tree[x].key) 
        {
            int p = 0;
            if (tree[x].son[1] == 0) p = 1; else p =  s1+1;
            splay(x); return p;
        }
    if(key < tree[x].key) return GetRank(tree[x].son[1],key);  
    if(key > tree[x].key) return GetRank(tree[x].son[2],key)+s1+s2; 
}

前驱和后继

终于到了最激动人心的时刻，展现splay伟大技巧的时候到了！
这里只以前驱为例。
每次查询x的前驱，首先插入x以免树中没有x，然后把x转到根，这时候左子树的最大值就是前驱！是不是很简单！
后继同理。

int pred(int key)
{
    insert(key);
    int k = search(root,key); splay(k);
    int res = extreme(tree[k].son[1],1);
    remove(root,key);
    return res;
}  

int succ(int key)
{
    insert(key);
    int k = search(root,key); splay(k);
    int res = extreme(tree[k].son[2],2);
    remove(root,key);
    return res;
}

完整代码

#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iomanip>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#define ll long long
#define inf 1000000000
#define mod 1000000007
#define N 3000000
#define ZIG rotate(x,2);
#define ZAG rotate(x,1);
#define ZIGZIG {rotate(y,2); rotate(x,2);}
#define ZAGZIG {rotate(x,1); rotate(x,2);}
#define ZAGZAG {rotate(y,1); rotate(x,1);}
#define ZIGZAG {rotate(x,2); rotate(x,1);} 
#define MMAX 1
#define MMIN 2
using namespace std;
struct TREE
{
    int ftr,son[3],key,tme,size;
} tree[N];
int root,tot,n,opt,i,x;
void rotate(int x,int w)//w=1左旋，w=2右旋
{
    int y = tree[x].ftr;
    tree[y].size = tree[y].size - tree[x].size + tree[tree[x].son[w]].size;
    tree[x].size = tree[x].size - tree[tree[x].son[w]].size + tree[y].size;
    tree[y].son[3-w] = tree[x].son[w];
    if (tree[x].son[w] != 0) tree[tree[x].son[w]].ftr = y;
    tree[x].ftr = tree[y].ftr;
    if (tree[y].ftr != 0)
        if (y == tree[tree[y].ftr].son[1]) tree[tree[y].ftr].son[1] = x;
            else tree[tree[y].ftr].son[2] = x;
    tree[y].ftr = x; tree[x].son[w] = y;
}

int search(int x,int key)
{
    int r = x;
    while (tree[r].key != key)
        {
            if (key < tree[r].key)
                {
                    if (tree[r].son[1] == 0) break;
                    r = tree[r].son[1];
                }   else
                {
                    if (tree[r].son[2] == 0) break;
                    r = tree[r].son[2];
                }
        }
    return r;
}

void splay(int x)
{
    while (tree[x].ftr != 0)
        {
            int y = tree[x].ftr;
            if (tree[y].ftr == 0)
                if (x == tree[y].son[1]) ZIG else ZAG
            else 
            if (tree[tree[y].ftr].son[1] == y)
                if (x == tree[y].son[1]) ZIGZIG else ZAGZIG
            else
                if (x == tree[y].son[2]) ZAGZAG else ZIGZAG
        }
    root = x;
}
void insert(int x)  
{
    bool flag; int u;
    if (tot == 0)  
    {  
        tot = 1; 
        tree[1].ftr = 0; tree[1].key = x;
        tree[1].size = tree[1].tme = root = 1; 
        return;  
    }  
    int k = search(root,x);  
    if (tree[k].key == x)  
    {  
        tree[k].tme++;
        u = k;  
        flag = true;  
    }  
    else  
    {  
        tot++;  
        tree[tot].key=x;  
        tree[tot].ftr=k;  
        tree[tot].size = tree[tot].tme = 1;  
        if (tree[k].key > x) tree[k].son[1] = tot;
                else tree[k].son[2] = tot;  
        flag = false;  
    }  
    while (k > 0)  
    {  
        tree[k].size++;  
        k = tree[k].ftr;  
    }  
    if (flag) splay(u); else splay(tot);  
}  

int extreme(int x,int w)  
{
    int k,tmp;
    k = x; while (tree[k].son[3-w] != 0) k = tree[k].son[3-w];
    tmp = tree[k].key;  
    splay(k);  
    return tmp;  
}  
void remove(int x,int key)
{
    if(key > tree[x].key) remove(tree[x].son[2],key);  
    else if(key < tree[x].key) remove(tree[x].son[1],key);  
    else
        {
            splay(x);
            if (tree[x].tme > 1) {tree[x].tme--; tree[x].size--;}
                else
                if (tree[x].son[1] == 0)
                    {
                        int y = tree[x].son[2];
                        tree[x].son[2] = tree[x].size = tree[x].key = tree[x].tme = 0;
                        root = y; tree[root].ftr = 0;
                    }   else
                    {
                        tree[tree[x].son[1]].ftr = 0;
                        int y = extreme(tree[x].son[1],MMAX);
                        tree[root].son[2] = tree[x].son[2];
                        tree[root].size = tree[root].size + tree[tree[x].son[2]].size;
                        if (tree[root].son[2] != 0) {tree[tree[root].son[2]].ftr = root;} 
                        tree[x].son[1] = tree[x].son[2] = tree[x].size = tree[x].key = tree[x].tme = 0;
                    }   
        }
}
int GetKth(int x,int k)
{  
    int s1 = tree[tree[x].son[1]].size;
    int s2 = tree[x].size - tree[tree[x].son[1]].size - tree[tree[x].son[2]].size;
    if (s1+1<=k&&k<=s1+s2) {int p = tree[x].key; splay(x); return p;}
    if(k > s1+s2) return GetKth(tree[x].son[2],k - s1 - s2);  
    else return GetKth(tree[x].son[1],k);  
} 

int GetRank(int x,int key)
{  
    int s1 = tree[tree[x].son[1]].size;
    int s2 = tree[x].size - tree[tree[x].son[1]].size - tree[tree[x].son[2]].size;
    if (key == tree[x].key) 
        {
            int p = 0;
            if (tree[x].son[1] == 0) p = 1; else p =  s1+1;
            splay(x); return p;
        }
    if(key < tree[x].key) return GetRank(tree[x].son[1],key);  
    if(key > tree[x].key) return GetRank(tree[x].son[2],key)+s1+s2; 
}  

int pred(int key)
{  
    insert(key);
    int k = search(root,key); splay(k);
    int res = extreme(tree[k].son[1],1);
    remove(root,key);
    return res;
}  

int succ(int key)
{  
    insert(key);
    int k = search(root,key); splay(k);
    int res = extreme(tree[k].son[2],2);
    remove(root,key);
    return res;
}  

int main()
{
    scanf("%d",&n);
    for (i = 1;i <= n; i++)
        {
            scanf("%d%d",&opt,&x);
            if (opt == 1) insert(x);
            if (opt == 2) remove(root,x);
            if (opt == 3) printf("%d\n",GetRank(root,x));
            if (opt == 4) printf("%d\n",GetKth(root,x));
            if (opt == 5) printf("%d\n",pred(x));
            if (opt == 6) printf("%d\n",succ(x));
        }
}