小学数学原理2：20 - 更多位的除法该怎么算？

摘要

本节是数学拓展课，主要讲解了多位数的除法计算方法。首先复习了除法的基本思想，即从高位开始分，若某一位不够分则换算成低位继续分。随后详细讲解了两位数除以一位数、三位数除以两位数以及四位数除以三位数的除法竖式计算过程，强调了试商的重要性，并通过具体例题演示了计算方法。最后总结了除法的核心思想，指出高位不够时换算低位继续分的统一标准流程，并鼓励学生通过多练习掌握这一核心能力。视频内容强调了理解和掌握除法竖式计算的统一思想，对于提升整数除法计算能力具有重要意义。

课程介绍与目标

1.介绍课程内容：更多位的除法计算方法。
2.目标：讲解多位数除以多位数的除法竖式计算。

除法竖式的复习

1.复习除法竖式的原理：从高位开始分。
2.整体分的思想：不够分时换成小单位继续分。

除法竖式的例题

1.例题1：58÷4，步骤：高位分一张十块，低位分18张一块。
2.例题2：58÷6，步骤：高位五张十块分给六人不够，直接看低位。
3.例题3：158÷12，步骤：高位一张百元换十张十元，低位分18张十元。
4.例题4：158÷18，步骤：高位一张百元换158张一元。

更高位的除法竖式

1.例题5：2940÷245，步骤：高位两张千元换294张十元。
2.例题6：1025÷205，步骤：高位一张千元换1025张一元。

除法竖式的统一思想

1.总结除法竖式的核心思想：高位不够时转换为低位继续分。
2.强调内功的重要性：掌握核心思想后能处理高位除法。

除法竖式的练习题

1.练习题1：2720÷32，步骤：高位两张千元换160张一元。
2.练习题2：9450÷210，步骤：高位九张千元换450张十元。
3.练习题3：11235÷321，步骤：高位十一张千元换160张十元。

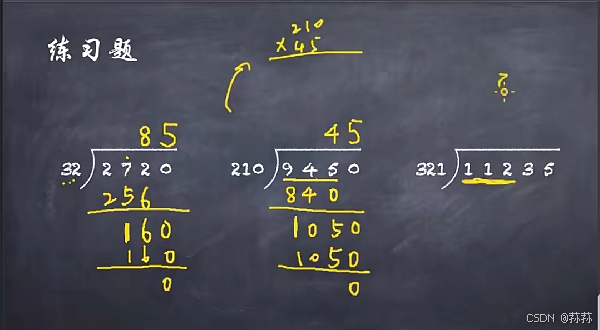
今天这节课呢，继续给大家来一节加星号的拓展课啊，算是我们关于乘除法这一部分的最后一节拓展课。更多为了除法该怎么算，我们之前也讲过除法的计算啊，但是我们讲除法竖式的时候只讲到多位数，除以两位数，对吧？就是比如说三位数，除以两位数这种，但如果更高位的除法，该怎么算呢？嗯，
这个我们在真正的教学过程中发现啊，很多同学其实是不会的。因为嗯，他他会说我只学过最多除以一位数或者除以两位数，后面怎么算？我怎么知道呢？所以说我们今天再把除法的思想给大家贯通一下。然后帮助大家去自己推理出更高级的除法。首先，我们来复习一下啊，因为这个东西毕竟还是几节课，之前的内容了。我们是怎么推理出除法竖式？大家还记得吗？就是从图形化的操作到除法竖式是中间有一么一个过渡过程的，
我们整体的那个分的思想，大家还记得吗？比如说这5858。怎么平均分给四个人呢？我们有一个整体思想叫从高位开始分啊，先分这个大的，比如说一人一张十块的，然后剩了一个十块的，怎么办呢？那这这个十块的没法分啊，我又不能撕开，就只好再换钱，对吧？所以有一个整体思想就是这样。多位数除以不管是除以一位数，
还是除以两位数啊？不需要什么特别的方法，你只需要从高位去开始分。如果高位儿某一位儿不够了，比如说剩一张没法分给四个人了，那这时