Simulation线性分析能代替非线性吗？一个简单实验告诉你答案

众所周知，有限元分析中的线性静力分析其实是对模型的一种简化分析，是在线性材料属性、小变形以及准静态加载条件前提条件下所做的一类仿真分析。而非线性分析则是包含材料非线性（如材料的塑性、超弹性等）、几何非线性（如大变形、大转动等）以及接触非线性（如部件之间的接触和摩擦）等情况，对模型进行的更准确的行为描述。

在SOLIDWORKS Simulation线性静力模块分析中，其实是可以使用“接触”定义的，从而可以进行一些“伪”非线性分析。

以下通过一个简单例子，来介绍下Simulation线性静力与非线性静力仿真分析对同一个模型仿真结果的影响。

示例模型如下图，由两块简单平板组成，两板之前存在一定的缝隙。

固定两板的左右两端，并在上部板的另一端施加一个向下的力，此力足够使两板接触并共同向下产生一定位移。

首先使用线性静力对该工况进行一次分析，得到应力与位移结果如下：

之后使用非线性分析对同一模型再次计算，得到应力与位移结果如下：

获得结果对比如下：

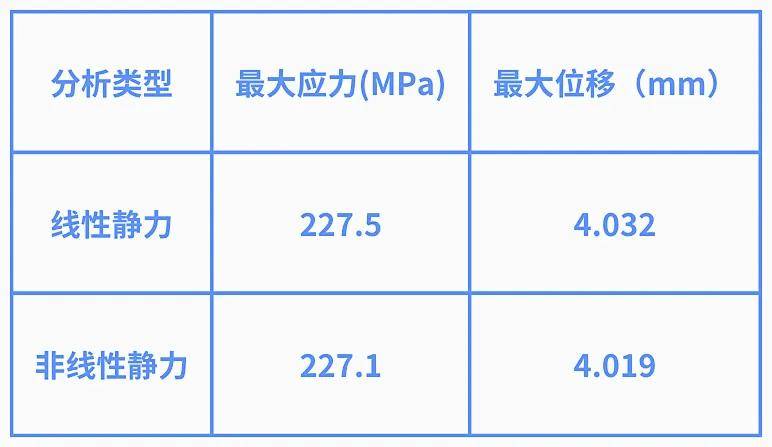
从结果对比上看，线性静力与非线性静力分析的结果非常接近，说明Simulation线性静力模块在处理接触非线性问题上还是值得一用的。

那么这两个结果区别在哪里呢？

我们通过查看两个结果的动画展示来揭开其真相。

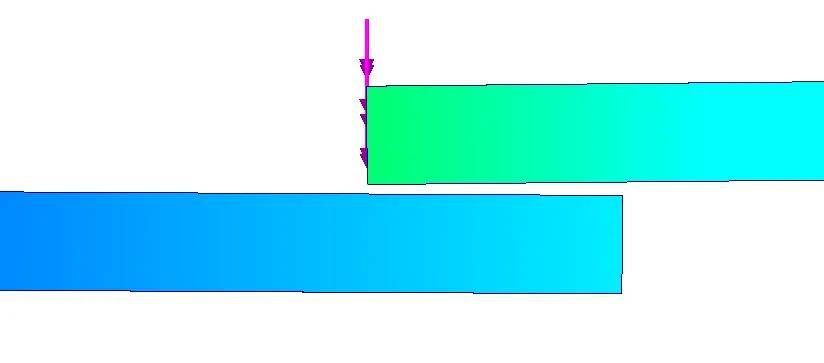
首先是线性静力的结果动画，截取开始时某帧，会发现，在两板还未接触时，下板就已经开始变形，并在最终一帧两板才接触在一起。

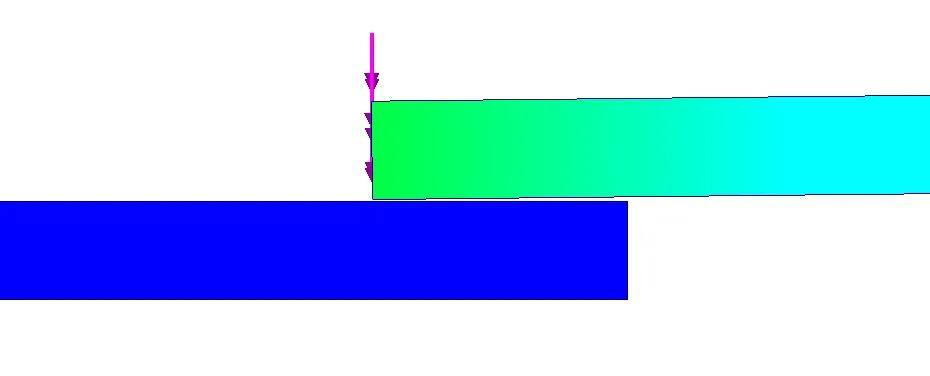
而使用非线性静力所得的结果动画显示，在两板未接触前，只有上板有变形输出，直到两板接触后，下板才可以发生形变，最终到达最终结果处。

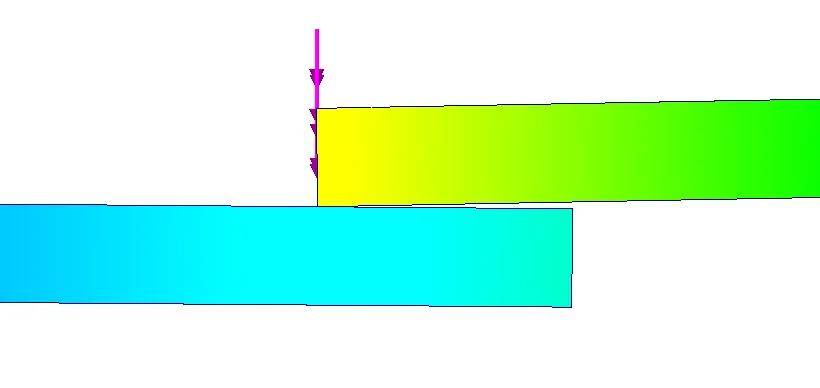
因此，对于部分涉及接触的算例，使用Simulation的线性静力模块也是同样可以得出有效结果，并且提高计算效率。

但是，当后处理过程需要涉及结果的中间过程时，使用线性静力无法获得中间过程的准确结果，此时就需要使用非线性分析来进行，从而获得过程结果。

附结果动画

Linear线性

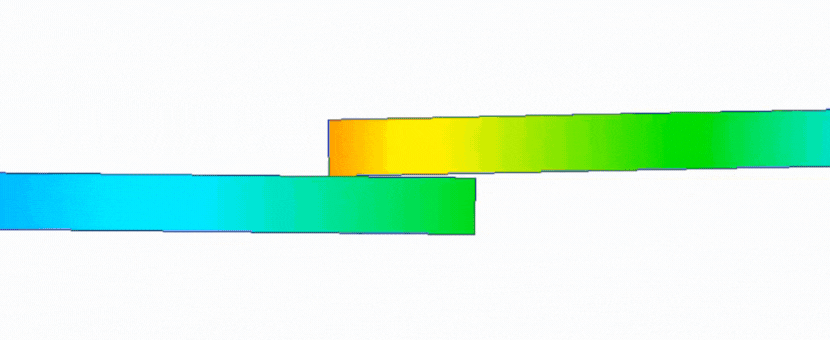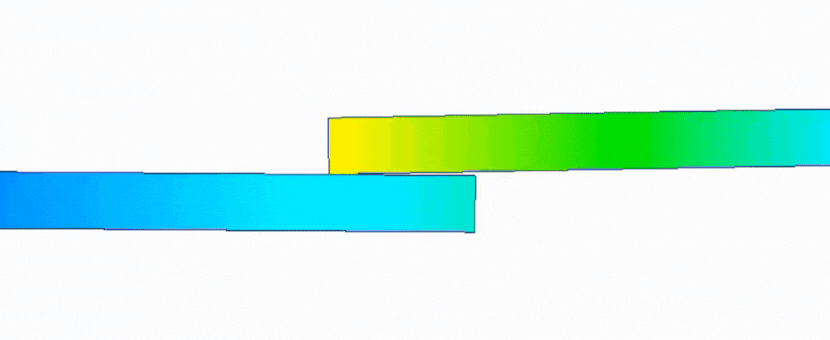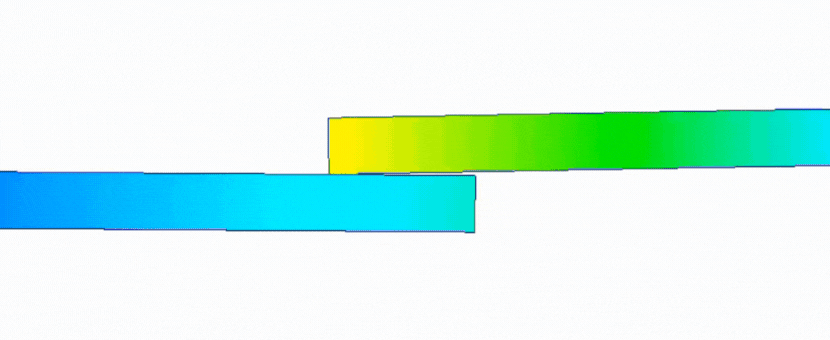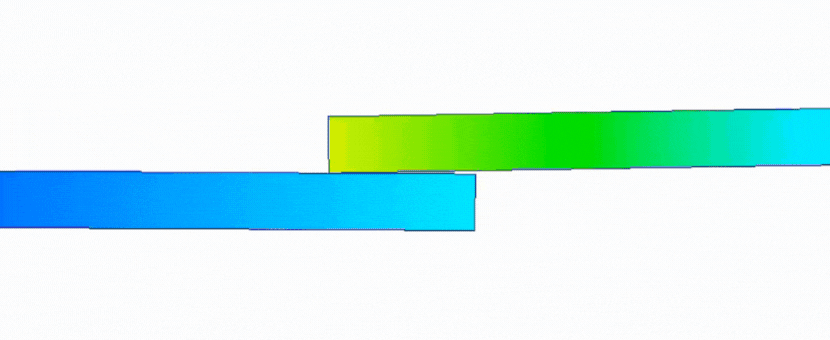
Nolinear非线性