基于Modelica的Stewart运动平台建模仿真

Stewart运动平台是一种利用6根直线驱动器，通过12个万向关节或虎克铰连接上下两个平台构成的运动机构。Stewart下平台作为并联运动机构的基座通常是静止的，通过调整6根直线驱动器的伸长量可以实现上平台的运动。Stewart平台已经在航空、航天、海底作业、地下开采、制造装配等行业有着广泛的应用。

本文基于Modelica语言对Stewart运动平台开展逆运动控制的建模仿真，分别从逆运动学、控制回路、永磁无刷电机控制、三维装配体模型转换为Modelica动力学模型几个方面介绍如何使用Modelica对Stewart平台进行建模仿真。

系统模型

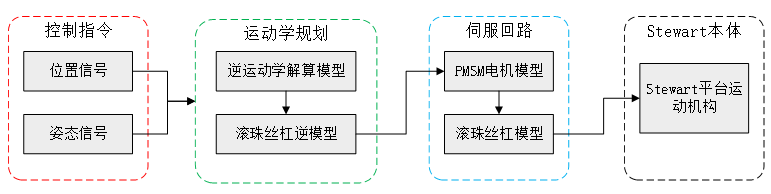
图1 Stewart平台系统架构

Stewart运动平台系统仿真模型主要由控制指令、运动学规划、伺服回路和Stewart本体四个部分组成。红色部分为控制指令模块，绿色部分为运动学规划模块，蓝色部分为伺服回路模块，灰色部分为Stewart本体模块。

如前文所述，Stewart运动平台可以实现六个自由度的运动，即上平台可以沿X-Y-Z方向进行平移运动，也可以绕X-Y-Z坐标轴进行旋转运动。控制指令根据Stewart上平台运动形式分为平移运动控制信号和旋转运动控制信号，如图2所示，控制指令设定运动平台的平移和旋转控制信号，并将控制信号传递给运动学规划模块进行逆运动学求解。

图2 Stewart平台系统模型

模型描述

逆运动学建模

Stewart运动平台的逆运动学是利用空间向量法根据期望的运动平台位置和姿态，求解各个直线作动器的伸长量，从而实现期望的运动平台位置和姿态。

如图3所示，Stewart上下平台有各自独立的坐标系，上平台坐标系为p-frame，下平台坐标系为b-frame。pi（i∈(1,6)）为上平台表示在p-frame坐标系下的6个铰接点，bi（i∈(1,6)）为下平台表示在b-frame坐标系下的6个铰接点。Stewart平台逆运动学的目标是求解向量的模长，从而确定各个直线驱动器的伸长量。

图3 Stewart平台简化原理图

下面利用空间向量法计算li（i∈(1,6)）。（注：所有参与计算的空间向量都要表示在b-frame坐标系下。）

方程（1）用于计算上平台6个铰接点在b-frame下的坐标，即qi（i∈(1,6)）向量。其中T表示p-frame坐标原地在b-frame的中的位置，Rpb是根据期望的姿态角得到的从p-frame到b-frame的旋转矩阵，作用是将pi向量从p-frame转换到b-frame。

由于bi，qi已知，利用方程（2）计算向量li，再利用方程（3）计算向量li的模长，减去直线驱动器的原始长度L0得到直线驱动的伸长量。

伺服电机控制回路设计

伺服电机作为驱动直线运动机构伸长或缩短的执行单元，是Stewart运动平台关键的被控对象。

本文中的伺服电机使用了PMSM永磁无刷电机，并利用串联PID控制方法实现电机的位置，角速度和电流的控制，控制回路框图如图4所示。

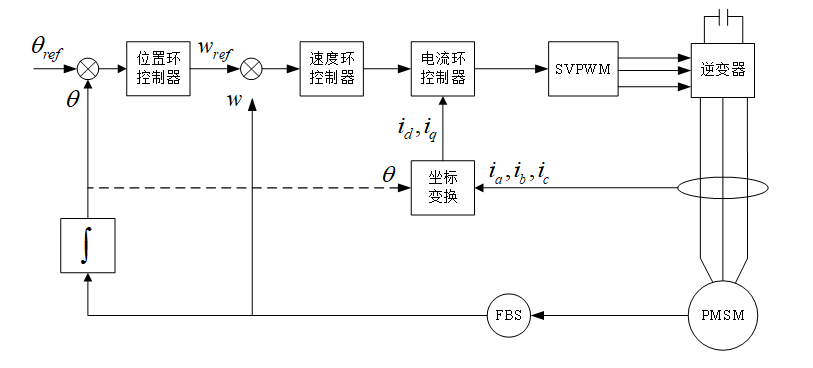
图4 PMSM电机的控制回路原理

如图5所示，伺服电机控制回路包括控制指令，控制器，伺服电机和传感器4个模块。其中控制器可以根据控制需求设置为位置控制模式或角速度控制模式。如图6和图7所示，控制模型可以根据使用需求选择位置控制模式或者角速度控制模式。

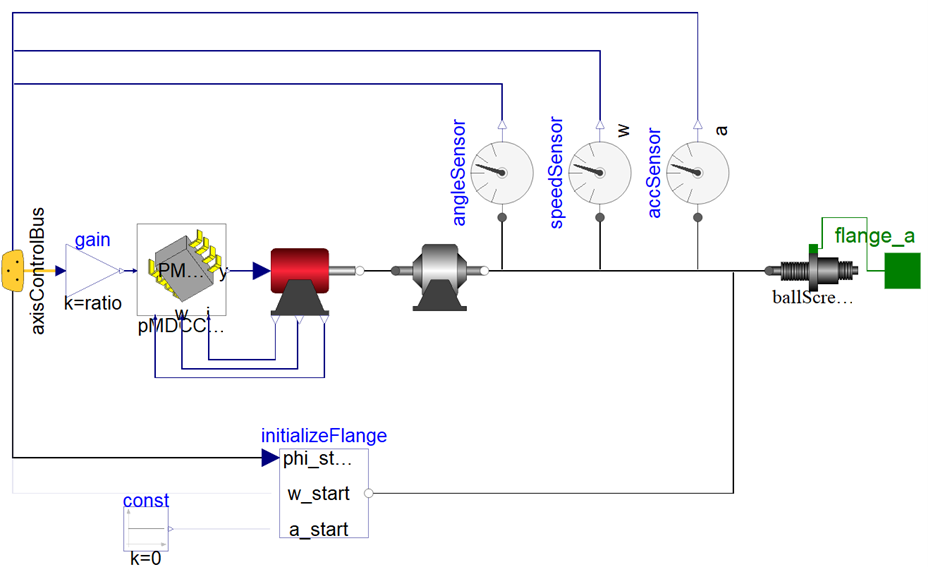
图5 伺服电机控制回路模型

图6 伺服电机控制器模型

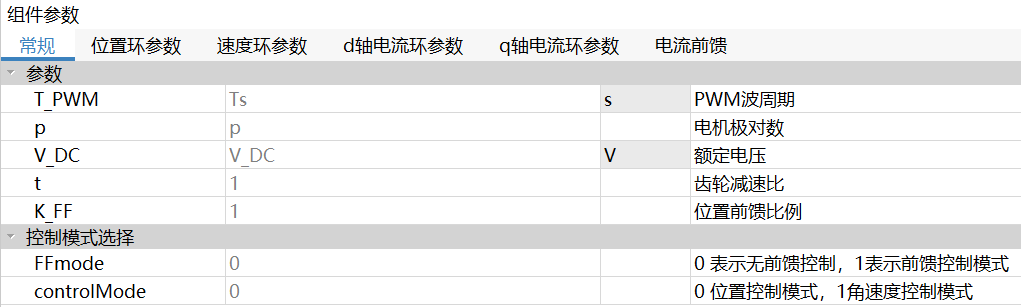
图7 电机控制器参数面板

在位置控制模式下，期望的角度控制信号与传感器反馈的角度信号作差得到的角度偏差信号经过位置控制器输出为角速度控制信号。如图8所示，位置控制器使用了抗积分饱和的PI控制器，根据实际电机的最大角速度对控制器输出信号进行限幅，防止积分器陷入饱和，导致系统超调与迟钝。

图8 电机位置控制器模型

期望角速度信号与传感器反馈的角速度信号作差得到的角速度误差信号作为角度控制器的输入信号。如图9所示，角速度控制器使用PI控制器，输出信号为期望的电机q轴电流，并根据电机的最大电流对输出信号进行限幅。

图9 电机角速度控制器模型

由于永磁无刷电机使用FOC算法，需要将电机三相交流电转化为直流电，利用电流控制器对直流电进行控制。（4）为Clark变换，将电机三相交流电转化为α，β静止坐标系下的交流电，然后利用Park变换（5），将α，β轴上的交流电转化到永磁无刷电机的d轴和q轴。

方程（6）表示电机q轴电动势平衡方程，方程（7）表示电机d轴电动势平衡方程，由方程（8）可知，电机输出扭矩与q轴电流成正比，为了保证电机能够产生最大的扭矩，所以令d轴电流为0，角速度控制器计算出的电流信号作为q轴电流控制信号。 

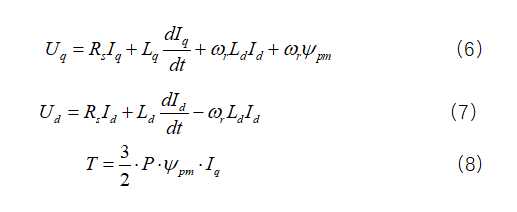
电流控制回路如图10所示，d轴期望的电流为0，与反馈的d轴电流作差得到d轴电流误差信号，经过d轴电流PI控制，输出d轴电压控制信号。角速度控制器输出的期望q轴电流与反馈的q轴电流作差得到的q轴电流误差信号作为q轴电流PI控制器的输入信号。考虑到电机电枢的反电动势造成的电压控制误差，在图10所示的电流控制回路中增加了电流控制的前馈补偿，用以消除电机反电动势扰动。

图10 电流控制模型

方程（9）为电机q轴补偿电压，其中为电机的电子转角，为电机d轴电流，为电机d轴电感，为电机磁通。方程（10）为电机d轴补偿电压，其中为电机q轴电流，为电机q轴电感。通过方程（9）和方程（10）对电流控制器计算的电压进行补偿可以有效的消除电机反电动势对电机控制产生扰动，提高电机的响应速度。

被控对象机械本体模型

图11为滚珠丝杠模型，用于将电机产生的回转运动转化为直线运动，带动上平台铰接点运动。

图11 滚珠丝杠模型

图12为滚珠丝杠逆模型，由图1的Stewart平台系统控制模型可知，逆运动学模块输出为位置信号，即各直线作动器的伸长量，滚珠丝杆逆模型可以将相应的直线位移信号转化为偏转角度信号传递给伺服电机模块。

图12 滚珠丝杠逆模型

通过三维装配体转换插件Kinetrans将SolidWorks中的装配体模型转换为Modelica运动学仿真模型如图13所示。Stewart平台包含6个并行的直线机构，每个直线机构两端通过万向节与平台铰接，中间的直线机构可以根据指令进行伸长或者缩短，最终实现上平台的运动。

图13 Stewart平台机械本体模型

仿真分析

图14为Stewart平台六根直线机构永磁无刷电机的角度和角速度控制响应曲线，其中控制指令为沿z轴正方向移动0.2m，俯仰角为15°，由控制响应曲线结果可知，Stewart上平台可以在规定时间内到达期望的姿态位置。

图14 Stewart平台控制响应曲线

图15为实际控制回路中Stewart平台的动画效果。从仿真结果可以看出，构建的Stewart运动平台系统模型能够按照给定的姿态进行运动，表明基于Modelica逆运动学控制Stewart运动平台系统模型满足系统控制要求。

图15 Stewart平台运动动画

本文基于Modelica语言建立的Stewart运动平台系统模型，融合了机械、电气、控制等多个学科，按照Stewart运动平台物理拓扑结构构建的系统模型更加符合实际情况，避免了对多学科耦合的人工解耦，突破了单一领域仿真软件只能对Stewart系统的某一特征进行仿真的局限性，可以更加全面、完整地表达系统整体特性，并且结合MWorks.Sysplorer软件丰富的模型库和工具箱，可以进一步对Stewart运动平台动力学、运动学和轨迹控制进行分析与优化。

原文链接：基于Modelica的Stewart运动平台建模仿真Stewart平台已经在航空、航天、海底作业、地下开采、制造装配等行业有着广泛的应用。https://mp.weixin.qq.com/s/_pCWOs0rUPJ9CM6tJUpFTQ