类SoftmaxWithLossLayer包含类SoftmaxLayer的实例。其中SoftmaxLayer层在正向传导函数中将64*10的bottom_data,通过计算得到64*10的top_data。这可以理解为输入数据为64个样本,每个样本特征数量为10,计算这64个样本分别在10个类别上的概率。公式如下,其中n=10,
f(zk)=ezk∑nezi=ezk−m∑nezi−m,m=max(zi)
SoftmaxWithLossLayer层利用SoftmaxLayer层的输出计算损失,公式如下,其中N为一个batch的大小(MNIST训练时batch_size为64,测试时batch_size为100)。 根据Cross-Entropy的定义有,
loss=−logf(zk)
反向传导时,计算偏导
loss=−logf(zk)=log(∑nezi)−zk
∂loss∂zj=⎧⎩⎨ezj∑nezi−1=f(zj)−1ezj∑nezi=f(zj)zj=zkzj≠zk
需要注意的一点是,在反向传导时SoftmaxWithLossLayer层并没有向正向传导时借用SoftmaxLayer层实现一部分,而是一手全部包办了。因此SoftmaxLayer::Backward_cpu()函数也就被闲置了。
如果网络在训练期间发散了,则最终计算结果accuracy ≈ 0.1(说明机器完全没有预测精度,纯靠蒙), loss ≈-log(0.1) = 2.3026。如果大家看见loss为2.3左右,就应该了解当前网络没有收敛,需要调节参数配置。至于怎么调节嘛,这往往就依赖经验了……
几个类的类关系图如下图所示,
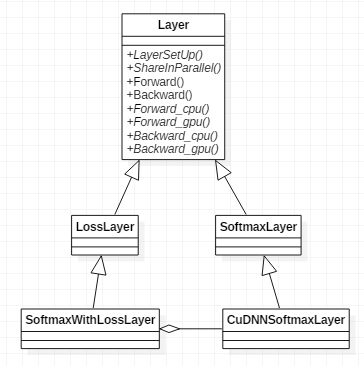
为了搞清楚传导的流程,我们首先看下SoftmaxLayer是如何工作的,头文件为softmax_layer.hpp
template <typename Dtype>
class SoftmaxLayer : public Layer<Dtype> {
public:
explicit SoftmaxLayer(const LayerParameter& param)
: Layer<Dtype>(param) {}
virtual void Reshape(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual inline const char* type() const { return "Softmax"; }
virtual inline int ExactNumBottomBlobs() const { return 1; }
virtual inline int ExactNumTopBlobs() const { return 1; }
protected:
virtual void Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Forward_gpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom);
virtual void Backward_gpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom);
int outer_num_;
int inner_num_;
int softmax_axis_;
Blob<Dtype> sum_multiplier_;
Blob<Dtype> scale_;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
这里的sum_multiplier_一样全部被初始化为1了的。而scale_的大小尺寸有点奇怪,在批处理的时候通常都会有num这个东西来表示数量,而scale又是单通道的。
大概是要将所有通道的数据的计算结果全部放在一起吧。
实现在softmax_layer.cpp文件中,
template <typename Dtype>
void SoftmaxLayer<Dtype>::Reshape(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
softmax_axis_ =
bottom[0]->CanonicalAxisIndex(this->layer_param_.softmax_param().axis());
top[0]->ReshapeLike(*bottom[0]);
vector<int> mult_dims(1, bottom[0]->shape(softmax_axis_));
sum_multiplier_.Reshape(mult_dims);
Dtype* multiplier_data = sum_multiplier_.mutable_cpu_data();
caffe_set(sum_multiplier_.count(), Dtype(1), multiplier_data);
outer_num_ = bottom[0]->count(0, softmax_axis_);
inner_num_ = bottom[0]->count(softmax_axis_ + 1);
vector<int> scale_dims = bottom[0]->shape();
scale_dims[softmax_axis_] = 1;
scale_.Reshape(scale_dims);
}
template <typename Dtype>
void SoftmaxLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
const Dtype* bottom_data = bottom[0]->cpu_data();
Dtype* top_data = top[0]->mutable_cpu_data();
Dtype* scale_data = scale_.mutable_cpu_data();
int channels = bottom[0]->shape(softmax_axis_);
int dim = bottom[0]->count() / outer_num_;
caffe_copy(bottom[0]->count(), bottom_data, top_data);
for (int i = 0; i < outer_num_; ++i) {
caffe_copy(inner_num_, bottom_data + i * dim, scale_data);
for (int j = 0; j < channels; j++) {
for (int k = 0; k < inner_num_; k++) {
scale_data[k] = std::max(scale_data[k],
bottom_data[i * dim + j * inner_num_ + k]);
}
}
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels, inner_num_,
1, -1., sum_multiplier_.cpu_data(), scale_data, 1., top_data);
caffe_exp<Dtype>(dim, top_data, top_data);
caffe_cpu_gemv<Dtype>(CblasTrans, channels, inner_num_, 1.,
top_data, sum_multiplier_.cpu_data(), 0., scale_data);
for (int j = 0; j < channels; j++) {
caffe_div(inner_num_, top_data, scale_data, top_data);
top_data += inner_num_;
}
}
}
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
从代码中可以看到,反向的时候,批处理中每个图像是分别处理的:
先将某个图像按照通道维度计算最大值,存入scale_data中,所以感觉上scale_data只需要height*width大小的存储空间就够了,但是实际上却开辟了num*height*width。
这里的反向计算过程中可能与斯坦福的介绍稍微有点差别,不过原理上都是一样的,这里的反向计算如下:
假设某一个图像在某一个(channel, height, width)的坐标上的数据为x,在通道(channel, :, :)上的最大值为x_max;
在for后面的两个小for里面就是计算这个x_max;
之后的计算可以理解成遍历该通道的所有数据:(实际上是所有通道一起计算的)
之后再计算: x - x_max;
再之后计算指数:exp(x-x_max);
在求和这些指数:sum(x: exp(x-x_max));
最后再用除法,即:
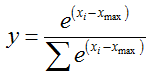
在源码中解释道了为什么要减去最大值,这是因为避免所谓的“数值问题”,那么到底是什么问题呢?我们知道指数函数是一个严格递增的函数,如果直接使用x的话,可能会造成大数吃小数的问题,因为sum的分母会因为某一个x很大而整体很大,其余的很多小x都会因此变得非常小。估计源码中说到的就是这个问题吧。
整个反向过程看完了,还是不明白为啥scale_data开辟的空间会比实际使用的大很多呢?
template <typename Dtype>
void SoftmaxLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down,
const vector<Blob<Dtype>*>& bottom) {
const Dtype* top_diff = top[0]->cpu_diff();
const Dtype* top_data = top[0]->cpu_data();
Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
Dtype* scale_data = scale_.mutable_cpu_data();
int channels = top[0]->shape(softmax_axis_);
int dim = top[0]->count() / outer_num_;
caffe_copy(top[0]->count(), top_diff, bottom_diff);
for (int i = 0; i < outer_num_; ++i) {
for (int k = 0; k < inner_num_; ++k) {
scale_data[k] = caffe_cpu_strided_dot<Dtype>(channels,
bottom_diff + i * dim + k, inner_num_,
top_data + i * dim + k, inner_num_);
}
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels, inner_num_, 1,
-1., sum_multiplier_.cpu_data(), scale_data, 1., bottom_diff + i * dim);
}
caffe_mul(top[0]->count(), bottom_diff, top_data, bottom_diff);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
反向的过程其实很优雅,说优雅是因为softmax本身就非常优雅,看似很复杂的函数表达式,导数的计算确实非常的简便:
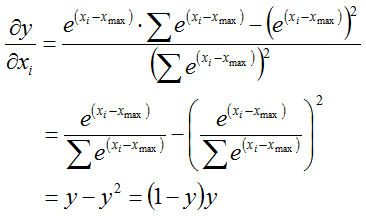
所以,误差传递过程是:
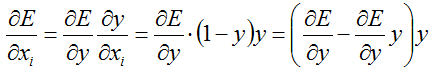
这个误差传递的过程,也是源码的计算思路过程:
先直接将top_diff存入bottom_diff中;
再计算这个误差与top_data的乘积存放在scale_data中;
在计算误差减掉scale_data,还是存放在bottom_diff中;
最后再计算bottom_diif与top_data的乘积,存入bottom_diff中。
再回过来看SoftmaxWithLossLayer的源代码,先看一下它的基类LossLayer是如何实现的。
template <typename Dtype>
class LossLayer : public Layer<Dtype> {
public:
explicit LossLayer(const LayerParameter& param)
: Layer<Dtype>(param) {}
virtual void LayerSetUp(
const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top);
virtual void Reshape(
const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top);
virtual inline int ExactNumBottomBlobs() const { return 2; }
virtual inline bool AutoTopBlobs() const { return true; }
virtual inline int ExactNumTopBlobs() const { return 1; }
virtual inline bool AllowForceBackward(const int bottom_index) const {
return bottom_index != 1;
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
cpp实现如下,
template <typename Dtype>
void LossLayer<Dtype>::LayerSetUp(
const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top) {
if (this->layer_param_.loss_weight_size() == 0) {
this->layer_param_.add_loss_weight(Dtype(1));
}
}
template <typename Dtype>
void LossLayer<Dtype>::Reshape(
const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top) {
CHECK_EQ(bottom[0]->num(), bottom[1]->num())
<< "The data and label should have the same number.";
vector<int> loss_shape(0);
top[0]->Reshape(loss_shape);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
再看一下子类SoftmaxWithLossLayer的实现,
template <typename Dtype>
class SoftmaxWithLossLayer : public LossLayer<Dtype> {
public:
explicit SoftmaxWithLossLayer(const LayerParameter& param)
: LossLayer<Dtype>(param) {}
virtual void LayerSetUp(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Reshape(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual inline const char* type() const { return "SoftmaxWithLoss"; }
virtual inline int ExactNumTopBlobs() const { return -1; }
virtual inline int MinTopBlobs() const { return 1; }
virtual inline int MaxTopBlobs() const { return 2; }
protected:
virtual void Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Forward_gpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom);
virtual void Backward_gpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom);
virtual Dtype get_normalizer(
LossParameter_NormalizationMode normalization_mode, int valid_count);
shared_ptr<Layer<Dtype> > softmax_layer_;
Blob<Dtype> prob_;
vector<Blob<Dtype>*> softmax_bottom_vec_;
vector<Blob<Dtype>*> softmax_top_vec_;
bool has_ignore_label_;
int ignore_label_;
LossParameter_NormalizationMode normalization_;
int softmax_axis_, outer_num_, inner_num_;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
softmax_loss_layer.cpp定义如下,
template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::LayerSetUp(
const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top) {
LossLayer<Dtype>::LayerSetUp(bottom, top);
LayerParameter softmax_param(this->layer_param_);
softmax_param.set_type("Softmax");
softmax_layer_ = LayerRegistry<Dtype>::CreateLayer(softmax_param);
softmax_bottom_vec_.clear();
softmax_bottom_vec_.push_back(bottom[0]);
softmax_top_vec_.clear();
softmax_top_vec_.push_back(&prob_);
softmax_layer_->SetUp(softmax_bottom_vec_, softmax_top_vec_);
has_ignore_label_ =
this->layer_param_.loss_param().has_ignore_label();
if (has_ignore_label_) {
ignore_label_ = this->layer_param_.loss_param().ignore_label();
}
if (!this->layer_param_.loss_param().has_normalization() &&
this->layer_param_.loss_param().has_normalize()) {
normalization_ = this->layer_param_.loss_param().normalize() ?
LossParameter_NormalizationMode_VALID :
LossParameter_NormalizationMode_BATCH_SIZE;
} else {
normalization_ = this->layer_param_.loss_param().normalization();
}
}
template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::Reshape(
const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top) {
LossLayer<Dtype>::Reshape(bottom, top);
softmax_layer_->Reshape(softmax_bottom_vec_, softmax_top_vec_);
softmax_axis_ =
bottom[0]->CanonicalAxisIndex(this->layer_param_.softmax_param().axis());
outer_num_ = bottom[0]->count(0, softmax_axis_);
inner_num_ = bottom[0]->count(softmax_axis_ + 1);
CHECK_EQ(outer_num_ * inner_num_, bottom[1]->count())
<< "Number of labels must match number of predictions; "
<< "e.g., if softmax axis == 1 and prediction shape is (N, C, H, W), "
<< "label count (number of labels) must be N*H*W, "
<< "with integer values in {0, 1, ..., C-1}.";
if (top.size() >= 2) {
top[1]->ReshapeLike(*bottom[0]);
}
}
template <typename Dtype>
Dtype SoftmaxWithLossLayer<Dtype>::get_normalizer(
LossParameter_NormalizationMode normalization_mode, int valid_count) {
Dtype normalizer;
switch (normalization_mode) {
case LossParameter_NormalizationMode_FULL:
normalizer = Dtype(outer_num_ * inner_num_);
break;
case LossParameter_NormalizationMode_VALID:
if (valid_count == -1) {
normalizer = Dtype(outer_num_ * inner_num_);
} else {
normalizer = Dtype(valid_count);
}
break;
case LossParameter_NormalizationMode_BATCH_SIZE:
normalizer = Dtype(outer_num_);
break;
case LossParameter_NormalizationMode_NONE:
normalizer = Dtype(1);
break;
default:
LOG(FATAL) << "Unknown normalization mode: "
<< LossParameter_NormalizationMode_Name(normalization_mode);
}
return std::max(Dtype(1.0), normalizer);
}
template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::Forward_cpu(
const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top) {
softmax_layer_->Forward(softmax_bottom_vec_, softmax_top_vec_);
const Dtype* prob_data = prob_.cpu_data();
const Dtype* label = bottom[1]->cpu_data();
int dim = prob_.count() / outer_num_;
int count = 0;
Dtype loss = 0;
for (int i = 0; i < outer_num_; ++i) {
for (int j = 0; j < inner_num_; j++) {
const int label_value = static_cast<int>(label[i * inner_num_ + j]);
if (has_ignore_label_ && label_value == ignore_label_) {
continue;
}
DCHECK_GE(label_value, 0);
DCHECK_LT(label_value, prob_.shape(softmax_axis_));
loss -= log(std::max(prob_data[i * dim + label_value * inner_num_ + j],
Dtype(FLT_MIN)));
++count;
}
}
top[0]->mutable_cpu_data()[0] = loss / get_normalizer(normalization_, count);
if (top.size() == 2) {
top[1]->ShareData(prob_);
}
}
template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom) {
if (propagate_down[1]) {
LOG(FATAL) << this->type()
<< " Layer cannot backpropagate to label inputs.";
}
if (propagate_down[0]) {
Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
const Dtype* prob_data = prob_.cpu_data();
caffe_copy(prob_.count(), prob_data, bottom_diff);
const Dtype* label = bottom[1]->cpu_data();
int dim = prob_.count() / outer_num_;
int count = 0;
for (int i = 0; i < outer_num_; ++i) {
for (int j = 0; j < inner_num_; ++j) {
const int label_value = static_cast<int>(label[i * inner_num_ + j]);
if (has_ignore_label_ && label_value == ignore_label_) {
for (int c = 0; c < bottom[0]->shape(softmax_axis_); ++c) {
bottom_diff[i * dim + c * inner_num_ + j] = 0;
}
} else {
bottom_diff[i * dim + label_value * inner_num_ + j] -= 1;
++count;
}
}
}
Dtype loss_weight = top[0]->cpu_diff()[0] /
get_normalizer(normalization_, count);
caffe_scal(prob_.count(), loss_weight, bottom_diff);
}
}
反向传导时,计算偏导
loss=−logf(zk)=log(∑nezi)−zk
∂loss∂zj=⎧⎩⎨ezj∑nezi−1=f(zj)−1ezj∑nezi=f(zj)zj=zkzj≠zk
需要注意的一点是,在反向传导时SoftmaxWithLossLayer层并没有向正向传导时借用SoftmaxLayer层实现一部分,而是一手全部包办了。因此SoftmaxLayer::Backward_cpu()函数也就被闲置了。









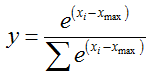
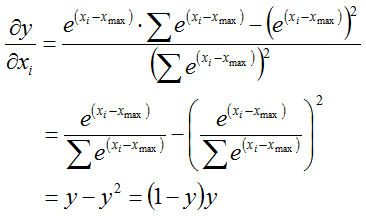
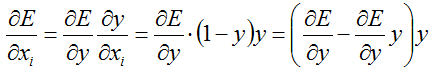














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








