
英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用
目录
2.4. Data-Dependent Wavelet Attention
2.4.1. Wavelet-based Frequency Analysis
2.4.2. Data-dependent Wavelet Attention for Dynamic Frequency Analysis
2.5. Dynamic Time Warping Attention
2.5.2. Local Dynamic Time Warping Attentions
2.6.1. Task I: Time Series Classification
2.6.2. Task II:Time Series Forecasting
3.1. dynamic time warping (DTW)
1. 心得
(1)真的非常讨厌用莫名其妙花体写论文的人。有些花体首先是根本不认识,其次是公式识别容易识别成别的字母,再其次是CSDN不支持那种类型的花体。都是看分析了干嘛要这么花里胡哨的?能不能不要扭来扭去?
![]()
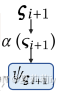
(2)吐槽归吐槽,不要上升到文章。好吧,作者把原本机器学习的DTW迁移到了深度学习,挺好的做法
2. 论文逐段精读
2.1. Abstract
①Challenge in time series analysis: heterogeneity of data
②Two types of heterogeneity: intra-sequence nonstationarity (I NAME it ISN) and inter-sequence asynchronism (and I NAME it ISA)(作者总是写全称太长了我靠我手打不容易啊)
③Solution: proposed a WHEN framework which contains 2 attention mechanims
asynchronism n. 不同时;异步性
2.2. Introduction
①Task types for time series analysis (TSA): time series classification (TSC) and time series forecasting (TSF)
②ISN attributes to inherently heterogeneous, such as mean, variance, frequency components, etc. And ISA is due to heterogeneous sampling rate or phase perturbation. They often solved by Dynamic time Warping (DTW) algorithm, but it's not deep learning method
③Taking ECG as example, the intra-sequence nonstationarity and inter-sequence asynchronism are like:

④Limitations of CNN and RNN on two hetero characters: the structures of deep model are repetitive(作者觉得重复的卷积核不能预测异质的东西,不过现在很多也不用普通卷积了嘛)
⑤Framework of Wavelet-DTW Hybrid attEntion Networks (WHEN):

2.3. Related Work
(1)Heterogeneous Time Series Analysis
①Traditional way: manually transform non-stationary time series to stationary
②Lists other DL methods
(2)Time Series Classification (TSC)
①3 types of methods: distance based methods, feature based methods and ensemble methods
(3)TimeSeriesForecasting(TSF)
①TFS relies on autoregressive correlation
2.4. Data-Dependent Wavelet Attention
2.4.1. Wavelet-based Frequency Analysis
①Define a mother wavelet function:
where denotes dilated scalar (frequency band),
is shift
②For sequential signal and base
, the WT is:
where is component intensity of frequency band
at location
2.4.2. Data-dependent Wavelet Attention for Dynamic Frequency Analysis
①They design a data-dependent wavelet attention mechanism (WaveAtt):

②The original input: a multivariate time series , where
denotes
dimensional vector
③They encode by Bidirectional Long Short Term Memory (BiLSTM) to hidden sequence
, it can capture the forward and backward temporal dependencies
④The input of WaveAtt: where
denotes dimension
⑤Through sliding window of length , an example sequence cetered on time step
:
⑥And they set
where are trainable parameters,
is a small value,
is positive
⑦Data-dependent wavelet function:
compared to common WT, fixed is replaced by
and
⑧The attention weights:
⑨The output of BiLSTM:
⑩To get diverse frequency components, they introduce wavelet families, in time step
, the frequency components are:
⑪The final output of WaveAtt:
2.5. Dynamic Time Warping Attention
2.5.1. Dynamic Time Warping
①For two sequences, and
, Dynamic Time Warping (DTW) calculates:
where ,
,
,
,
②The distance between two sequences:
where denotes L2 Norm
③The shortest distance between two sequences lies in all the possible warping path
:
where is the similarity measurement
④⭐The non-linear alignment method allow the pair contains different temporal indexes but the same order index, such as and
⑤Furthermore, DTW allows two unequal length sequences, for instance, a sequence and its down sampling sequence
2.5.2. Local Dynamic Time Warping Attentions
①Generate vector sequence by
through task-dependent neural network, where the dimension of
is
②Define a learnable Universal Feature (vector) sequence , it has the same dimension as
③The schematic of DTWAtt:

where the window size is , the example subsequence is
, and they got the
at the same length, the distances of all possible warping paths between they two are:
④Attention weight of each warping path:
⑤The summed distance:
⑥For parameter sequences
, the output of multi head DTWAtt is
2.5.3. The Model Output Layer
①TSC and TSF:

where Conv1D,128,3 denotes 128 conv kernels with 3 kernel size
2.6. Experiments
2.6.1. Task I: Time Series Classification
(1)Datasets
①Input: multivariate time series
②Datasets: 30 datasets from UEA multivariate time series classification
③Sample size: 24-50000
④Series length: 8-17984
⑤Dimension: 2-1345
(2)Baselines
①这八个baseline直接写了一页啊, they introduced a DTW-based algorithm, a patternbased algorithm, a feature-based algorithm, two ensemble methods, two deep learning models, and a wavelet-based deep learning model
②Baselines: DTW𝐷, WEASEL+MUSE, CMFMTS+RF, LCEM, TapNet, TST, MINIROCKET, mWDN and two variants of WHEN
(3)Results and Analysis
①Comparison table:

②Nemenyi test on compared models:

where difference beyonds CD on the top left denotes statistically significant difference, blue lines are WHEN and its variants, reds are DL models and oranges are traditional baselines
2.6.2. Task II:Time Series Forecasting
(1)Datasets
①Temperature: 50 dimensional time series with length of 164
②AQI: 6 dimensional time series with length of 2815
③Traffic: 214 dimensional time series with length of 4464
(2)Baselines
①Compared baselines: ARIMA, FC-LSTM, NRDE, STRIPE++, ESG, GTS, TST, mWDN, and two variants of WHEN
(3)Results and Analysis
①Comparison table:

2.6.3. Exploratory Analysis
(1)Data-Dependent Frequencies Extraction
①Data-dependent frequencies extracted by different wavelet families:

(2)Warping Distance Comparison in DTW Attention
①DWT vis:

2.7. Conclusion
good good
3. 知识补充
3.1. dynamic time warping (DTW)
(1)定义:DTW允许通过非线性时间轴的拉伸和压缩来匹配序列,从而度量它们之间的相似度。与欧几里得距离等直接度量方法不同,DTW能够处理时序信号中的非线性时间变化,即它允许不同步或不对齐的序列进行相似性度量。DTW的本质是通过“动态规划”技术,在两条时间序列之间寻找一种最优的对齐路径,以最小化它们的距离。
(2)参考学习:DTW(Dynamic Time Warping)动态时间规整 - 知乎
3.2. Nemenyi test
(1)参考学习:非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验_nemenyi检验-CSDN博客
4. Reference
Wang, J. et al. (2023) 'WHEN: A Wavelet-DTW Hybrid Attention Network for Heterogeneous Time Series Analysis', KDD, pp. 2361-2373. doi: WHEN: A Wavelet-DTW Hybrid Attention Network for Heterogeneous Time Series Analysis | Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








