图解AI数学基础(1) | 线性代数与矩阵论（要点速查清单·完结）

• 作者：韩信子@ShowMeAI
• 教程地址：https://www.showmeai.tech/tutorials/83
• 本文地址：https://www.showmeai.tech/article-detail/162
• 声明：版权所有，转载请联系平台与作者并注明出处

---

1.标量（Scalar）

一个标量就是一个单独的数。只具有数值大小，没有方向（部分有正负之分），运算遵循一般的代数法则。

• 一般用小写的变量名称表示。
• 质量 $m$、速率 $v$、时间 $t$、电阻 $\rho$ 等物理量，都是数据标量。

2.向量（Vector）

向量指具有大小和方向的量，形态上看就是一列数。

• 通常赋予向量粗体小写的名称；手写体则在字母上加一个向右的箭头。
• 向量中的元素是有序排列的，通过索引可以确定每个元素。
• 以下两种方式，可以明确表示向量中的元素时（注意用方括号）。
• 可以把向量看作空间中的有向线段，向量的每个组成元素，对应向量在不同的坐标轴上的投影长度。

AI中的应用：在机器学习中，单条数据样本的表征都是以向量化的形式来完成的。向量化的方式可以帮助AI算法在迭代与计算过程中，以更高效的方式完成。

3.矩阵（Matrix）

矩阵是二维数组，其中的每一个元素被两个索引确定。矩阵在机器学习中至关重要，无处不在。

• 通常会赋予矩阵粗体大写的变量名称。

AI中的应用：样本以矩阵形态表示： $m$ 条数据/样本，$n$ 个特征的数据集，就是一个 $m\times n$ 的矩阵。

4.张量（Tensor）

几何代数中定义的张量，是基于向量和矩阵的推广。

• 标量，可以视为零阶张量
• 向量，可以视为一阶张量
• 矩阵，可以视为二阶张量

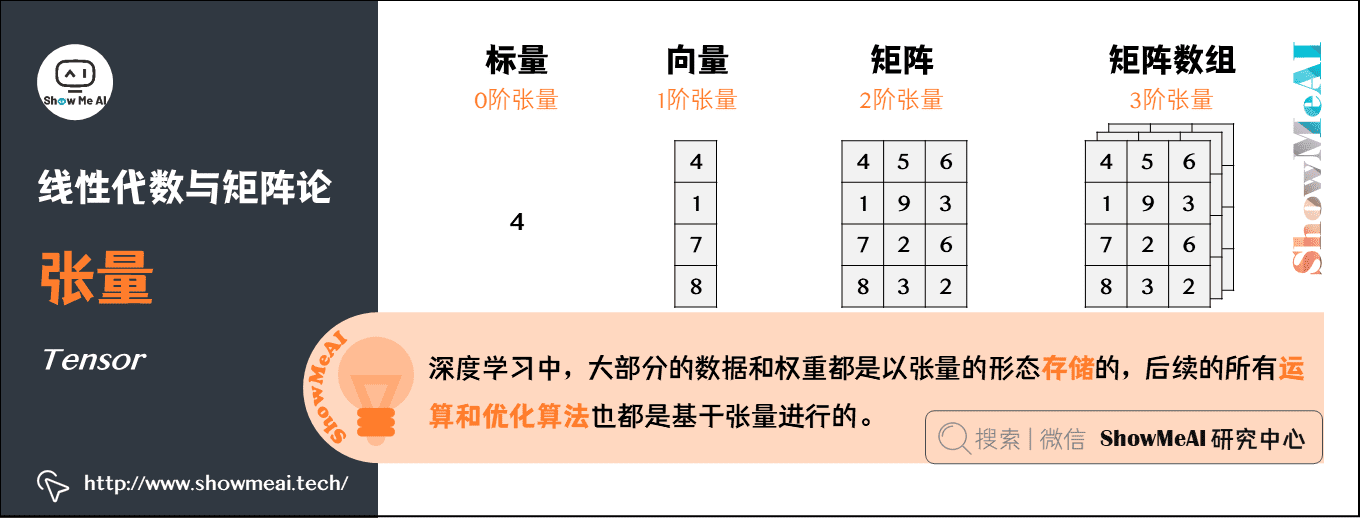
• 图片以矩阵形态表示：将一张彩色图片表示成一个 $H\times W\times C$ 的三阶张量，其中 $H$ 是高， $W$ 是宽，$C$ 通常取 $3$，表示彩色图 $3$ 个颜色通道。
• 在这个例子的基础上，将这一定义继续扩展，即：用四阶张量（样本，高度，宽度，通道）表示一个包含多张图片的数据集，其中，样本表示图片在数据集中的编号。
• 用五阶张量（样本，帧速，高度，宽度，通道）表示视频。

AI中的应用：张量是深度学习中一个非常重要的概念，大部分的数据和权重都是以张量的形态存储的，后续的所有运算和优化算法也都是基于张量进行的。

5.范数（Norm）

范数是一种强化了的距离概念；简单来说，可以把『范数』理解为『距离』。

在数学上，范数包括『向量范数』和『矩阵范数』：

• 向量范数（Vector Norm），表征向量空间中向量的大小。向量空间中的向量都是有大小的，这个大小就是用范数来度量。不同的范数都可以来度量这个大小，就好比米和尺都可以来度量远近一样。
• 矩阵范数（Matrix Norm），表征矩阵引起变化的大小。比如，通过运算 $\mathbf{A}\mathbf{X}=\mathbf{B}$，可以将向量 $\mathbf{X}$ 变化为 $\mathbf{B}$ ，矩阵范数就可以度量这个变化的大小。

向量范数的计算：

对于 $\mathrm{p}-$ 范数，如果 $\mathbf{x}={\left[x_1,x_2,\cdots ,x_n\right]}^{\mathrm{T}}$，那么向量 $\mathbf{x}$ 的 $\mathrm{p}-$ 范数就是 $\Vert \mathbf{x}{\Vert }_p={\left({\left|x_1\right|}^p+{\left|x_2\right|}^p+\cdots +{\left|x_n\right|}^p\right)}^{\frac{1}{p}}$。

L1范数：$||\mathbf{x}|{|}_1=\left|x_1\right|+\left|x_2\right|+\left|x_3\right|+\cdots +\left|x_n\right|$

• $\mathrm{p}=1$ 时，就是 L1 范数，是 $\mathbf{x}$ 向量各个元素的绝对值之和。
• L1 范数有很多的名字，例如我们熟悉的曼哈顿距离、最小绝对误差等。

L2范数：$\Vert \mathbf{x}{\Vert }_2={\left({\left|x_1\right|}^2+{\left|x_2\right|}^2+{\left|x_3\right|}^2+\cdots +{\left|x_n\right|}^2\right)}^{1/2}$

• $\mathrm{p}=2$ 时，就是 L2 范数，是 $\mathbf{x}$ 向量各个元素平方和的开方。
• L2 范数是我们最常用的范数，欧氏距离就是一种 L2 范数。

AI中的应用：在机器学习中，L1范数和L2范数很常见，比如『评估准则的计算』、『损失函数中用于限制模型复杂度的正则化项』等。

6.特征分解（Eigen-decomposition）

将数学对象分解成多个组成部分，可以找到他们的一些属性，或者能更高地理解他们。例如，整数可以分解为质因数，通过 $12=2\times 3\times 3$ 可以得到『$12$ 的倍数可以被 $3$ 整除，或者 $12$ 不能被 $5$ 整除』。

同样，我们可以将『矩阵』分解为一组『特征向量』和『特征值』，来发现矩阵表示为数组元素时不明显的函数性质。特征分解（Eigen-decomposition）是广泛使用的矩阵分解方式之一。

• 特征向量：方阵 $\mathbf{A}$ 的特征向量，是指与 $\mathbf{A}$ 相乘后相当于对该向量进行缩放的非零向量，即 $\mathbf{A}\nu =\lambda \nu$ 。

• 特征值：标量 $\lambda$ 被称为这个特征向量对应的特征值。

使用特征分解去分析矩阵 $\mathbf{A}$ 时，得到特征向量 $\nu$ 构成的矩阵 $\mathbf{Q}$ 和特征值构成的向量 $\mathbf{\Lambda }$ ，我们可以重新将 $\mathbf{A}$ 写作： $\mathbf{A}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{-1}$

7.奇异值分解（Singular Value Decomposition，SVD）

矩阵的特征分解是有前提条件的。只有可对角化的矩阵，才可以进行特征分解。实际很多矩阵不满足这一条件，这时候怎么办呢？

将矩阵的『特征分解』进行推广，得到一种被称为『矩阵的奇异值分解』的方法，即将一个普通矩阵分解为『奇异向量』和『奇异值』。通过奇异值分解，我们会得到一些类似于特征分解的信息。

将矩阵 $\mathbf{A}$ 分解成三个矩阵的乘积 $\mathbf{A}=\mathbf{U}\mathbf{D}{\mathbf{V}}^{-1}$ 。

• 假设 $\mathbf{A}$ 是一个 $m\times n$ 矩阵，那么 $\mathbf{U}$ 是一个 $m\times m$ 矩阵， $D$ 是一个 $m\times n$ 矩阵， $V$ 是一个 $n\times n$ 矩阵。

• $\mathbf{U}\mathbf{V}\mathbf{D}$ 这几个矩阵都拥有特殊的结构：

  • $\mathbf{U}$ 和 $\mathbf{V}$ 都是正交矩阵，矩阵 $\mathbf{U}$ 的列向量被称为左奇异向量，矩阵 $\mathbf{V}$ 的列向量被称右奇异向量。
  • $\mathbf{D}$ 是对角矩阵（注意， $\mathbf{D}$ 不一定是方阵）。对角矩阵 $\mathbf{D}$ 对角线上的元素被称为矩阵 $\mathbf{A}$ 的奇异值。

AI中的应用：SVD 最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。而且大家在推荐系统中也会见到基于 SVD 的算法应用。

8.Moore-Penrose广义逆/伪逆（Moore-Penrose Pseudoinverse）

假设在下面问题中，我们想通过矩阵 $\mathbf{A}$ 的左逆 $\mathbf{B}$ 来求解线性方程： $\mathbf{A}x=y$ ，等式两边同时左乘左逆B后，得到： $x=\mathbf{B}y$ 。是否存在唯一的映射将 $\mathbf{A}$ 映射到 $\mathbf{B}$ ，取决于问题的形式：

• 如果矩阵 $\mathbf{A}$ 的行数大于列数，那么上述方程可能没有解；
• 如果矩阵 $\mathbf{A}$ 的行数小于列数，那么上述方程可能有多个解。

Moore-Penrose 伪逆使我们能够解决这种情况，矩阵 $\mathbf{A}$ 的伪逆定义为：

$${\mathbf{A}}^{+}=\underset{a\to 0}{\lim }{\left({\mathbf{A}}^T\mathbf{A}+\alpha \mathbf{I}\right)}^{-1}{\mathbf{A}}^T$$

但是计算伪逆的实际算法没有基于这个式子，而是使用下面的公式：

$${\mathbf{A}}^{+}=\mathbf{U}{\mathbf{D}}^{+}{\mathbf{V}}^T$$

• 矩阵 $\mathbf{U}$ 、 $\mathbf{D}$ 和 ${\mathbf{V}}^T$ 是矩阵 $\mathbf{A}$ 奇异值分解后得到的矩阵；
• 对角矩阵 $\mathbf{D}$ 的伪逆 ${\mathbf{D}}^{+}$ 是其非零元素取倒之后再转置得到的。

9.常用的距离度量

在机器学习里，大部分运算都是基于向量的，一份数据集包含n个特征字段，那每一条样本就可以表示为n维的向量，通过计算两个样本对应向量之间的距离值大小，有些场景下能反映出这两个样本的相似程度。还有一些算法，像 KNN 和 K-means，非常依赖距离度量。

设有两个 $n$ 维变量：

$$A=[x_{11},x_{12},...,x_{1n}{]}^T$$

$$B=[x_{21},x_{22},...,x_{2n}{]}^T$$

一些常用的距离公式定义如下：

1）曼哈顿距离（Manhattan Distance）

曼哈顿距离也称为城市街区距离，数学定义如下：

$$d_{12}=\sum _{k=1}^n|x_{1k}-x_{2k}|$$

曼哈顿距离的Python实现：

import numpy as np
vector1 = np.array([1,2,3])
vector2 = np.array([4,5,6])

manhaton_dist = np.sum(np.abs(vector1-vector2))
print("曼哈顿距离为", manhaton_dist)

前往我们的在线编程环境运行代码：http://blog.showmeai.tech/python3-compiler/#/

2）欧氏距离（Euclidean Distance）

欧氏距离其实就是L2范数，数学定义如下：

$$d_{12}=\sqrt{\sum _{k=1}^n(x_{1k}-x_{2k}{)}^2}$$

欧氏距离的Python实现：

import numpy as np
vector1 = np.array([1,2,3])
vector2 = np.array([4,5,6])

eud_dist = np.sqrt(np.sum((vector1-vector2)**2))
print("欧式距离为", eud_dist)

前往我们的在线编程环境运行代码：http://blog.showmeai.tech/python3-compiler/#/

3）闵氏距离（Minkowski Distance）

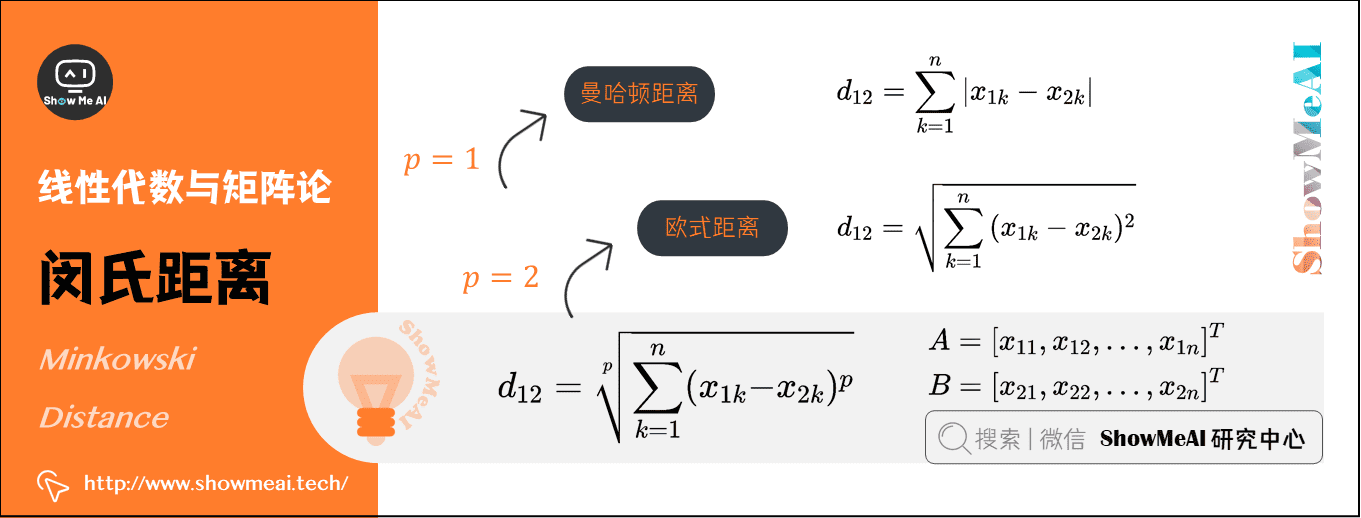
从严格意义上讲，闵可夫斯基距离不是一种距离，而是一组距离的定义：

$$d_{12}=\sqrt[p]{\sum _{k=1}^n(x_{1k}-x_{2k}{)}^p}$$

实际上，当 $p=1$ 时，就是曼哈顿距离；当 $p=2$ 时，就是欧式距离。

前往我们的在线编程环境运行代码：http://blog.showmeai.tech/python3-compiler/#/

4）切比雪夫距离（Chebyshev Distance）

切比雪夫距离就是无穷范数，数学表达式如下：

$$d_{12}=max(|x_{1k}-x_{2k}|)$$

切比雪夫距离的Python实现如下：

import numpy as np
vector1 = np.array([1,2,3])
vector2 = np.array([4,5,6])

cb_dist = np.max(np.abs(vector1-vector2))
print("切比雪夫距离为", cb_dist)

前往我们的在线编程环境运行代码：http://blog.showmeai.tech/python3-compiler/#/

5）余弦相似度（Cosine Similarity）

余弦相似度的取值范围为 $[-1,1]$ ，可以用来衡量两个向量方向的差异：

• 夹角余弦越大，表示两个向量的夹角越小；
• 当两个向量的方向重合时，夹角余弦取最大值 $1$ ；
• 当两个向量的方向完全相反时，夹角余弦取最小值 $-1$ 。

机器学习中用这一概念来衡量样本向量之间的差异，其数学表达式如下：

$$cos\theta =\frac{AB}{|A||B|}=\frac{{\sum }_{k=1}^n{x}_{1k}{x}_{2k}}{\sqrt{{\sum }_{k=1}^n{x}_{1k}^2}\sqrt{{\sum }_{k=1}^n{x}_{2k}^2}}$$

夹角余弦的Python实现：

import numpy as np
vector1 = np.array([1,2,3])
vector2 = np.array([4,5,6])

cos_sim = np.dot(vector1, vector2)/(np.linalg.norm(vector1)*np.linalg.norm(vector2))
print("余弦相似度为", cos_sim)

前往我们的在线编程环境运行代码：http://blog.showmeai.tech/python3-compiler/#/

6）汉明距离（Hamming Distance）

汉明距离定义的是两个字符串中不相同位数的数目。例如，字符串 1111 与 1001 之间的汉明距离为 $2$。信息编码中一般应使得编码间的汉明距离尽可能的小。

$$d_{12}=\sum _{k=1}^n\left(x_{1k}\oplus x_{2k}\right)$$

汉明距离的Python实现：

import numpy as np
a=np.array([1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0])
b=np.array([1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1])
hanm_dis = np.count_nonzero(a!=b)
print("汉明距离为", hanm_dis)

前往我们的在线编程环境运行代码：http://blog.showmeai.tech/python3-compiler/#/

7）杰卡德系数（Jaccard Index）

两个集合 $A$ 和 $B$ 的交集元素在 $A$ 和 $B$ 的并集中所占的比例称为两个集合的杰卡德系数，用符号 $J(A,B)$ 表示，数学表达式为：

$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}$$

杰卡德相似系数是衡量两个集合的相似度的一种指标。一般可以将其用在衡量样本的相似度上。

前往我们的在线编程环境运行代码：http://blog.showmeai.tech/python3-compiler/#/

8）杰卡德距离（Jaccard Distance）

与杰卡德系数相反的概念是杰卡德距离，其定义式为：

$$J_{\sigma }=1-J(A,B)=\frac{|A\cup B|-|A\cap B|}{|A\cup B|}$$

杰卡德距离的Python实现：

import numpy as np
vec1 = np.random.random(10)>0.5
vec2 = np.random.random(10)>0.5

vec1 = np.asarray(vec1, np.int32)
vec2 = np.asarray(vec2, np.int32)

up=np.double(np.bitwise_and((vec1 != vec2),np.bitwise_or(vec1 != 0, vec2 != 0)).sum())
down=np.double(np.bitwise_or(vec1 != 0, vec2 != 0).sum())
jaccard_dis =1-(up/down)
print("杰卡德距离为", jaccard_dis)

前往我们的在线编程环境运行代码：http://blog.showmeai.tech/python3-compiler/#/

ShowMeAI人工智能数学要点速查（完整版）

• ShowMeAI 图解AI数学基础(1) | 线性代数与矩阵论
• ShowMeAI 图解AI数学基础(2) | 概率与统计
• ShowMeAI 图解AI数学基础(3) | 信息论
• ShowMeAI 图解AI数学基础(4) | 微积分与最优化

ShowMeAI系列教程精选推荐

• 大厂技术实现：推荐与广告计算解决方案
• 大厂技术实现：计算机视觉解决方案
• 大厂技术实现：自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读