在机器学习领域,涉及到图论的地方会经常遇到 拉普拉斯矩阵(Laplacian Matrix)。在各类科普文、论文通常会直接给出拉普拉斯矩阵的定义:
L=D−W
其中, D 为图的度矩阵(Degree Matrix),度矩阵是一个对角矩阵(Diagonal Matrix),其对角线元素等于该节点在图中的度, W 为邻接矩阵(Adjacency Matrix)。
但是,为什么矩阵 L 被称作拉普拉斯矩阵?为什么矩阵 L 是这样一个形式?拉普拉斯矩阵究竟包含了图的什么信息?为什么涉及到图论的相关算法会经常使用拉普拉斯矩阵?它有什么性质?
为了彻底的理解拉普拉斯矩阵,我们首先从拉普拉斯算子(Laplace operator)谈起。
拉普拉斯算子
拉普拉斯算子 Δf 是 n 维欧几里德空间中的一个二阶微分算子,定义为函数 f 梯度(∇f )的散度( ∇⋅∇f ), 即
Δf=∇2f=∇⋅∇f
这里涉及到两个基本数学概念,梯度与散度(Divergence)。
梯度(Gradient)
梯度是一个向量(矢量),设有一个二元函数 z=f(x,y) 具有一阶连续偏导数,则其在点 (x,y) 处的梯度为:
∇f(x,y)=∂f∂x⋅i→+∂f∂y⋅j→
∇ 又叫做nabla算子,其作用于一个 标量函数 f(x,y) ,得到一个 矢量函数 ∇f(x,y) ,即梯度是一个矢量函数。
梯度矢量 ∇f(x,y) 的几何意义在于,在点 (x,y) 处,沿着该矢量的方向(也就是梯度的方向),函数值 f(x,y) 的增长最快,也就是变化率最大(变化率为该矢量的模)。

为了理解的方便,我们可以把 f(x,y)所构成的三维曲面想象为一个二维平面上的曲线,如上图所示,并把该曲线想象成一个山脊。那么,对于山顶 M 附近的点 (x0,y0) 与 (x1,y1) ,其梯度矢量如绿色箭头所示,指向函数值增大的方向,即山顶的方向。对于山谷 N 附近的点 (x2,y2) 与 (x3,y3) ,其梯度矢量如绿色箭头所示,也指向函数值增大的方向,即背离山谷指向山顶的方向。
散度(Divergence)
散度是一个标量,设有一个向量场 F(x,y)=P(x,y)⋅i→+Q(x,y)⋅j→,其散度为
∇⋅F=[∂∂xi→+∂∂yj→]⋅[Pi→+Qj→]=∂P∂x+∂Q∂y
相互正交的单位矢量内积为0,而同方向的单位矢量内积为1,所以,最后得到的散度是一个标量,即散度是一个标量函数,是由一个矢量函数得到的。这与前面提到的梯度相反。这里散度是在直角坐标系下定义的,其几何意义并不明显。
拉普拉斯算子(Laplace operator)
回到拉普拉斯算子 Δf 的定义——拉普拉斯算子是函数 f 梯度(∇f)的散度( ∇⋅∇f )。为了理解拉普拉斯算子的实际意义,我们回到上图的山脊线,在山脊线中,我们可以计算得到每一点的梯度,这些梯度就可以构成梯度场,即矢量函数∇f。

俗话说,人往高处走,水往低处流。在这条山脊线上,任何一个地方的人都向山顶走,为了能更快地到达山顶,走的方向即为梯度的方向(函数值增加最快的方向)。假设我们在这条山脊线上均匀地放置100个人,那么过了一段时间后,山顶的人越来越多,山谷的人就会越来越少。对于山顶 M ,我们想用一个标量来直观表示人越来越多这种情况,相应的,对于山谷 N ,也想用一个标量来表示人越来越少这种情况。但是,现在只有矢量函数∇f ,如何得到这样标量呢?
用一个很简单的办法,我们在山谷附近画一个圈,如果这个圈上某个点的梯度方向指向圈外,就说明当人到达这个点时候,他要离开这个圈;如果指向圈内,说明他将进入这个圈。我们可以试着作出圈上这一点的法向量,如上图橙色箭头所示,将这个法向量与梯度向量进行点乘,我们可以发现:当梯度方向指向圈外的时候,点乘后的数值为正(两向量的夹角小于90°, cos(θ)>0 );当梯度方向指向圈内的时候,点乘后的数值为负(两向量的夹角大于90°, cos(θ)<0 ),并且数值大小反映了离开或者进入圈的迫切程度。这正是我们要寻找的标量!
我们将这个圈不断的缩小,缩到足够小,只包含 M 点或者 N 点,这时候可以预料,M 点的标量值为负, N 点的标量值为正。实际上,M点的这个标量值,即为拉普拉斯算子在 M 点的数值。以上推导过程,实际用到了散度的另一种定义:

其中, |V| 即为这个圈的体积, S(V) 为这个圈的边界, n^ 为与圈边界上指向外的单位向量。
所以,从以上分析可看出,散度表示了向量场的发散程度,散度为正,值越大,向量场在处发散地越强烈;而散度为负,值越小,向量场在处汇集地越强烈。而拉普拉斯算子实际上衡量的正是梯度场的发散程度。也即是上面的例子中,对人的吸引或者排斥程度。
我们回到直角坐标系下的散度定义,令 F(x,y)=∇f(x,y) ,则拉普拉斯算子为

这里我们简化,以二维图像为例,如下图所示

考虑像素点 (x,y) 的拉普拉斯算子:

从这个角度讲,就是对二维图像的像素点 (x,y) ,沿着可能变化的四条路径,分别移动一步,所获得的增益,这个增益实际上就是前面提到的对人的吸引程度,或者说是人口净流入。我们继续画一个圈,假设 f(x+1,y) 大于 f(x,y) ,即沿着 x 轴正方向这条边,山变高,人希望往高处走,那么就有人会沿着这条边走出这个圈。如果f(x,y+1) 小于 f(x,y),说明 在(x,y+1) 处的山低于 (x,y) ,人往高处走,就会进入这个圈。把四条边综合起来,就是圈内的人口净流出,由于圈内只有一个点 (x,y) ,即为点 (x,y) 的人口净流出或者是吸引程度。
拉普拉斯矩阵
拉普拉斯矩阵是定义在图上的,看到这里,聪明的你肯定已经想到,上面二维图像的例子不就是一个包含5个节点的图嘛!我们计算的是中心点 (x,y) 的拉普拉斯算子,其余四个点在该点的邻域内,四条路径即为该点的四条边。我们将这个计算过程推广到整个图上:

设图 G 具有 n 个节点,节点 i 的邻域为 Ni ,在图上定义一个函数 f=(f1,f2,...,fn) ,其中 fi 表示函数 f 在节点 i 处的函数值。让节点i沿着各条边,向邻域内的所有节点 j∈Ni 移动,计算所有的增益

如果考虑每一条边的权重wij, wij=0 表示节点 i 与节点 j 不相邻,那么增益变为:

其中 di为节点 i 的度,wi:=(wi1,…,wiN) 是 N维的行向量f是 N维的列向量。
对于整个图G,有

这里,拉普拉斯矩阵的每 i 行,第 j 列的元素实际代表,从节点 j 到节点 i 所获得的增益值(注意这里考虑了上面的负号, W−D 代表的是 (fj−fi) ,加上负号就是 (fi−fj) ,得到的就是拉普拉斯矩阵)与节点 j 的值之间的比例系数。我们可以把 N 个节点想象为N座山峰,fi为山峰 i 的海拔高度,两个节点之间边则代表两座山峰之间有路径,拉普拉斯矩阵实际就是嵌入了某一个山峰对在其他山峰上的人的吸引程度,或者说是一种人口流动倾向。
拉普拉斯矩阵的性质
拉普拉斯矩阵是一个半正定对称矩阵,即有 LT=L ,若对于任意长度为n的向量x,有xTLx≥0恒成立,并且拉普拉斯矩阵的 n 个特征值 λ1,λ2,...,λn 都是非负值,即 0=λ1≤λ2≤...≤λn。
这里引入瑞丽熵 R(A,x) 的定义:
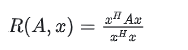
其中, x 是非零向量,而 A 为 n×n 的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵,即 AH=A ,且当 A 为实矩阵时,即 AT=A 。
利用拉格朗日乘子法,可以得到瑞利商 R(A,x) 的一个非常重要的性质:瑞利熵的最大值等于矩阵 A 最大的特征值,而最小值等于矩阵 A 的最小的特征值,也就是满足

当向量 x 为标准正交基,即满足 xHx=1 时,瑞利商退化为 R(A,x)=xHAx 。
所以在拉普拉斯矩阵的相关运算中,经常出现 fTLf ,例如谱聚类等算法即是利用了这一特点。























 1231
1231

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








