分类问题
分类问题回答某个样本从属于哪个分类的问题。 分为二分分类和多类分类。
二分分类回答,一个样本是否从属于某个分类的问题。而多类分类则要在多个分类中找到一个它丛书的分类。
回归问题
实际上,分类问题是使用回归为基础来实现的。 回归问题可以简要的描述为以下形式
对于给定的数据集
D={(x0,y0),(x1,y1),...,(xk,yk)}
寻找一个函数
f
使得
f(x)=wx+b
的形式。 ,然后估测w和b。
那么如何描述上面说的” f(x) 的值尽可能的接近原本的y的值” ,可以这么描述
即以w和b作为参数时, 估计值和真实值的差的平方的和。
最小二乘法
将上述公式求导并令导数为0,就得到了最小二乘法。
令偏导数为0,可以求得w和b。这就是最小二乘法。
梯度下降法
能直接解出最优解多么快捷方便? 那么一般问题为什么不能使用最小二乘法呢? 因为最小二乘法只能解决线性问题,对于一些非线性的函数,是难以通过公式推到而求解的。这个时候就用到了梯度下降法。
参考下图,我们从任意一点开始,如何才能最快达到最大点?那就是沿着下降最快的方向走可以很快的到达低点。每次都沿下降最快的方向走一步,一直到走不动(在一个谷底),算法结束。
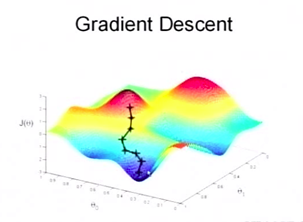

当然,有可能会达到一个极值点,而非最值点。如图
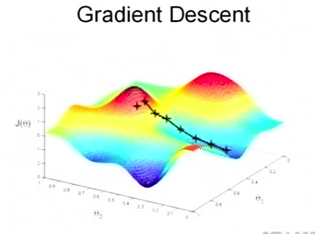

那么应当如何找到下降最快的方向呢? 我们看一个最简单的例子。

一个x为一维时的图。 当x从小变大时,f(x)增加,导数为正,f(x)减少,导数为负数。
那么当导数为正时,我们在爬坡,要想让函数值尽量减小那么就应该向x减少的方向走。
当导数为负数时,我们在下坡,那么为了减小函数值,我们就应当往前走。
为什么是这样的? 看导数的定义就知道了

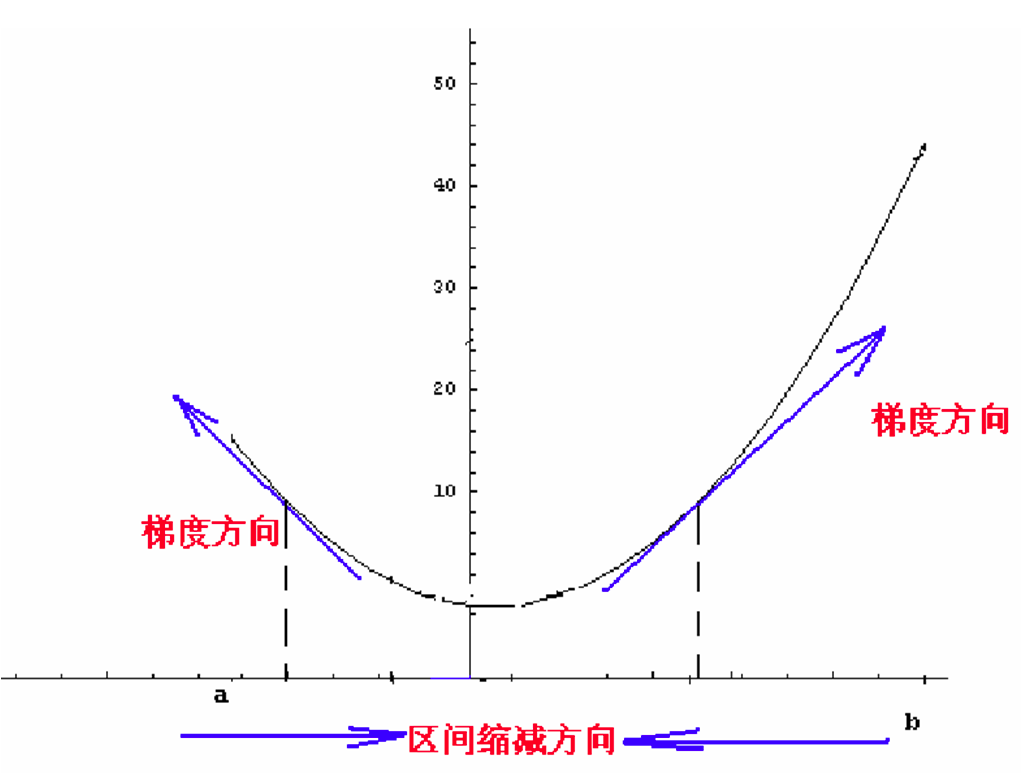
按照上述分析,我们应该向导数(梯度)的反方向走,所以。我们:
讲本节最上面的公式带入
Logistic回归
上面都是线性回归,适用于函数是一个连续值的情况,对于一个二分问题。
这是一个很不连续的函数
如果使用 y=wx+b 这样的公式来进行拟合,那么可能出现>1 和<0的情况。如果我们向用y表示x从属于某类的概率,>1和<0的情况显然不合法。那么有没有函数值处于0和1之间的函数呢? 有!!!!!就是Logistic函数

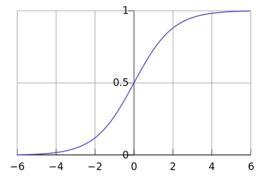
他的自变量取值为负无穷到正无穷。函数值是0-1太完美了。同时他是一个增函数。正好可以表示概率。
【我估计发明者就是凑出来的】
损失函数
为什么要定义损失函数
那么我们如何评价一个算法分类的好坏的? 通俗的讲 分类正确的越多越好,那么怎么用数学描述这个说法呢?
我们给出了损失函数。 使得 当分类错误的越多, 损失函数越大。
我们在进行学习的时候,想办法通过迭代的方法让损失函数不断减小,知道我们能达到的最小损失。这样得到的结果就是比较优良的。
0-1 损失函数(Zero-One Loss)
最直观的定义,就是统计分类错误的样本个数,如下:
我们假设有L个类
{0,...,L}
,使用
D
来表示数据集。分类问题可以看做是一种映射:
f:RD→{0,...,L}
,则损失函数可定义为:
其中
f(x(i))
表示第i个样本会被分到哪一个类中,他的返回值是一个类的序号,也就是通过函数f,得到一个分类结果。
yi
表示第i个样本的真实分类。 如
果不想等,则
Ix=1
。
Ix
的定义如下:
使用以上定义,我们就可以表示出”有多少样本分错了类”这个问题。
使用theano,上述公式可以描述为:
zero_one_loss = T.sum(T.neq(ye, y))ye表示估计值,y是真实值。程序的表示似乎比数学简明多了。
负对数似然损失 (Negative Log-Likelihood Loss,NLL)
我们求解一个优化问题,有一个简单的思路,就是求出损失函数的导数,当他的导数等于0时,他就达到了极值。那么就需要对损失函数求导,非常遗憾的是,上面的0-1损失函数是一个离散的函数,不能求导(不可微)。
那么人民就提出了一个连续的损失函数。
因为我们的Logistic函数是一个从0-1的函数,可以看成是概率。即
那么我们可以用概率的方法来定义损失函数。
概率中有一种非常常用的方法叫做 最大似然估计。对于已知样本
我们试图估计一个参数,使得当x取值 x(0),x(1),...,x(k) 时,y的估计值 的概率最大。
最大似然为:
那么对数最大似然就是对他进行求对数得到:
损失函数越小代表模型越好即
θ
的取值约正确。 相反的,最大似然越大,说明模型越好,
θ
越正确。所以我们给最大似然加一个负号来表示损失函数。
梯度下降与随机梯度下降
使用梯度下降使损失函数最小。对于上述的损失函数,每次迭代都要计算所有的样本。如果样本数量有几十万,那么速度会相当的慢,将损失函数稍作改写:
求损失函数的粒度为每个样本。这样我们就可以改写迭代函数为

1. 批量梯度下降—最小化所有训练样本的损失函数,使得最终求解的是全局的最优解,即求解的参数是使得风险函数最小。
- 随机梯度下降—最小化每条样本的损失函数,虽然不是每次迭代得到的损失函数都向着全局最优方向, 但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近。
softmax回归
当我们处理二分问题时
y(i)∈{0,1}
,我们使用
我们将训练模型参数 \textstyle \theta,使其能够最小化代价函数 :
对于一个多类分类问题。 {(x(1),y(1)),…,(x(m),y(m))} , y(i)∈{1,2,…,k} 。
使用上述函数为x从属于每个类都计算一个概率。 最后选择值最大的那个类做为最终估计的结果。






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








