以后轴中心为原点的车辆运动学模型及其线性化
车辆的运动学模型有好几种,以质心为原点、前轴中心为原点、后轴中心为原点。单独把以后轴中心为原点的模型拎出来讲是因为这个模型在做轨迹跟踪时比较好线性化,像其它两种模型里有三角关系的嵌套耦合,线性化的时候实在太麻烦了,不利于控制。而且在好几个地方都看到过这个模型,包括apollo里轨迹拼接时预测未来状态用的也是以后轴中心为原点的模型。
车辆运动学模型
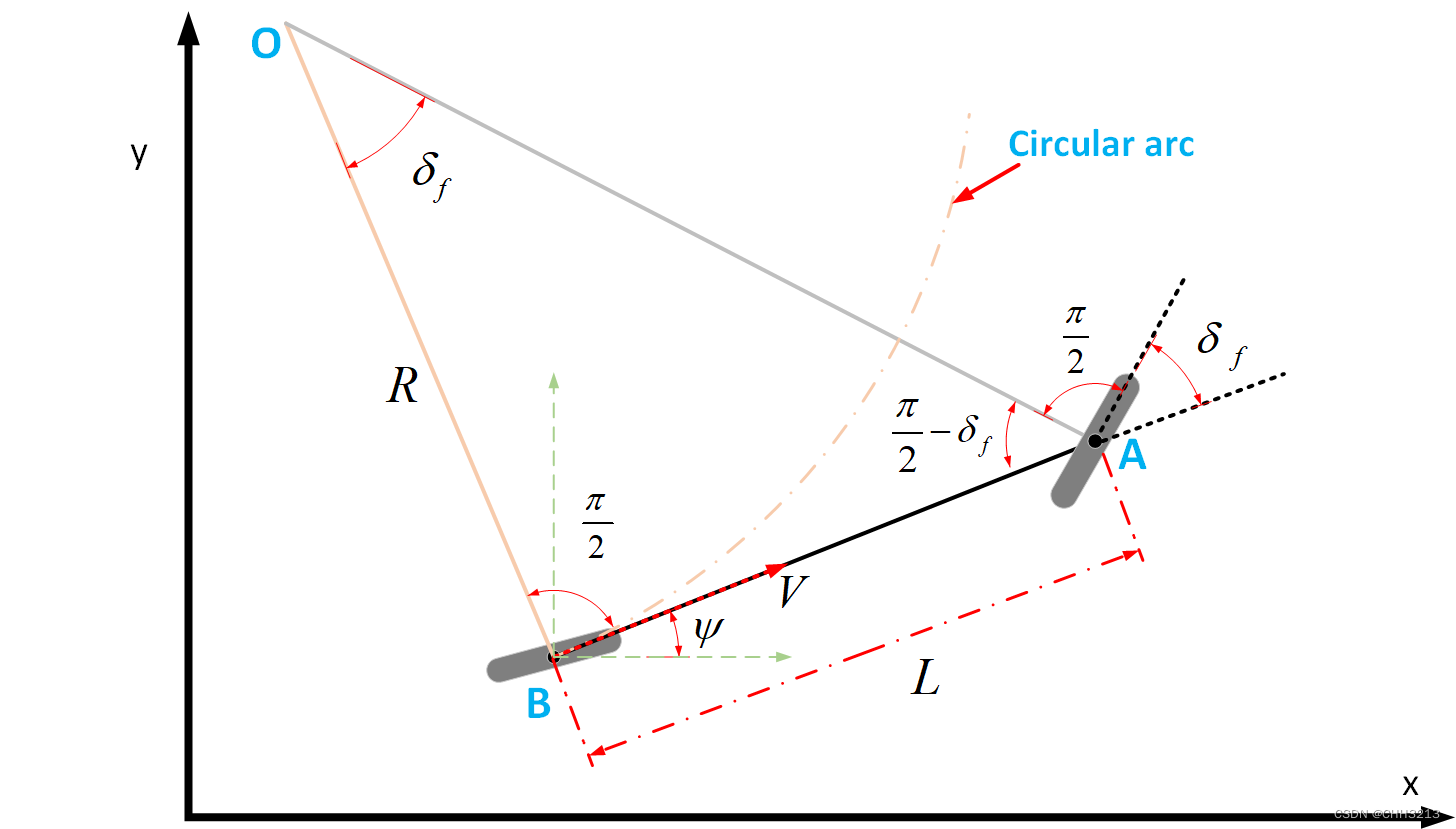
{ x ˙ = v cos ( ψ ) = f 1 y ˙ = v sin ( ψ ) = f 2 ψ ˙ = v L tan ( δ f ) = f 3 \left\{ \begin{aligned} &\dot{x} = v\cos(\psi) = f_1\\ &\dot{y} = v\sin(\psi) = f_2\\ &\dot{\psi} = \frac{v}{L}\tan(\delta_f) = f_3 \end{aligned} \right. ⎩ ⎨ ⎧x˙=vcos(ψ)=f1y˙=vsin(ψ)=f2ψ˙=Lvtan(δf)=f3
这个模型的具体推导过程同样也是应用两次正弦定理,思路可以参考这篇博客。
泰勒展开公式
f
(
x
)
=
f
(
x
0
)
0
!
+
f
′
(
x
0
)
1
!
(
x
−
x
0
)
+
f
′
′
(
x
0
)
2
!
(
x
−
x
0
)
2
+
.
.
.
+
f
(
n
)
(
x
0
)
n
!
(
x
−
x
0
)
n
+
R
n
(
x
)
f(x) = \frac{f(x_0)}{0!} + \frac{f{'}(x_0)}{1!}(x - x_0) + \frac{f^{''}(x_0)}{2!}(x - x_0)^2 + ... + \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n + R_n(x)
f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...+n!f(n)(x0)(x−x0)n+Rn(x)
其中
f
(
n
)
(
x
)
f^{(n)}(x)
f(n)(x)表示
f
(
x
)
f(x)
f(x)的
n
n
n阶导,等号后的多项式表示函数
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0处的泰勒展开式,
R
n
(
x
)
R_n(x)
Rn(x)是高阶的余项,是
(
x
−
x
0
)
n
(x - x_0)^{n}
(x−x0)n的高阶无穷小。
模型线性化
设系统状态 X = [ x , y , ψ ] T X=[x, y, \psi]^T X=[x,y,ψ]T,系统输入 u = [ v , δ f ] T u=[v, \delta_f]^T u=[v,δf]T。把模型线性化就是找到一组线性关系 A , B A, B A,B,使得 X ˙ = A X + B u \dot{X} = AX + Bu X˙=AX+Bu。
对于上面的单车模型来说,变换关系为 X ˙ = f ( X , u ) \dot{X} = f(X, u) X˙=f(X,u), f = [ f 1 , f 2 , f 3 ] T f = [f_1, f_2, f_3]^T f=[f1,f2,f3]T为一个非线性的函数,因此需要采用线性化。
对需要跟踪的参考轨迹上的一个点
(
X
r
,
u
r
)
(X_r, u_r)
(Xr,ur),
X
r
X_r
Xr表示参考状态,
u
r
u_r
ur表示参考输入,进行泰勒展开并忽略高阶项:
X
˙
=
f
(
X
r
,
u
r
)
+
∂
f
(
X
r
,
u
r
)
∂
X
(
X
−
X
r
)
+
∂
f
(
X
r
,
u
r
)
∂
u
(
u
−
u
r
)
\dot{X} = f(X_r, u_r) + \frac{\partial f(X_r, u_r)}{\partial X}(X - X_r) + \frac{\partial f(X_r, u_r)}{\partial u}(u - u_r)
X˙=f(Xr,ur)+∂X∂f(Xr,ur)(X−Xr)+∂u∂f(Xr,ur)(u−ur)
∂ f ( X , u ) ∂ X = [ f 1 ∂ x f 1 ∂ y f 1 ∂ ψ f 2 ∂ x f 2 ∂ y f 2 ∂ ψ f 3 ∂ x f 3 ∂ y f 3 ∂ ψ ] = [ 0 0 − v sin ( ψ ) 0 0 v cos ( ψ ) 0 0 0 ] \frac{\partial f(X, u)}{\partial X} = \begin{bmatrix} \frac{f_1}{\partial x} & \frac{f_1}{\partial y} & \frac{f_1}{\partial \psi} \\ \frac{f_2}{\partial x} & \frac{f_2}{\partial y} & \frac{f_2}{\partial \psi} \\ \frac{f_3}{\partial x} & \frac{f_3}{\partial y} & \frac{f_3}{\partial \psi} \end{bmatrix} = \begin{bmatrix} 0 & 0 & -v\sin(\psi) \\ 0 & 0 & v\cos(\psi) \\ 0 & 0 & 0 \end{bmatrix} ∂X∂f(X,u)= ∂xf1∂xf2∂xf3∂yf1∂yf2∂yf3∂ψf1∂ψf2∂ψf3 = 000000−vsin(ψ)vcos(ψ)0
∂
f
(
X
,
u
)
∂
u
=
[
f
1
∂
v
f
1
∂
δ
f
2
∂
v
f
2
∂
δ
f
3
∂
v
f
3
∂
δ
]
=
[
cos
(
ψ
)
0
sin
(
ψ
)
0
tan
(
δ
)
L
v
L
cos
2
(
δ
f
)
]
\frac{\partial f(X, u)}{\partial u} = \begin{bmatrix} \frac{f_1}{\partial v} & \frac{f_1}{\partial \delta} \\ \frac{f_2}{\partial v} & \frac{f_2}{\partial \delta} \\ \frac{f_3}{\partial v} & \frac{f_3}{\partial \delta} \end{bmatrix} = \begin{bmatrix} \cos(\psi) & 0 \\ \sin(\psi) & 0 \\ \frac{\tan(\delta)}{L} & \frac{v}{L\cos^2(\delta_f)} \end{bmatrix}
∂u∂f(X,u)=
∂vf1∂vf2∂vf3∂δf1∂δf2∂δf3
=
cos(ψ)sin(ψ)Ltan(δ)00Lcos2(δf)v
上面求雅各比矩阵可以参考这篇博客中的矩阵求导。
把这下面这两个关系代入到一阶泰勒展开式子中然后把
X
˙
r
\dot{X}_r
X˙r移到右边。
{
X
˙
=
f
(
X
,
u
)
X
r
˙
=
f
(
X
r
,
u
r
)
\left\{ \begin{aligned} & \dot{X} = f(X, u) \\ & \dot{X_r} = f(X_r, u_r) \end{aligned} \right.
{X˙=f(X,u)Xr˙=f(Xr,ur)
可以建立起轨迹跟踪的线性误差系统,本篇博客的结果就是下式,最终我们的控制目标就是让这个误差系统状态趋于0。
e
˙
X
=
X
˙
−
X
˙
r
=
[
0
0
−
v
r
sin
(
ψ
r
)
0
0
v
r
cos
(
ψ
r
)
0
0
0
]
e
X
+
[
cos
(
ψ
r
)
0
sin
(
ψ
r
)
0
tan
(
δ
f
r
)
L
v
r
L
cos
2
(
δ
f
r
)
]
e
u
=
A
e
x
+
B
e
u
\dot{e}_X = \dot{X} - \dot{X}_r = \begin{bmatrix} 0 & 0 & -v_r\sin(\psi_r) \\ 0 & 0 & v_r\cos(\psi_r) \\ 0 & 0 & 0 \end{bmatrix} e_X + \begin{bmatrix} \cos(\psi_r) & 0 \\ \sin(\psi_r) & 0 \\ \frac{\tan(\delta_{fr})}{L} & \frac{v_r}{L\cos^2(\delta_{fr})} \end{bmatrix} e_u = Ae_x + Be_u
e˙X=X˙−X˙r=
000000−vrsin(ψr)vrcos(ψr)0
eX+
cos(ψr)sin(ψr)Ltan(δfr)00Lcos2(δfr)vr
eu=Aex+Beu
所求的线性关系为:
A
=
[
0
0
−
v
r
sin
(
ψ
r
)
0
0
v
r
cos
(
ψ
r
)
0
0
0
]
,
B
=
[
cos
(
ψ
r
)
0
sin
(
ψ
r
)
0
tan
(
δ
f
r
)
L
v
r
L
cos
2
(
δ
f
r
)
]
A = \begin{bmatrix} 0 & 0 & -v_r\sin(\psi_r) \\ 0 & 0 & v_r\cos(\psi_r) \\ 0 & 0 & 0 \end{bmatrix}, B = \begin{bmatrix} \cos(\psi_r) & 0 \\ \sin(\psi_r) & 0 \\ \frac{\tan(\delta_{fr})}{L} & \frac{v_r}{L\cos^2(\delta_{fr})} \end{bmatrix}
A=
000000−vrsin(ψr)vrcos(ψr)0
,B=
cos(ψr)sin(ψr)Ltan(δfr)00Lcos2(δfr)vr
其中 u r = [ v r , δ f r ] T u_r = [v_r, \delta_{fr}]^T ur=[vr,δfr]T表示参考输入,在实际使用过程中,参考速度 v r v_r vr可以用固定值,参考前轮转向角 δ f r \delta_{fr} δfr可以用图1推导得 δ f r = arctan ( L R ) \delta_{fr} = \arctan(\frac{L}{R}) δfr=arctan(RL), R = 1 κ R=\frac{1}{\kappa} R=κ1表示转弯半径,曲率的倒数。
python实现
实现效果
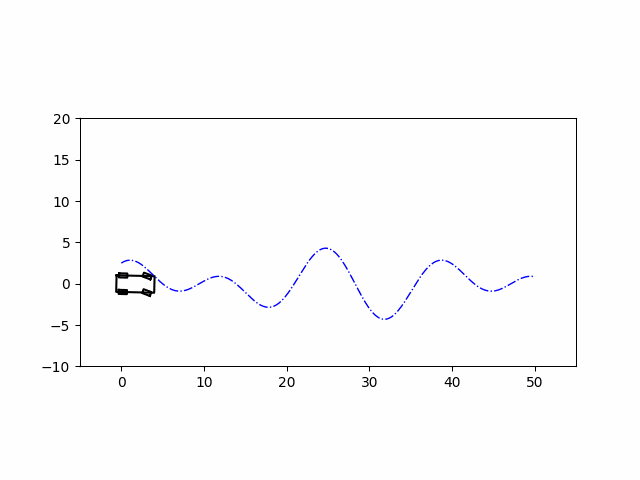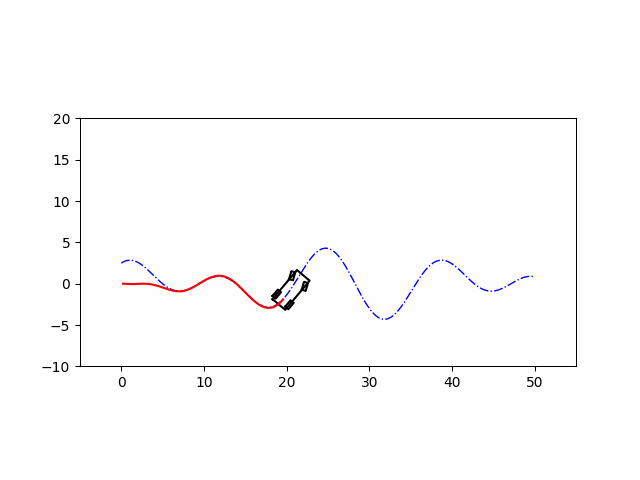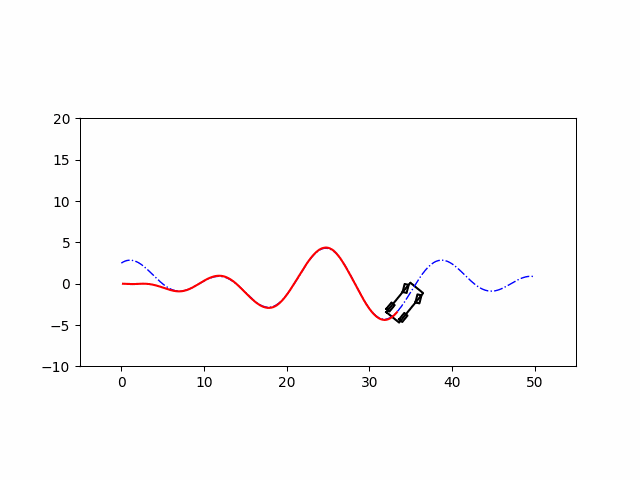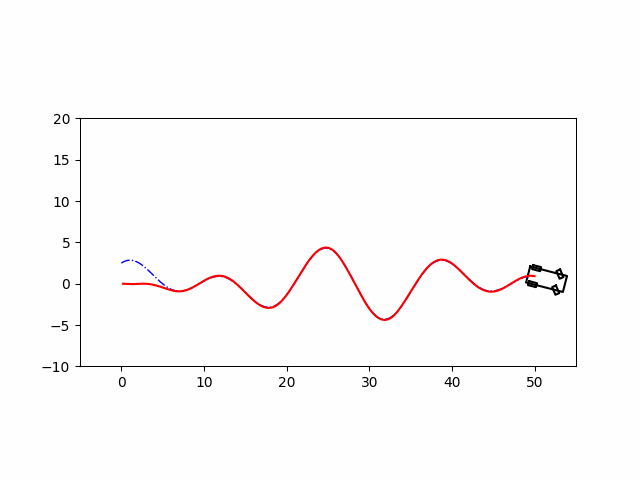
代码
import numpy as np
import math
class VehicleBaseModel:
def __init__(self, L = 2.9, width = 2.0, LF = 3.8, LB = 0.8, TR = 0.5, TW = 0.5, Iz = 2250.0, Cf = 1600.0 * 1.0, Cr = 1700.0 * 1.0, m = 1500.0, MWA = 30.0):
# 车辆参数信息
self.L = L # 轴距[m]
self.Lf = self.L / 2.0 # 车辆中心点到前轴的距离[m]
self.Lr = self.L - self.Lf # 车辆终点到后轴的距离[m]
self.width = width # 宽度[m]
self.LF = LF # 后轴中心到车头距离[m]
self.LB = LB # 后轴中心到车尾距离[m]
self.TR = TR # 轮子半径[m]
self.TW = TW # 轮子宽度[m]
self.WD = self.width # 轮距[m]
self.Iz = Iz # 车辆绕z轴的转动惯量[kg/m2]
self.Cf = Cf # 前轮侧偏刚度[N/rad]
self.Cr = Cr # 后轮侧偏刚度[N/rad]
self.m = m # 车身质量[kg]
self.len = self.LB + self.LF # 车辆长度[m]
self.MWA = np.radians(MWA) # 最大轮转角(Max Wheel Angle)[rad]
self.x_cartesian = 0.0 # 车辆笛卡尔坐标系x坐标
self.y_cartesian = 0.0 # 车辆笛卡尔坐标系y坐标
self.psi = 0.0 # 航向角
self.delta = 0.0 # 前轮转向角
self.dt = 0.01 # 离散时间
def normalize_angle(self, angle):
a = math.fmod(angle + np.pi, 2 * np.pi)
if a < 0.0:
a += (2.0 * np.pi)
return a - np.pi
def draw_vehicle(self, axis, color='black'):
vehicle_outline = np.array(
[[-self.LB, self.LF, self.LF, -self.LB, -self.LB],
[self.width / 2, self.width / 2, -self.width / 2, -self.width / 2, self.width / 2]])
wheel = np.array([[-self.TR, self.TR, self.TR, -self.TR, -self.TR],
[self.TW / 2, self.TW / 2, -self.TW / 2, -self.TW / 2, self.TW / 2]])
rr_wheel = wheel.copy() # 右后轮
rl_wheel = wheel.copy() # 左后轮
fr_wheel = wheel.copy() # 右前轮
fl_wheel = wheel.copy() # 左前轮
rr_wheel[1, :] += self.WD/2
rl_wheel[1, :] -= self.WD/2
# 方向盘旋转
rot1 = np.array([[np.cos(self.delta), -np.sin(self.delta)],
[np.sin(self.delta), np.cos(self.delta)]])
# psi旋转矩阵
rot2 = np.array([[np.cos(self.psi), -np.sin(self.psi)],
[np.sin(self.psi), np.cos(self.psi)]])
fr_wheel = np.dot(rot1, fr_wheel)
fl_wheel = np.dot(rot1, fl_wheel)
fr_wheel += np.array([[self.L], [-self.WD / 2]])
fl_wheel += np.array([[self.L], [self.WD / 2]])
fr_wheel = np.dot(rot2, fr_wheel)
fr_wheel[0, :] += self.x_cartesian
fr_wheel[1, :] += self.y_cartesian
fl_wheel = np.dot(rot2, fl_wheel)
fl_wheel[0, :] += self.x_cartesian
fl_wheel[1, :] += self.y_cartesian
rr_wheel = np.dot(rot2, rr_wheel)
rr_wheel[0, :] += self.x_cartesian
rr_wheel[1, :] += self.y_cartesian
rl_wheel = np.dot(rot2, rl_wheel)
rl_wheel[0, :] += self.x_cartesian
rl_wheel[1, :] += self.y_cartesian
vehicle_outline = np.dot(rot2, vehicle_outline)
vehicle_outline[0, :] += self.x_cartesian
vehicle_outline[1, :] += self.y_cartesian
axis.plot(fr_wheel[0, :], fr_wheel[1, :], color)
axis.plot(rr_wheel[0, :], rr_wheel[1, :], color)
axis.plot(fl_wheel[0, :], fl_wheel[1, :], color)
axis.plot(rl_wheel[0, :], rl_wheel[1, :], color)
axis.plot(vehicle_outline[0, :], vehicle_outline[1, :], color)
# ax.axis('equal')
# 补充说明:非线性不那么强,可以用泰勒展开进行线性化并控制
class KinematicModel_Rear(VehicleBaseModel):
def __init__(self, x = 0.0, y = 0.0, psi = 0.0, v = 0.0, dt = 0.01):
super().__init__()
self.x_cartesian = x
self.y_cartesian = y
self.psi = psi
self.v = v
self.dt = dt
self.nx = 3
self.nu = 2
self.state_X = np.matrix([[self.x_cartesian], [self.y_cartesian], [self.psi]])
# 真实模型和数学模型的状态更新
def model_update(self, u):
# 车辆真实模型的状态更新
#self.v = u[0, 0]
#self.delta = np.clip(u[1, 0], -self.MWA, self.MWA)
self.delta = u[1, 0]
x_dot = self.v * math.cos(self.psi)
y_dot = self.v * math.sin(self.psi)
psi_dot = self.v / self.L * math.tan(self.delta)
self.x_cartesian = self.x_cartesian + x_dot * self.dt
self.y_cartesian = self.y_cartesian + y_dot * self.dt
self.psi = self.psi + psi_dot * self.dt
self.psi = self.normalize_angle(self.psi)
self.state_X = np.mat([[self.x_cartesian], [self.y_cartesian], [self.psi]])
def state_space_model(self, delta_ref, psi_ref):
A = np.mat([
[0.0, 0.0, -self.v * math.sin(psi_ref)],
[0.0, 0.0, self.v * math.cos(psi_ref)],
[0.0, 0.0, 0.0]])
B = np.mat([
[math.cos(psi_ref), 0],
[math.sin(psi_ref), 0],
[math.tan(delta_ref) / self.L, self.v / (self.L * math.cos(delta_ref) * math.cos(delta_ref))]
])
return A, B





















 597
597

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








