卡尔曼滤波
数据融合例子
卡尔曼滤波是一个数据融合的过程,先验数据和后验数据融合,即找到一个合适的权重,取两个数据的加权和。
举一个简单的例子直观理解(来源):用两个秤去称同一个物体,得到同一个物体的两个重量和标准差(符合正态分布)为:
z
1
=
30
g
σ
1
=
2
g
z
2
=
32
g
σ
2
=
4
g
z_1 = 30g \quad \sigma_1 = 2g\\ z_2 = 32g \quad \sigma_2 = 4g
z1=30gσ1=2gz2=32gσ2=4g
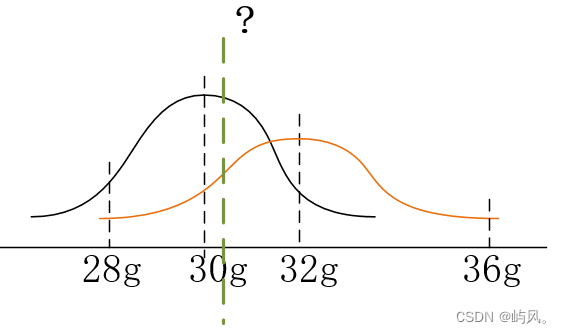
如上图所示,但是这两个值都是量测值,都是用秤称出来的,都存在误差,并不是物体的真实重量。问题就在于怎么找到物体的真实的重量值,图中绿色线表示的值。凭感觉应该在30-32之间,但具体是多少呢。就需要对这两个量测值进行加权求和:
z
^
=
z
1
+
k
(
z
2
−
z
1
)
\hat{z} = z_1 + k(z_2 - z_1)
z^=z1+k(z2−z1)
式中,
z
^
\hat{z}
z^表示对物体真实重量值的估计值,由
z
1
z_1
z1和
z
2
z_2
z2加权而来;
k
k
k表示加权权重,
k
=
0
k=0
k=0时表示完全相信量测值
z
1
z_1
z1,
k
=
1
k=1
k=1时表示完全相信量测值
z
2
z_2
z2。一般来说是取一个中间值,卡尔曼滤波的目的就是确定这个中间值,使估计值
z
^
\hat{z}
z^尽可能接近真值。其思想很简单,假如第一个秤误差小一点,那么更偏向于相信
z
1
z_1
z1,
k
k
k值小一点;假如第二个秤误差小一点,那么更偏向于相信
z
2
z_2
z2,
k
k
k值大一点。这里就需要引入协方差阵来量化地描述每个秤的误差大小。
卡尔曼滤波的思想
根据马斯克常讲的第一性原理,做一个事之前要知道它到底是做什么的。对于这里的卡尔曼滤波来讲,就是确定 z ^ = z 1 + k ( z 2 − z 1 ) \hat{z} = z_1 + k(z_2 - z_1) z^=z1+k(z2−z1)这式子中的加权权重 k k k是多少,能够通过有限的量测和预测让估计值 z ^ \hat{z} z^尽可能接近真值。那么核心思想就是如何找最优权重以及如何定义最优。
找最优权重
x
^
k
=
x
^
k
−
+
G
(
H
−
1
z
k
−
x
^
k
−
)
\hat{x}_k = \hat{x}_k^- + G(H^{-1}z_k - \hat{x}_k^-)
x^k=x^k−+G(H−1zk−x^k−)
可以令
G
=
K
k
H
G=K_kH
G=KkH(这样就避免了矩阵求逆,总能找到一个
K
k
K_k
Kk,使这个式子成立),那么上面的公式就变成了:
x
^
k
=
x
^
k
−
+
K
k
(
z
k
−
H
x
^
k
−
)
(1)
\hat{x}_k = \hat{x}_k^- + K_k(z_k - H\hat{x}_k^-) \tag{1}
x^k=x^k−+Kk(zk−Hx^k−)(1)
这里的
K
k
K_k
Kk就是要找的最优权重,给预测值和量测值不同的权重,使得估计值
x
^
k
\hat{x}_k
x^k最优。
如何定义最优
卡尔曼滤波中最优的定义,是让真值与估计值误差的方差之和最小,这样就能让估计值尽量的平滑,实现滤波。方差之和即是协方差矩阵的对角线之和,这里有一个迹的概念可以直接表示对角线元素之和: t r ( A ) = ∑ i = 0 n a i i tr(A) = \sum\limits_{i=0}^{n} a_{ii} tr(A)=i=0∑naii,表示矩阵 A A A对角线元素之和。
定义 k k k时刻的误差协方差阵为 P k P_k Pk, t r ( P k ) tr(P_k) tr(Pk)表示方差之和,期望取到最优的分配权重 K k K_k Kk使方差之和最小,也就是迹最小,使误差状态 e k e_k ek方差趋于0,让估计值尽量平滑。
用数学语言表示上述思想
系统定义
x
k
=
A
x
k
−
1
+
B
u
k
−
1
+
w
k
−
1
z
k
=
H
x
k
+
v
k
\begin{aligned} &x_k = Ax_{k-1} + Bu_{k-1} + w_{k-1}\\ &z_k = Hx_k + v_{k} \end{aligned}
xk=Axk−1+Buk−1+wk−1zk=Hxk+vk
式中,
x
k
x_k
xk表示状态真值,是无法得到的,只能通过量测或者估算的手段得到估计值;
A
,
B
A, B
A,B表示系统矩阵,可以看现代控制理论;
w
k
−
1
∼
N
(
0
,
Q
)
w_{k-1}\sim N(0, Q)
wk−1∼N(0,Q)表示服从高斯分布,均值为0协方差为
Q
Q
Q的系统噪声,因为噪声是多维的所以用协方差阵而不是方差;
z
k
z_k
zk表示系统状态的量测输出,即通过传感器什么的测量到的值;
H
H
H表示量测矩阵,表示系统状态
x
k
x_k
xk和量测值之间的变换关系;
v
k
∼
N
(
0
,
R
)
v_{k} \sim N(0, R)
vk∼N(0,R)表示服从高速分布,均值为0协方差为
R
R
R量测噪声,表示传感器的特性。
推导误差协方差阵
状态的估计误差
e
k
e_k
ek为:
e
k
=
x
k
−
x
^
k
=
x
k
−
(
x
^
k
−
+
K
k
(
z
k
−
H
x
^
k
−
)
)
=
x
k
−
x
^
k
−
−
K
k
H
(
x
k
−
x
^
k
−
)
+
K
k
v
k
=
(
I
−
K
k
H
)
(
x
k
−
x
^
k
−
)
+
K
k
v
k
=
(
I
−
K
k
H
)
e
k
−
+
K
k
v
k
\begin{aligned} e_k &= x_k - \hat{x}_k\\ &= x_k - (\hat{x}_k^- + K_k(z_k - H\hat{x}_k^-))\\ &= x_k - \hat{x}_k^- - K_kH(x_k - \hat{x}_k^-) + K_kv_k\\ &= (I - K_kH)(x_k - \hat{x}_k^-) + K_kv_k\\ &= (I - K_kH)e_k^- + K_kv_k \end{aligned}
ek=xk−x^k=xk−(x^k−+Kk(zk−Hx^k−))=xk−x^k−−KkH(xk−x^k−)+Kkvk=(I−KkH)(xk−x^k−)+Kkvk=(I−KkH)ek−+Kkvk
式中,
I
I
I表示单位阵;
x
^
k
\hat{x}_k
x^k表示状态的估计值,就是我们最后要求的值;
e
k
−
=
x
k
−
x
k
−
e_k^- = x_k - x_k^-
ek−=xk−xk−表示先验状态的估计误差,
x
k
−
x_k^-
xk−表示先验的预测状态。
误差的协方差阵为:
P
k
=
E
(
e
k
e
k
T
)
=
E
[
(
(
I
−
K
k
H
)
e
k
−
+
K
k
v
k
)
(
(
I
−
K
k
H
)
e
k
−
+
K
k
v
k
)
T
]
=
E
[
(
I
−
K
k
H
)
e
k
−
e
k
−
T
(
I
−
K
k
H
)
T
]
+
E
[
(
I
−
K
k
H
)
e
k
−
v
k
T
K
k
T
]
+
E
[
K
k
v
k
e
k
−
T
(
I
−
K
k
H
)
T
]
+
E
[
K
k
v
k
v
k
T
K
k
T
]
=
(
I
−
K
k
H
)
E
[
e
k
−
e
k
−
T
]
(
I
−
K
k
H
)
T
+
(
I
−
K
k
H
)
E
[
e
k
−
v
k
T
]
K
k
T
+
K
k
E
[
v
k
e
k
−
T
]
(
I
−
K
k
H
)
T
+
K
k
E
[
v
k
v
k
T
]
K
k
T
=
(
I
−
K
k
H
)
P
k
−
(
I
−
K
k
H
)
T
+
K
k
R
K
k
\begin{aligned} P_k = E(e_ke_k^T) &= E[((I - K_kH)e_k^- + K_kv_k)((I - K_kH)e_k^- + K_kv_k)^T]\\ &= E[(I - K_kH)e_k^- e_k^{-T}(I - K_kH)^T] + E[(I - K_kH)e_k^-v_k^TK_k^T] + E[K_kv_ke_k^{-T}(I-K_kH)^T] + E[K_kv_kv_k^TK_k^T]\\ &= (I - K_kH)E[e_k^- e_k^{-T}](I - K_kH)^T + (I - K_kH)E[e_k^-v_k^T]K_k^T + K_kE[v_ke_k^{-T}](I - K_kH)^T + K_kE[v_kv_k^T]K_k^T\\ &= (I - K_kH)P_k^-(I - K_kH)^T + K_kRK_k \end{aligned}
Pk=E(ekekT)=E[((I−KkH)ek−+Kkvk)((I−KkH)ek−+Kkvk)T]=E[(I−KkH)ek−ek−T(I−KkH)T]+E[(I−KkH)ek−vkTKkT]+E[Kkvkek−T(I−KkH)T]+E[KkvkvkTKkT]=(I−KkH)E[ek−ek−T](I−KkH)T+(I−KkH)E[ek−vkT]KkT+KkE[vkek−T](I−KkH)T+KkE[vkvkT]KkT=(I−KkH)Pk−(I−KkH)T+KkRKk
式中,
E
(
⋅
)
E(\cdot)
E(⋅)表示对括号内的变量求期望。这里
P
k
−
=
E
[
e
k
−
e
k
−
T
]
P_k^- = E[e_k^-e_k^{-T}]
Pk−=E[ek−ek−T],表示先验状态误差协方差;因为
e
k
−
e_k^-
ek−和
v
k
v_k
vk不相关,所以其协方差为
E
[
e
k
−
v
k
T
]
=
E
[
v
k
e
k
−
T
]
=
0
E[e_k^-v_k^T] = E[v_ke_k^{-T}] = 0
E[ek−vkT]=E[vkek−T]=0;
R
=
E
[
v
k
v
k
T
]
R = E[v_kv_k^T]
R=E[vkvkT]为量测噪声的协方差阵。那么上面的误差协方差阵
P
k
P_k
Pk为:
P
k
=
E
(
e
k
e
k
T
)
=
(
I
−
K
k
H
)
P
k
−
(
I
−
K
k
H
)
T
+
K
k
R
K
k
T
=
P
k
−
−
K
k
H
P
k
−
−
P
k
−
H
T
K
k
T
+
K
k
H
P
k
−
H
T
K
k
T
+
K
k
R
K
k
T
(2)
\begin{aligned} P_k = E(e_ke_k^T) &= (I - K_kH)P_k^-(I - K_kH)^T + K_k R K_k^T\\ &= P_k^- - K_kHP_k^- - P_k^-H^TK_k^T + K_kHP_k^-H^TK_k^T + K_kRK_k^T \tag{2} \end{aligned}
Pk=E(ekekT)=(I−KkH)Pk−(I−KkH)T+KkRKkT=Pk−−KkHPk−−Pk−HTKkT+KkHPk−HTKkT+KkRKkT(2)
至此,定义了目标,让协方差阵
P
k
P_k
Pk的迹最小,同时也给出了协方差阵
P
k
P_k
Pk的计算方式。
求解最优 K k K_k Kk使 t r ( P k ) tr(P_k) tr(Pk)最小
卡尔曼滤波也是一个优化的过程,是将误差协方差矩阵
P
k
P_k
Pk的迹(各状态量误差的方差之和)作为优化目标函数,卡尔曼增益
K
k
K_k
Kk作为决策变量,找到最优的
K
k
K_k
Kk使误差方差之和最小。根据式(2),
P
k
P_k
Pk的迹为:
t
r
(
P
k
)
=
t
r
(
P
k
−
)
−
2
t
r
(
K
k
H
P
k
−
)
+
t
r
(
K
k
H
P
k
−
H
T
K
k
T
)
+
t
r
(
K
k
R
K
k
T
)
tr(P_k) = tr(P_k^-) - 2tr(K_kHP_k^-) + tr(K_kHP_k^-H^TK_k^T) + tr(K_kRK_k^T)
tr(Pk)=tr(Pk−)−2tr(KkHPk−)+tr(KkHPk−HTKkT)+tr(KkRKkT)
令 t r ( P k ) tr(P_k) tr(Pk)关于 K k K_k Kk的偏导为0,可以求得 t r ( P k ) tr(P_k) tr(Pk)关于 K k K_k Kk的极值点,一般我们期望这是一个极小值点,可以求二阶偏导来看具体情况,如果二阶偏导大于0,那么就是极小值。网上很多资料都是直接给一阶偏导为0的点,没说明二阶偏导的正负情况,即并未证明是极小值。从结论来说这边一阶偏导为0肯定是极小值,如何证明好像没找到严格的推导qAq。(文章最后我放了简单的一些讨论,但不知道咋证明,有大佬说下嘛。)
注:对迹求导的公式
∂
t
r
(
A
B
)
∂
A
=
B
T
,
∂
t
r
(
A
B
A
T
)
∂
A
=
2
A
B
\frac{\partial tr(AB)}{\partial A} = B^T, \frac{\partial tr(ABA^T)}{\partial A} = 2AB
∂A∂tr(AB)=BT,∂A∂tr(ABAT)=2AB
令
t
r
(
P
k
)
tr(P_k)
tr(Pk)关于
K
k
K_k
Kk的偏导为0,即可求得
K
k
K_k
Kk的最优值:
∂
t
r
(
P
k
)
∂
K
k
=
−
2
(
H
P
k
−
)
T
+
2
K
k
H
P
k
−
H
T
+
2
K
k
R
=
0
\frac{\partial tr(P_k)}{\partial K_k} = -2(HP_k^-)^T + 2K_kHP_k^-H^T + 2K_kR = 0
∂Kk∂tr(Pk)=−2(HPk−)T+2KkHPk−HT+2KkR=0
K k = P k − H T H P k − H T + R = P k − H T ( H P k − H T + R ) − 1 (3) \begin{aligned} K_k &= \frac{P_k^- H^T}{HP_k^- H^T + R}\\ &= P_k^-H^T(HP_k^- H^T + R)^{-1} \tag{3} \end{aligned} Kk=HPk−HT+RPk−HT=Pk−HT(HPk−HT+R)−1(3)
把式(3)代入式(2)中,可以得到误差协方差阵
P
k
P_k
Pk的更新公式:
P
k
=
P
k
−
−
K
k
H
P
k
−
−
P
k
−
H
T
K
k
T
+
K
k
H
P
k
−
H
T
K
k
T
+
K
k
R
K
k
T
=
P
k
−
−
K
k
H
P
k
−
−
P
k
−
H
T
K
k
T
+
K
k
(
H
P
k
−
H
T
+
R
)
K
k
T
=
P
k
−
−
K
k
H
P
k
−
−
P
k
−
H
T
K
k
T
+
P
k
−
H
T
K
k
T
=
(
I
−
K
k
H
)
P
k
−
\begin{aligned} P_k &= P_k^- - K_kHP_k^- - P_k^-H^TK_k^T + K_kHP_k^-H^TK_k^T + K_kRK_k^T\\ &= P_k^- - K_kHP_k^- - P_k^-H^TK_k^T + K_k(HP_k^-H^T + R)K_k^T\\ &= P_k^- - K_kHP_k^- - P_k^-H^TK_k^T + P_k^- H^TK_k^T\\ &= (I - K_kH)P_k^- \end{aligned}
Pk=Pk−−KkHPk−−Pk−HTKkT+KkHPk−HTKkT+KkRKkT=Pk−−KkHPk−−Pk−HTKkT+Kk(HPk−HT+R)KkT=Pk−−KkHPk−−Pk−HTKkT+Pk−HTKkT=(I−KkH)Pk−
至此,找到了最优的分配权重
K
k
K_k
Kk,即卡尔曼增益。
计算先验协方差阵 P k − P_k^- Pk−
在上面卡尔曼增益
K
k
K_k
Kk和误差协方差阵
P
k
P_k
Pk的计算中,还有先验协方差阵
P
k
−
P_k^-
Pk−未知。先验协方差阵就是真值
x
k
x_k
xk与先验状态
x
^
k
−
\hat{x}_k^-
x^k−之间的误差协方差阵。前面已经定义估计误差
e
k
=
x
k
−
x
^
k
−
1
e_k = x_k - \hat{x}_{k-1}
ek=xk−x^k−1,那么先验状态误差
e
k
−
e_k^-
ek−为:
x
k
=
A
x
k
−
1
+
B
u
k
−
1
+
w
k
−
1
x_k = Ax_{k-1} + Bu_{k-1} + w_{k-1}\\
xk=Axk−1+Buk−1+wk−1
x ^ k − = A x ^ k − 1 + B u k − 1 (4) \hat{x}_k^- = A\hat{x}_{k-1} + Bu_{k-1} \tag{4} x^k−=Ax^k−1+Buk−1(4)
e
k
−
=
x
k
−
x
^
k
−
=
A
(
x
k
−
1
−
x
^
k
−
1
)
+
w
k
−
1
=
A
e
k
−
1
+
w
k
−
1
\begin{aligned} e_k^- = x_k - \hat{x}_k^- &= A(x_{k-1} - \hat{x}_{k-1}) + w_{k-1}\\ &= Ae_{k-1}+w_{k-1} \end{aligned}
ek−=xk−x^k−=A(xk−1−x^k−1)+wk−1=Aek−1+wk−1
其中
x
^
k
−
\hat{x}_k^-
x^k−为状态的预测值,即通过系统模型
A
,
B
A,B
A,B矩阵以及上一时刻的估计状态
x
^
k
−
1
\hat{x}_{k-1}
x^k−1预测出来这一时刻的值。我们最终要赋予这个值和量测值
z
k
z_k
zk不同的权重计算这一时刻的估计状态
x
^
k
\hat{x}_k
x^k。
那么先验协方差阵为:
P
k
−
=
E
(
e
k
−
e
k
−
T
)
=
E
[
(
A
e
k
−
1
+
w
k
−
1
)
(
A
e
k
−
1
+
w
k
−
1
)
T
]
=
E
[
A
e
k
−
1
e
k
−
1
T
A
T
+
A
e
k
−
1
w
k
−
1
+
w
k
−
1
T
e
k
−
1
T
A
T
+
w
k
−
1
w
k
−
1
T
]
=
E
[
A
e
k
−
1
e
k
−
1
T
A
T
]
+
E
[
A
e
k
−
1
w
k
−
1
]
+
E
[
w
k
−
1
T
e
k
−
1
T
A
T
]
+
E
[
w
k
−
1
w
k
−
1
T
]
=
A
E
[
e
k
−
1
e
k
−
1
T
]
A
T
+
E
[
w
k
−
1
w
k
−
1
T
]
=
A
P
k
−
1
A
T
+
Q
(5)
\begin{aligned} P_k^- &= E(e_k^-e_k^{-T})\\ &= E[(Ae_{k-1} + w_{k-1})(Ae_{k-1} + w_{k-1})^T]\\ &= E[Ae_{k-1}e_{k-1}^TA^T + Ae_{k-1}w_{k-1} + w_{k-1}^Te_{k-1}^TA^T + w_{k-1}w_{k-1}^T]\\ &= E[Ae_{k-1}e_{k-1}^TA^T] + E[Ae_{k-1}w_{k-1}] + E[w_{k-1}^Te_{k-1}^TA^T] + E[w_{k-1}w_{k-1}^T]\\ &= AE[e_{k-1}e_{k-1}^T]A^T + E[w_{k-1}w_{k-1}^T]\\ &= AP_{k-1}A^T + Q \end{aligned} \tag{5}
Pk−=E(ek−ek−T)=E[(Aek−1+wk−1)(Aek−1+wk−1)T]=E[Aek−1ek−1TAT+Aek−1wk−1+wk−1Tek−1TAT+wk−1wk−1T]=E[Aek−1ek−1TAT]+E[Aek−1wk−1]+E[wk−1Tek−1TAT]+E[wk−1wk−1T]=AE[ek−1ek−1T]AT+E[wk−1wk−1T]=APk−1AT+Q(5)
到这里为止,把式(2)~(5)代入到式(1)中就能完成对当前状态真值
x
k
x_k
xk的估计,实现卡尔曼滤波,得到估计值
x
^
k
\hat{x}_{k}
x^k
写在最后
列一下网上能查到的卡尔曼滤波5条公式,结论:
x
^
k
−
=
A
x
^
k
−
1
+
B
u
k
−
1
P
k
−
=
A
P
k
−
1
A
T
+
Q
K
k
=
P
k
−
H
T
H
P
k
−
H
T
+
R
x
^
k
=
x
^
k
−
+
K
k
(
z
k
−
H
k
x
^
k
−
)
P
k
=
(
I
−
K
k
H
k
)
P
k
−
\begin{aligned} &\hat{x}_k^- = A\hat{x}_{k-1} + Bu_{k-1}\\ &P_k^- = AP_{k-1}A^T + Q\\ &K_k = \frac{P_k^- H^T}{HP_k^- H^T + R}\\ &\hat{x}_k = \hat{x}_k^- + K_k(z_k - H_k\hat{x}_k^-)\\ &P_k = (I - K_kH_k)P_k^- \end{aligned}
x^k−=Ax^k−1+Buk−1Pk−=APk−1AT+QKk=HPk−HT+RPk−HTx^k=x^k−+Kk(zk−Hkx^k−)Pk=(I−KkHk)Pk−
上面的推导过程没有按照这5条公式的顺序来,而是从最终目的出发,以得到状态的估计值
x
^
k
\hat{x}_k
x^k为目标,先推导与计算
X
^
k
\hat{X}_k
X^k最相关的卡尔曼增益
K
k
K_k
Kk,推导过程中引出了误差协方差阵
P
k
P_k
Pk的计算,在计算
P
k
P_k
Pk过程中又引出了先验状态
x
^
k
−
\hat{x}_k^-
x^k−和先验误差协方差阵
P
k
−
P_k^-
Pk−的计算方式,最终完成卡尔曼滤波的推导。
接下来讨论一下卡尔曼增益计算时候的二阶偏导的性质,我们期望其二阶偏导为正,那么一阶偏导为0算出来的
K
k
K_k
Kk能让误差方差之和最小,即达到最优。二阶偏导为:
∂
2
t
r
(
P
k
)
∂
K
k
2
=
2
H
P
k
−
H
T
+
2
R
\frac{\partial^2 tr(P_k)}{\partial K_k^2} = 2HP_k^-H^T + 2R
∂Kk2∂2tr(Pk)=2HPk−HT+2R
上面这个二阶偏导没法直接考察正定还是负定,那么从定义来看
P
k
−
=
E
[
x
k
−
x
k
−
T
]
P_k^-=E[x_k^- x_k^{-T}]
Pk−=E[xk−xk−T]为先验状态协方差阵,
R
R
R为量测噪声协方差阵,在网上查了一下协方差阵的正定性,说协方差阵一定半正定,即从定义来说
P
k
−
≥
0
P_k^- \geq 0
Pk−≥0,
P
k
≥
0
P_k \geq 0
Pk≥0,
Q
≥
0
Q \geq 0
Q≥0,
R
≥
0
R \geq 0
R≥0。那么这里的二阶偏导至少就是半正定的,一般来说也不会取到半正定的那个等于0的值,因此取一阶偏导为0时的
K
k
K_k
Kk能让
P
k
P_k
Pk取到极小值。这个说明过程非常不严谨,但至少对取一阶偏导为0时取到极小值进行了补充说明,不知道有没有更严格一点的证明。
我觉得如何说明 P k P_k Pk和 P k − P_k^- Pk−是正定的才是卡尔曼滤波的本质,因为这里决定了卡尔曼滤波状态的最优性和收敛性。
但是对于把卡尔曼滤波作为工具使用来说,掌握5条公式和个变量的含义就够了,再进一步也就是把上面的推导过程消化了,对于工程使用来说足够了。





















 40万+
40万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








