10-2- Logistic Regression Error
我们现在开始讲 Logistic Regression ,跟我们之前学过的 Linear Regression 和 Linear Classification 稍微做个对照。
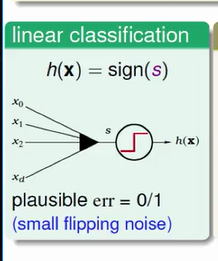
共同的事情是什么?大家都要用 wTX 计算一个分数,算了分数以后做什么?Linear Classification 取这个分数是大于 0 ,还是小于 0 的,来做 Linear Classification 的动作,我们说,在那个时候呢,我们做资料分类的动作,最简单,最能说说服我们的 err 是 err0/1 , 意思是说我今天到底是分对了,还是分错了,是 err0/1 这样的错误。

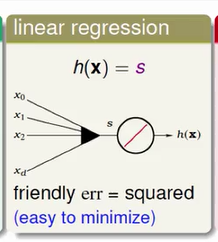
今天如果是 Linear Regression 会怎么样?Linear Regression 就不会像 Linear Classification 那样左边取一个 sign , 我用一个阶梯状的函数来代表 sign 函数,那 Linear Regression 加完之后,我左边那些箭头代表加完之后,s 它就直接输出了, 我这边画一个斜线,斜线的意思是我这边加完之后,就直接输出 s 了,这是一个 identity 的 function ,那我们那时候说,我们用的 error 是什么呢?我们用的 error 是squared error ,最后导出这个简洁的 Linear Regression 演算法 , 这是用 squared error 重要的理由,它很容易 minimize 。
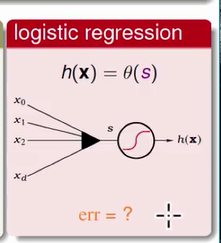
好,那 Logistical Regression 呢?我们现在知道的事情是它算完分数之后,它要透过一个 sigmod ,一个 s 型的 Logistical 函数来做出所有动作。我们要问的问题是这样,那它的 error funcation 应该长什么样子?或者说我们要怎样去define 我们要 minimize 的那个 E(in) 到底是个什么东西?
要回答这样的问题,对于 Logistic 这样的问题,我们的目标是 P 的时候,对于 P 来说,有一种特殊的方法来定义我们的 error function 长什么样子?我们有兴趣的 target function 是长这个样子: f(x)=P(+1|x) ,我们的 target function 是 P of +1 ,given x ,我如果把它反着写过来,就是 y 有两种:一种是 +1,一种的 -1,P of +1 ,given x 是什么?你会说,这太简单了,等号反过来,+1 given x ,f(x); 相反的是 P of -1 ,given x 是什么?是 1-f(x) 。因为几率加起来要是 1 ,所以 + 1 ,given x 是什么,-1 ,given x 就是它反过来 的部分。
那我们来看看,有了这样的概念之后,我就问你了,如果有一个资料,长得是这个样子, x1 是圈圈, x2 是叉叉,一直到 xN 是叉叉。那这个资料产生的几率是多少?你有那个 f(x) , 你可以算 f(x) 到底是怎么产生这个资料?这个资料产生的几率是多少?根据我们的设定的话,因为 id 等等这些,所以你知道资料产生的几率是什么?你要先有 x1 啊,所以从 x1 产生了 x1 ,然后呢,有了 x1 之后,产生 y1 , 有圈圈 given x1 , y1 是圈圈啊,然后呢,再来,你有 x2 ,产生 x2 ,然后 y2 ,given x2 , …… 一路下来,那根据上面的式子的话,你就可以把圈圈 given x1 换成 f(x), 把叉叉 given x1 换成 1- f(x) ,所以呢,大家再仔细的看一次,我原来说我产生我资料的几率是这样,现在根据我刚才讲的,我的 f(x) 和我的 P 是密不可分的,密不可分的话,我们就可以把 P 换成 f(x) 。
P 换成 f(x) 是什么意思?那我们现在来想啦,我今天有的不是 f(x) , 也就是说 f(x) 是我们不知道的,我们想要的东西是 h, 不然这样好啦,我们让 h 假扮一下 f(x) , 会发生什么事?假扮一下 f(x),如果我们假装 h 就是 f(x) 的话,我们就可以看看说 h 产生一模一样的资料的可能性是多少,我们一般把可能性叫做 likelihood ,到底有多可能 h 也会产生一模一样的 f(x) 的资料
好,所以这是一个假装的动作,假装 h 就是我们的 f(x) ,我们来看看到底发生了什么事情。事情很简单,我们假装 h 就是 f(x) 的话,那左边的那个式子里是 f(x) , 我只要做取代的动作就好了,我就把所有看到 f(x) 的地方通通取代成 h ,列出这一串下来,就是 h 也产生了这一连串资料的可能性。
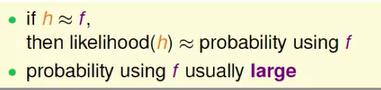
我们来想想看,如果今天我们的 h 和 f(x) 很接近的话,注意到 error function 衡量的是什么,error function 衡量的是 H 和 f(x) 是不是很接近,如果今天 h 和 f(x) 很接近的话,那么 f(x) 产生这些资料的可能性应该就和真正的 h 产生这些资料的可能性很接近。
如果 h 和 f(x) 很接近的话,那么 f(x) 的几率是多少,h 的几率就是多少,因为 f(x) 已经真正被我们假设是产生这些资料的,通常 f(x) 真正产生这些资料的几率是很大的,也就是说你真正拿了 f(x) 来产生这些资料,回头来看,f(x) 真正产生这些资料的几率是很大的。
从这样的观念,我们就可以推演出一个适当的 error function 有着如下形式,我们说 f(x) 的可能性和 h 是类似的,如果今天是一个好的 h 的话,f(x) 的几率应该是很大的,所以我们怎么样找一个好的 h 当作我们的 g 呢?我们要的 g 就是可能性最高的那个,所以我们在 h 里卖弄找一个可能性最高的,那个当成我们的 g 就好了。
也就是什么意思呢,如果我们今天看到的 h ,我们今天看一个特别的 h ,我们的 h 是 Logistic Function ,我们的 Logistic Regression 里面有 h 的话,它的特色性质是它有一个对称性,即 1−h(x)=h(−x) 。
那我们就可以把原来的 h 的可能性应用 Logistic Function 的对成性写成另外一种形式。我这边有 N 笔资料的话,我有 N 项在里面,第一项跟 x1 有关,第二项跟 x2 有关, 一直到第 N 项跟 xN 有关,大家看到这里我把 P(x1) , P(x2) , P(x3) 画成了灰色的, 因为对所有的 H 来说,他们都是一样的。
因为我今天是衡量可能性,用的都是同样的 x1) 一直到 xn ,既然是一样的话,我就不用在意它了,我们要在意的是每个 h 不一样的地方在哪里,不一样的地方只有后面乘上额这些项,应用对称性,我们可以把 h(1- x) 用 h(-x) 替换,最后得到的式子如下所示:
除了灰色我们不在意的部分外,这边有一个 h(+ x1) ) ,表示它是圈圈,然后我们计算它的 h 值是多少,第二项呢,它是叉叉,我们计算它的 h 值是多少 ……
整理下来我们就知道,如果今天是一个 Logistic function 的话,想知道可能性,可能性正比于我把所有的 h 乘起来,我在每一笔资料上衡量 h 的值是多少,然后把它乘起来,这个就会正比于我们想要求的可能性,括号里面的式子,如果是个圈圈,就直接是 xn) ,如果是叉叉,我们就用 −xn) , 实际上是代表 1−h(xn) 的意思,这样乘起来,会是我们的可能性。
所以我们有兴趣的事情就是找一个 h ,让这个可能性是最大的,我们把 跟 h 有关的 w 的式子代替 h 。
我做的事情实际上是这样
上面的式子里面有连乘,我们想把连乘换成连加,最简单的方法是取 log ,取了 log 后,我们进一步简化式子,在 Linear Regression 和 Linear Classification 中,我们做的都是最小化动作,我们看的是 E(in) , 我们要做最小化的动作,而不是最大化的动作,我们乘上一个符号后,从求最大化转换成求最小化。
最终得到的式子是
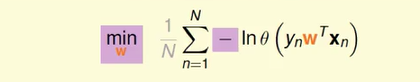
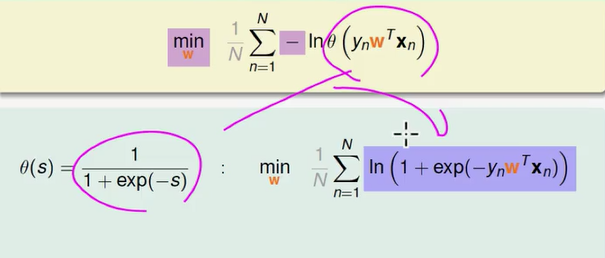
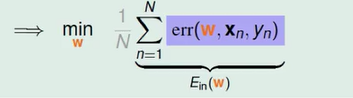
为了把式子变成我们熟悉的 Linear Regression 的长相,我这边偷偷的 偷偷的加了一个灰色的 1/N,这个常数 1/N 并不是很重要,因为它对所有的 w 都做一样的操作,放在这边,等一下我们的式子会比较清楚,所以这个是我们在 Logistic Regression 中想要解决的问题,找一个 w 来让右边的式子取最小值。把 θ 的 定义加进来带入,我们的式子又变了样子。
进一步整理得到
把这些 error 加起来,取平均就是我们 E(in) 的部分 , E(in) 应该要包含 1/N 的部分。
所以这个 pointwise err function 在传统上叫做 cross-entropy error。













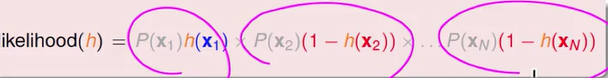
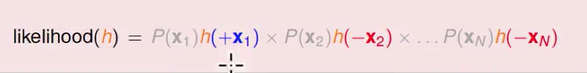
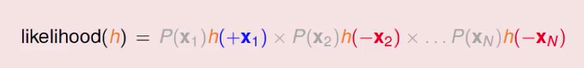
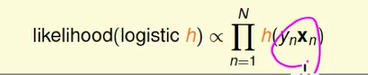

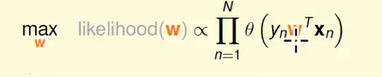
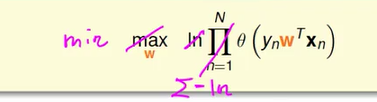















 1653
1653

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








