机器学习算法入门之(二) 决策树算法

机器学习算法入门之(二) 决策树算法

本文简单描述了经典的分类算法：决策树算法。

机器学习基本概念

定义学习：针对经验E (experience) 和一系列的任务 T (tasks) 和一定表现的衡量 P，如果随之经验E的积累，针对定义好的任务T可以提高表现P，就说计算机具有学习能力

例子： 下棋，语音识别，自动驾驶汽车等

机器学习算法评估标准：
- 准确性
- 速度
- 鲁棒性
- 可规模性
- 可解释性

python机器学习包：scikit-learn: Machine Learning in Python。或者可以使用Anaconda，这个包集成了机器学习的所有环境，甚至包括python的解释器。但是我并没有用过，只是用pip安装了scikit-learn。

同时还使用了Graphviz来进行可视化。安装完成之后，将安装的路径’C:\Program Files (x86)\Graphviz2.38\bin;’加到windows的环境变量path中即可通过命令行对数据进行可视化。

dot -Tpdf iris.dot -o outpu.pdf

熵（entropy）

信息熵：一个随机变量的熵越大，它的不确定性就越大，正确估计其值的可能性就越小，需要越大的信息量用以确实其值。一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情（比如我们一无所知的事情）需要了解大量信息。信息熵描述了不确定性的多少。越不确定，熵越大。

若$X$是一个离散型随机变量，其概率分布为：

$$p(x)=P(X=x), x\in X$$ 则X的熵

$$H(x)=-\sum_{x\in X}^{ }p(x)\log_{2}p(x)$$

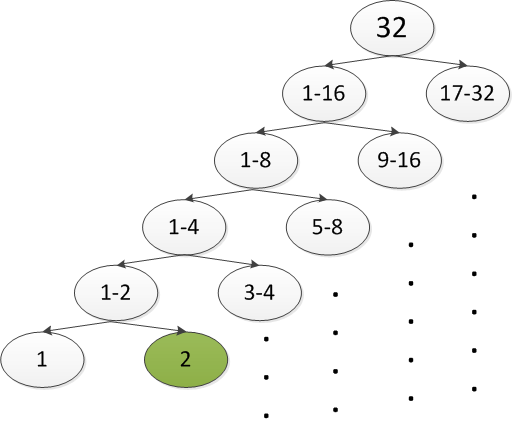
比如，猜世界杯冠军。假设我们对所有球队都一无所知（即每支球队夺冠的可能性相同），需要猜多少次？

从上图可以看出，通过$\log_{2}32=5$次猜测（二分），即可猜出结果。
这个例子中，熵$H(x)=-(P_1*\log_{2}P_1+P_2*\log_{2}P_2+...+P_{32}*\log_{2}P_{32})=5$（不知道这里的5和之前的5有没有什么关联，望指教）

互信息（信息增益）：衡量通过信道传输进行通信后所消除的不确定性的大小，定义为

$$I(U, V)=H(U)-H(U|V)$$
表示接收到 $V$后获得的关于$U$的信息量，是不确定性的消除，是信宿端（接收端）所获得的信息量，其中 $$H(U|V)=-\sum_{v_i\in V}^{ }\left [\ p(v_i)\sum_{u_j\in U}^{ }p(u_j|v_i)\log_{2}p(u_j|v_i) \right]$$

ID3决策树算法

ID3算法使用信息增益（Information Gain）作为属性选择的度量。算法的思想是，找出最有判别力的因素将数据分成多个子集，对每个子集重复上述步骤，直到所有子集仅含同类型数据。然后用得到的决策树对新样本进行分类。

为了描述方便，我们首先引入我们的例子。

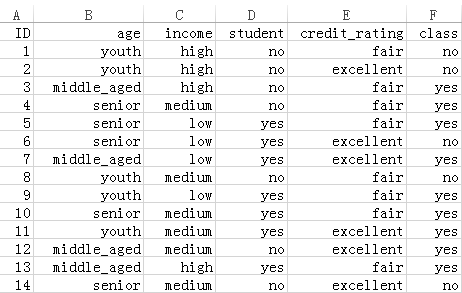
如图所示，这组数据有14个样本，4个特征。最后的class标记了是否去运动。数据集提供如下：

ID,age,income,student,credit_rating,class
1,youth,high,no,fair,no
2,youth,high,no,excellent,no
3,middle_aged,high,no,fair,yes
4,senior,medium,no,fair,yes
5,senior,low,yes,fair,yes
6,senior,low,yes,excellent,no
7,middle_aged,low,yes,excellent,yes
8,youth,medium,no,fair,no
9,youth,low,yes,fair,yes
10,senior,medium,yes,fair,yes
11,youth,medium,yes,excellent,yes
12,middle_aged,medium,no,excellent,yes
13,middle_aged,high,yes,fair,yes
14,senior,medium,no,excellent,no

各数据的属性及其取值分别为：
outlook = { sunny, overcast, rain }
temperature = { hot, mild, cool }
humidity = { high, normal }
wind = { yes, no }
最终的分类$U$有两类：{ yes, no }

$$H(U)=-\frac{9}{14}\log_{2}(\frac{9}{14})-\frac{5}{14}\log_{2}(\frac{5}{14})=0.9403$$

$$H(U|outlook)=\begin{matrix} \frac{5}{14}\times (-\frac{2}{5}\log_{2}\frac{2}{5}-\frac{3}{5}\log_{2}\frac{3}{5})\\ +\frac{4}{14}\times (-\frac{4}{4}\log_{2}\frac{4}{4}-\frac{0}{4}\log_{2}\frac{0}{4})\\ +\frac{5}{14}\times (-\frac{3}{5}\log_{2}\frac{3}{5}-\frac{2}{5}\log_{2}\frac{2}{5})\\ \end{matrix}=0.694 bits$$
$I(U，outlook)=H(U)-H(U|outlook)=0.9403-0.694=0.2463$
同理可得：
$I(U，temperature)=0.029$
$I(U，humidity)=0.151$
$I(U，windy)=0.048$
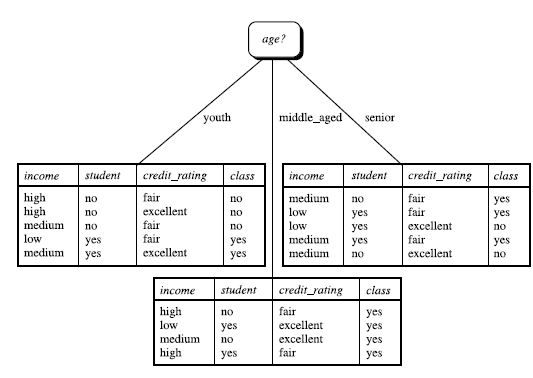
所以选择outlook作为决策树的根结点，将其三个取值分别作为三个分支，并划分原数据集合为三个子集，如下图所示：

判断子集中各记录是否属于同一类别（如middle_aged子集中的记录），若是则在树上作标记，否则对子集重复上述步骤，直至所有叶子结点都被打上标记。

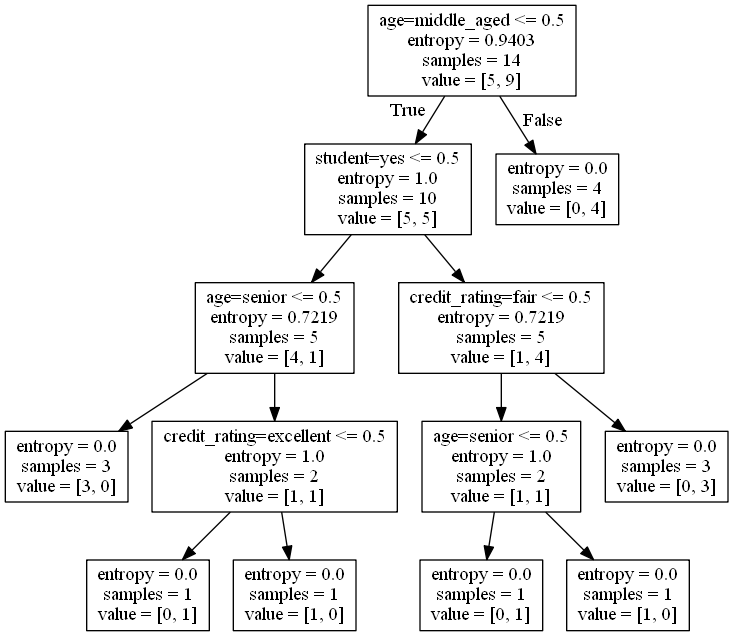
根据以上数据，我们使用ID3算法，将得到以下决策树。

常用的决策树算法有：
- ID3 (Information Gain)
- CART(gini index)
- C4.5 （gain ratio)
共同点：都是贪心算法，自上而下（Top-down approach）。
不同点：属性选择的度量方法不同。

决策树分类
优点：直观，便于理解；小规模数据集有效。
缺点：处理连续变量不好；类别较多时，错误增加的比较快；可规模性一般。

---

参考文献

1. scikit-learn: Machine Learning in Python
2. Anaconda
3. Graphviz - Graph Visualization Software
4. ID3算法图文_百度文库