图神经网络学习实践——Zachary’s karate club Problem

Together_CZ

已于 2022-05-06 13:34:50 修改

阅读量7.3k

点赞数 10

分类专栏：机器学习深度学习文章标签：神经网络学习 python

于 2020-06-02 21:22:20 首次发布

本文链接：https://blog.csdn.net/Together_CZ/article/details/106504531

版权

机器学习同时被 2 个专栏收录

284 篇文章

订阅专栏

深度学习

167 篇文章

订阅专栏

本文实践了DGL图神经网络在社交网络分类任务上的应用，通过解决扎卡里的空手道俱乐部问题，展示了如何创建图、分配节点特征、定义图卷积网络，并训练模型进行节点分类。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

图神经网络是一类比较特殊的神经网络，这里的图不同于我们卷积神经网络里面所使用到的图像，而是指的是node和edge组成的具有拓扑结构的图，这一类型的数据和应用我在平时的工作实践中接触得还是比较少的，正好就当做是学习了。

DGL是一个Python软件包，专门用于在图上进行深度学习，它构建在顶部现有的张量DL框架（例如Pytorch，MXNet）并简化了基于图的神经网络的实现。

这里DGL的安装也是很简单的，具体的安装方案可以参考这里。

windows下的安装命令如下：

pip install dgl

整体的安装是很简单的。

本文主要是实践DGL官网的教程【扎卡里的空手道俱乐部问题】。空手道俱乐部是一个社交网络，由34名成员组成，并记录俱乐部外部互动的成员之间的成对链接。俱乐部随后分为两个社区，由教员（节点0）和俱乐部主席（节点33）领导。网络的可视化如下，其颜色指示社区：

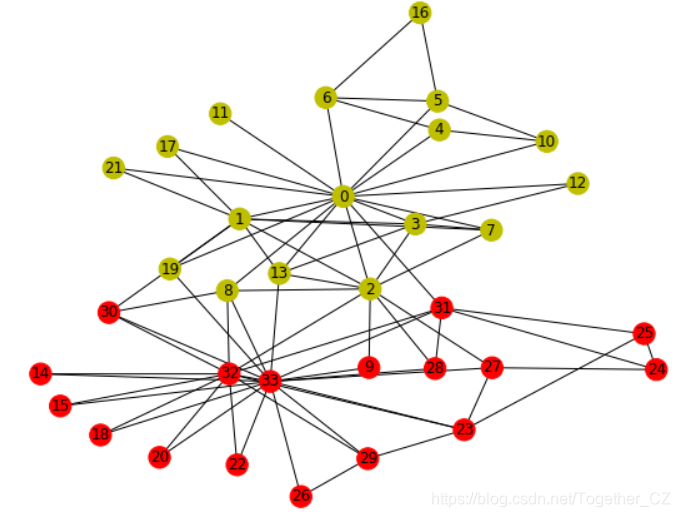
该教程的任务是预测给定社交网络本身每个成员倾向于加入哪一侧（0或33）。

Step 1: Creating a graph in DGL

首先初始化创建图，代码实现如下所示:

def build_karate_club_graph():
    '''
    所有78条边都存储在两个numpy数组中, 一个用于源端点而另一个用于目标端点
    '''
    src = np.array([1, 2, 2, 3, 3, 3, 4, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 9, 10, 10,
        10, 11, 12, 12, 13, 13, 13, 13, 16, 16, 17, 17, 19, 19, 21, 21,
        25, 25, 27, 27, 27, 28, 29, 29, 30, 30, 31, 31, 31, 31, 32, 32,
        32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33,
        33, 33, 33, 33, 33, 33, 33, 33, 33, 33])
    dst = np.array([0, 0, 1, 0, 1, 2, 0, 0, 0, 4, 5, 0, 1, 2, 3, 0, 2, 2, 0, 4,
        5, 0, 0, 3, 0, 1, 2, 3, 5, 6, 0, 1, 0, 1, 0, 1, 23, 24, 2, 23,
        24, 2, 23, 26, 1, 8, 0, 24, 25, 28, 2, 8, 14, 15, 18, 20, 22, 23,
        29, 30, 31, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30,
        31, 32])
    #边缘在DGL中是有方向的； 使它们双向
    u = np.concatenate([src, dst])
    v = np.concatenate([dst, src])
    #构建图
    return dgl.DGLGraph((u, v))

在新构建的图中打印出节点和边的数量

G = build_karate_club_graph()
print('We have %d nodes.' % G.number_of_nodes())
print('We have %d edges.' % G.number_of_edges())

结果如下所示：

接下来基于networkx来对图进行可视化，代码实现如下所示：

#通过将其转换为networkx图来可视化该图
nx_G = G.to_networkx().to_undirected()
pos = nx.kamada_kawai_layout(nx_G)
nx.draw(nx_G, pos, with_labels=True, node_color=[[.7, .7, .7]])
plt.savefig('graph.png')

结果如下所示：

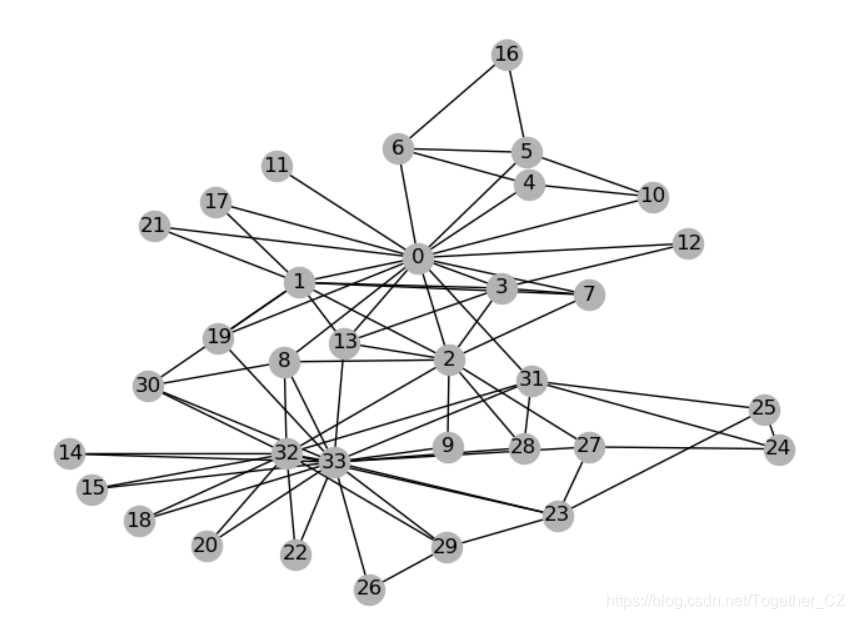
这里基于networkx绘制的是无向图。

Step 2: Assign features to nodes or edges

图神经网络将特征与节点和边关联以进行训练。对于我们的分类示例，由于没有输入功能，因此我们为每个节点分配了可学习的嵌入向量。代码实现如下所示：

embed = nn.Embedding(34, 5)  # 34 nodes with embedding dim equal to 5
G.ndata['feat'] = embed.weight
print(G.ndata['feat'][2])
print(G.ndata['feat'][[10, 11]])

结果如下所示：

Step 3: Define a Graph Convolutional Network (GCN)

要执行节点分类，请使用由Kipf和Welling开发的图卷积网络（GCN）。这是GCN框架的最简单定义。我们建议您阅读原始文章以获取更多详细信息。

如下所示：

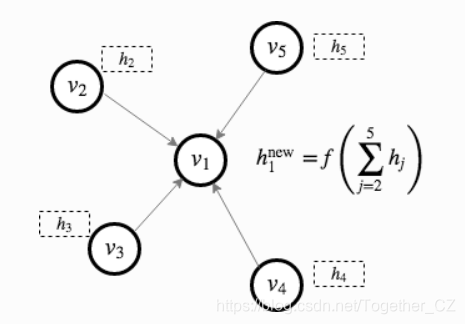
定义一个包含两个GCN层的更深入的GCN模型：

class GCN(nn.Module):
    def __init__(self, in_feats, hidden_size, num_classes):
        super(GCN, self).__init__()
        self.conv1 = GraphConv(in_feats, hidden_size)
        self.conv2 = GraphConv(hidden_size, num_classes)

    def forward(self, g, inputs):
        h = self.conv1(g, inputs)
        h = torch.relu(h)
        h = self.conv2(g, h)
        return h
#初始化网络实例
net = GCN(5, 5, 2)
print('net: ', net)

结果如下所示：

Step 4: Data preparation and initialization

我们使用可学习的嵌入来初始化节点特征。由于这是半监督设置，因此仅为教练（节点0）和俱乐部主席（节点33）分配标签。该实现如下。

inputs = embed.weight
labeled_nodes = torch.tensor([0, 33])  # only the instructor and the president nodes are labeled
labels = torch.tensor([0, 1])  # their labels are different

Step 5: Train then visualize

训练循环与其他PyTorch模型完全相同。我们（1）创建一个优化器，（2）将输入输入模型，（3）计算损失，（4）使用自动分级优化模型。

optimizer = torch.optim.Adam(itertools.chain(net.parameters(), embed.parameters()), lr=0.01)
all_logits = []
for epoch in range(50):
    logits = net(G, inputs)
    # we save the logits for visualization later
    all_logits.append(logits.detach())
    logp = F.log_softmax(logits, 1)
    # we only compute loss for labeled nodes
    loss = F.nll_loss(logp[labeled_nodes], labels)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    print('Epoch %d | Loss: %.4f' % (epoch, loss.item()))

结果如下所示：

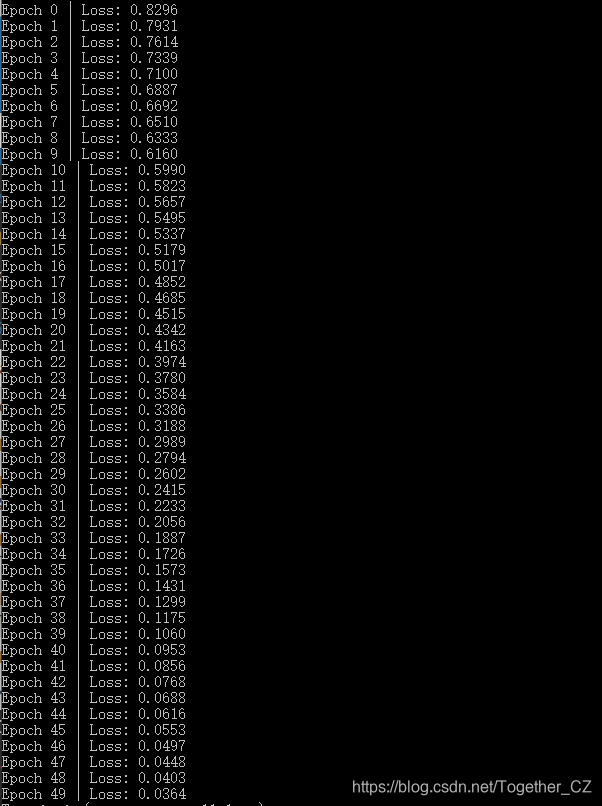
这是一个很有趣的示例，因此甚至没有验证或测试集。相反，由于模型为每个节点生成大小为2的输出特征，因此我们可以通过在2D空间中绘制输出特征来可视化。以下代码使训练过程从最初的猜测（根本没有对节点进行正确分类）到最终的结果（使节点线性可分离）动画化。

def draw(i):
    cls1color = '#00FFFF'
    cls2color = '#FF00FF'
    pos = {}
    colors = []
    for v in range(34):
        pos[v] = all_logits[i][v].numpy()
        cls = pos[v].argmax()
        colors.append(cls1color if cls else cls2color)
    ax.cla()
    ax.axis('off')
    ax.set_title('Epoch: %d' % i)
    nx.draw_networkx(nx_G.to_undirected(), pos, node_color=colors,
            with_labels=True, node_size=300, ax=ax)

fig = plt.figure(dpi=150)
fig.clf()
ax = fig.subplots()
draw(0)
plt.savefig('0.png')

结果如下所示：

以下动画显示了经过一系列训练后，模型如何正确预测社区。

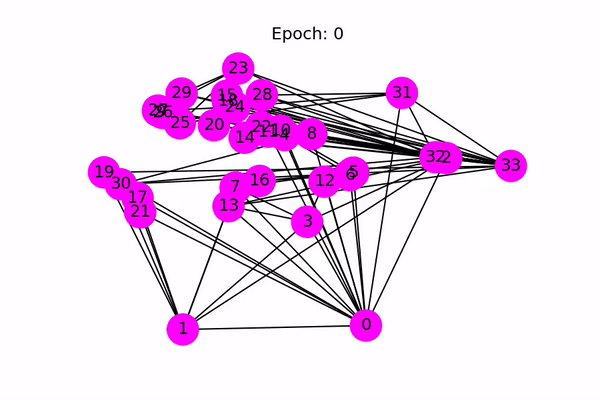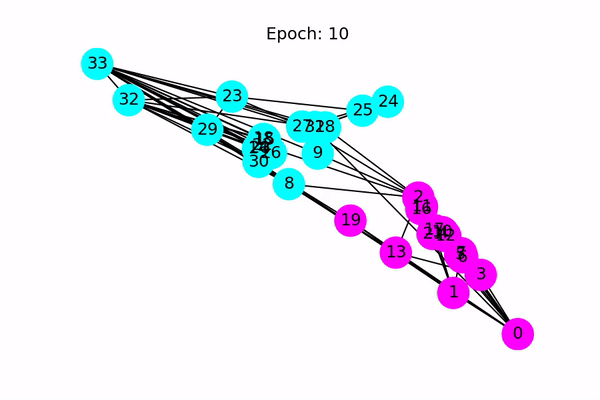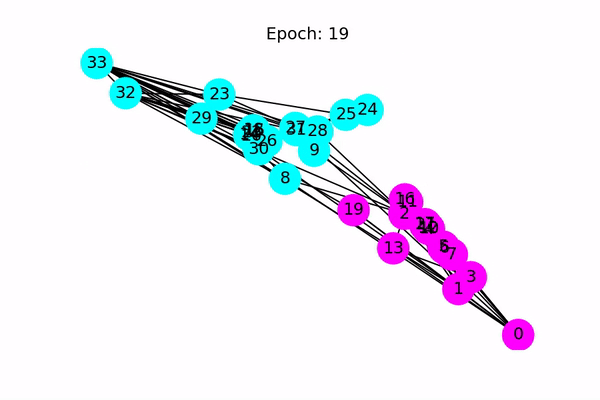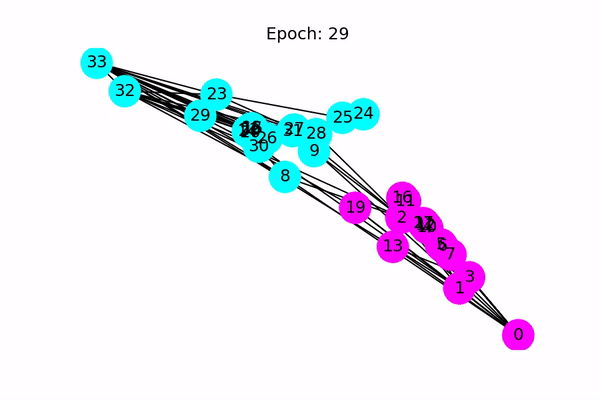
今天是图神经网络的初步实践，后面有时间会继续学习。

完整代码如下所示：

#!usr/bin/env python
#encoding:utf-8
from __future__ import division
 


"""
__Author__:沂水寒城
DGL概览:
        DGL是一个Python软件包，专门用于在图上进行深度学习，它构建在顶部现有的张量DL框架
        （例如Pytorch，MXNet）并简化了基于图的神经网络的实现。
"""


import dgl
import numpy as np
import networkx as nx
import torch
import torch.nn as nn
import torch.nn.functional as F
from dgl.nn.pytorch import GraphConv
import itertools
import matplotlib.animation as animation
import matplotlib.pyplot as plt


#Step 1: Creating a graph in DGL
def build_karate_club_graph():
    '''
    所有78条边都存储在两个numpy数组中, 一个用于源端点而另一个用于目标端点
    '''
    src = np.array([1, 2, 2, 3, 3, 3, 4, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 9, 10, 10,
        10, 11, 12, 12, 13, 13, 13, 13, 16, 16, 17, 17, 19, 19, 21, 21,
        25, 25, 27, 27, 27, 28, 29, 29, 30, 30, 31, 31, 31, 31, 32, 32,
        32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33,
        33, 33, 33, 33, 33, 33, 33, 33, 33, 33])
    dst = np.array([0, 0, 1, 0, 1, 2, 0, 0, 0, 4, 5, 0, 1, 2, 3, 0, 2, 2, 0, 4,
        5, 0, 0, 3, 0, 1, 2, 3, 5, 6, 0, 1, 0, 1, 0, 1, 23, 24, 2, 23,
        24, 2, 23, 26, 1, 8, 0, 24, 25, 28, 2, 8, 14, 15, 18, 20, 22, 23,
        29, 30, 31, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30,
        31, 32])
    #边缘在DGL中是有方向的； 使它们双向
    u = np.concatenate([src, dst])
    v = np.concatenate([dst, src])
    #构建图
    return dgl.DGLGraph((u, v))

#在新构建的图中打印出节点和边的数量
G = build_karate_club_graph()
print('We have %d nodes.' % G.number_of_nodes())
print('We have %d edges.' % G.number_of_edges())
#通过将其转换为networkx图来可视化该图
nx_G = G.to_networkx().to_undirected()
pos = nx.kamada_kawai_layout(nx_G)
nx.draw(nx_G, pos, with_labels=True, node_color=[[.7, .7, .7]])
plt.savefig('graph.png')




# Step 2: Assign features to nodes or edges
embed = nn.Embedding(34, 5)  # 34 nodes with embedding dim equal to 5
G.ndata['feat'] = embed.weight
print(G.ndata['feat'][2])
print(G.ndata['feat'][[10, 11]])





# Step 3: Define a Graph Convolutional Network (GCN)
class GCN(nn.Module):
    def __init__(self, in_feats, hidden_size, num_classes):
        super(GCN, self).__init__()
        self.conv1 = GraphConv(in_feats, hidden_size)
        self.conv2 = GraphConv(hidden_size, num_classes)

    def forward(self, g, inputs):
        h = self.conv1(g, inputs)
        h = torch.relu(h)
        h = self.conv2(g, h)
        return h
#初始化网络实例
net = GCN(5, 5, 2)
print('net: ', net)




# Step 4: Data preparation and initialization
inputs = embed.weight
labeled_nodes = torch.tensor([0, 33])  #
labels = torch.tensor([0, 1])  






# Step 5: Train then visualize
optimizer = torch.optim.Adam(itertools.chain(net.parameters(), embed.parameters()), lr=0.01)
all_logits = []
for epoch in range(50):
    logits = net(G, inputs)
    # we save the logits for visualization later
    all_logits.append(logits.detach())
    logp = F.log_softmax(logits, 1)
    # we only compute loss for labeled nodes
    loss = F.nll_loss(logp[labeled_nodes], labels)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    print('Epoch %d | Loss: %.4f' % (epoch, loss.item()))





def draw(i):
    cls1color = '#00FFFF'
    cls2color = '#FF00FF'
    pos = {}
    colors = []
    for v in range(34):
        pos[v] = all_logits[i][v].numpy()
        cls = pos[v].argmax()
        colors.append(cls1color if cls else cls2color)
    ax.cla()
    ax.axis('off')
    ax.set_title('Epoch: %d' % i)
    nx.draw_networkx(nx_G.to_undirected(), pos, node_color=colors,
            with_labels=True, node_size=300, ax=ax)

fig = plt.figure(dpi=150)
fig.clf()
ax = fig.subplots()
draw(0)
plt.savefig('0.png')




ani = animation.FuncAnimation(fig, draw, frames=len(all_logits), interval=200)
plt.savefig('1.png')