NAS：Neural Architecture Search With Reinforcement Learning——使用强化学习的神经架构搜索

最新推荐文章于 2025-02-22 13:06:42 发布

Together_CZ

最新推荐文章于 2025-02-22 13:06:42 发布

阅读量885

点赞数 26

文章标签：架构 NAS 神经架构搜索

本文链接：https://blog.csdn.net/Together_CZ/article/details/143681858

版权

神经架构搜索NAS是现代非常重要的技术手段，本文主要是对NAS论文的阅读记录，以备后续翻阅学习使用，感兴趣的话可以参考一下，如果想要进一步了解研究工作内容的话建议移步阅读原英文论文，地址在这里，如下所示：

摘要

神经网络是强大且灵活的模型，适用于图像、语音和自然语言理解中的许多困难学习任务。尽管取得了成功，神经网络的设计仍然很困难。在本文中，我们使用递归网络生成神经网络的模型描述，并通过强化学习训练这个RNN，以最大化生成的架构在验证集上的预期准确率。在CIFAR-10数据集上，我们的方法从零开始，可以设计出一种新颖的网络架构，其测试集准确率与人类发明的最佳架构相当。我们的CIFAR-10模型实现了3.65%的测试错误率，比之前使用类似架构方案的最佳模型提高了0.09%，并且速度快了1.05倍。在Penn Treebank数据集上，我们的模型可以构建一种新颖的递归单元，其性能优于广泛使用的LSTM单元和其他最先进的基线模型。我们的单元在Penn Treebank上实现了62.4的测试集困惑度，比之前最先进的模型提高了3.6困惑度。该单元还可以转移到PTB上的字符语言建模任务，并实现了1.214的最先进困惑度。

1 引言

过去几年中，深度神经网络在许多具有挑战性的应用中取得了巨大成功，如语音识别（Hinton et al., 2012）、图像识别（LeCun et al., 1998; Krizhevsky et al., 2012）和机器翻译（Sutskever et al., 2014; Bahdanau et al., 2015; Wu et al., 2016）。随着这一成功，出现了一个从特征设计到架构设计的范式转变，即从SIFT（Lowe, 1999）和HOG（Dalal & Triggs, 2005）到AlexNet（Krizhevsky et al., 2012）、VGGNet（Simonyan & Zisserman, 2014）、GoogleNet（Szegedy et al., 2015）和ResNet（He et al., 2015a）。尽管设计架构变得更容易，但仍然需要大量的专家知识和时间。

本文介绍了神经架构搜索，一种基于梯度的方法，用于寻找良好的架构（见图1）。我们的工作基于以下观察：神经网络的结构和连接可以通过可变长度的字符串来指定。因此，可以使用递归网络——控制器——来生成这样的字符串。在真实数据上训练由字符串指定的网络——“子网络”——将在验证集上产生准确率。使用这个准确率作为奖励信号，我们可以计算策略梯度来更新控制器。结果是，在下一轮迭代中，控制器将给予获得高准确率的架构更高的概率。换句话说，控制器将随着时间的推移学会改进其搜索。

我们的实验表明，神经架构搜索可以从零开始设计出良好的模型，这一成就是其他方法无法实现的。在CIFAR-10上的图像识别任务中，神经架构搜索可以找到一种新颖的ConvNet模型，其性能优于大多数人类发明的架构。我们的CIFAR-10模型实现了3.65%的测试集错误率，同时比当前最佳模型快1.05倍。在Penn Treebank上的语言建模任务中，神经架构搜索可以设计一种新颖的递归单元，其性能也优于之前的RNN和LSTM架构。我们的模型发现的单元在Penn Treebank数据集上实现了62.4的测试集困惑度，比之前最先进的模型提高了3.6困惑度。

2 相关工作

超参数优化是机器学习中的一个重要研究课题，并在实践中广泛使用（Bergstra et al., 2011; Bergstra & Bengio, 2012; Snoek et al., 2012, 2015; Saxena & Verbeek, 2016）。尽管取得了成功，这些方法仍然受到限制，因为它们只能从固定长度的空间中搜索模型。换句话说，很难要求它们生成指定网络结构和连接的可变长度配置。在实践中，如果提供了一个良好的初始模型，这些方法通常效果更好（Bergstra & Bengio, 2012; Snoek et al., 2012, 2015）。有一些贝叶斯优化方法允许搜索非固定长度的架构（Bergstra et al., 2013; Mendoza et al., 2016），但它们不如本文提出的方法通用和灵活。

现代神经进化算法，例如Wierstra et al. (2005); Floreano et al. (2008); Stanley et al. (2009)，在构建新颖模型方面更加灵活，但在大规模应用中通常不太实用。它们的局限性在于它们是基于搜索的方法，因此速度较慢或需要许多启发式方法才能有效工作。

神经架构搜索与程序合成和归纳编程有一些相似之处，即从示例中搜索程序（Summers, 1977; Biermann, 1978）。在机器学习中，概率程序归纳在许多场景中成功应用，例如学习解决简单的问答（Liang et al., 2010; Neelakantan et al., 2015; Andreas et al., 2016）、对数字列表进行排序（Reed & de Freitas, 2015）以及在极少示例的情况下学习（Lake et al., 2015）。

神经架构搜索中的控制器是自回归的，这意味着它在先前预测的条件下一次预测一个超参数。这个想法借鉴了端到端序列到序列学习中的解码器（Sutskever et al., 2014）。与序列到序列学习不同，我们的方法优化了一个不可微的度量，即子网络的准确率。因此，它类似于神经机器翻译中的BLEU优化工作（Ranzato et al., 2015; Shen et al., 2016）。与这些方法不同，我们的方法直接从奖励信号中学习，没有任何监督引导。

与我们的工作相关的还有学习学习或元学习的概念（Thrun & Pratt, 2012），这是一个利用一个任务中学习到的信息来改进未来任务的通用框架。更密切相关的是使用神经网络来学习另一个网络的梯度下降更新的想法（Andrychowicz et al., 2016）以及使用强化学习为另一个网络寻找更新策略的想法（Li & Malik, 2016）。

3 方法

在以下部分中，我们将首先描述一种使用递归网络生成卷积架构的简单方法。我们将展示如何使用策略梯度方法训练递归网络，以最大化采样架构的预期准确率。我们将介绍我们核心方法的几种改进，例如形成跳跃连接以增加模型复杂性，并使用参数服务器方法加速训练。在本节的最后部分，我们将重点介绍生成递归架构，这是我们论文的另一个关键贡献。

使用控制器递归神经网络生成模型描述

在神经架构搜索中，我们使用控制器生成神经网络的架构超参数。为了灵活性，控制器被实现为递归神经网络。假设我们想要预测仅包含卷积层的卷积神经网络，我们可以使用控制器生成它们的超参数作为一系列令牌：

图2：我们的控制器递归神经网络如何采样一个简单的卷积网络。它预测一层的滤波器高度、滤波器宽度、步幅高度、步幅宽度和滤波器数量，并重复进行。每个预测都由一个softmax分类器执行，然后作为输入馈送到下一个时间步。

使用强化学习进行训练

在训练控制器时，我们使用一个计划，随着训练的进行增加子网络的层数。在CIFAR-10上，我们要求控制器每1600个样本将子网络的深度增加2层，从6层开始。

图3：神经架构搜索的分布式训练。我们使用一组S个参数服务器来存储和发送参数给K个控制器副本。每个控制器副本然后采样m个架构，并并行运行多个子模型。记录每个子模型的准确率以计算相对于θc的梯度，然后将其发送回参数服务器。

使用并行性和异步更新加速训练

在神经架构搜索中，每次梯度更新到控制器参数θcθc对应于训练一个子网络至收敛。由于训练一个子网络可能需要数小时，我们使用分布式训练和异步参数更新来加速控制器的学习过程（Dean et al., 2012）。我们使用一个参数服务器方案，其中有一个包含S个分片的参数服务器，存储K个控制器副本的共享参数。每个控制器副本采样m个不同的子架构，并并行训练。控制器然后根据该批次m个架构的收敛结果收集梯度，并将其发送给参数服务器，以更新所有控制器副本的权重。在我们的实现中，每个子网络的收敛是在其训练超过一定数量的epoch时达到的。这种并行方案如图3所示。

图4：控制器使用锚点和集合选择注意力来形成跳跃连接。

通过跳跃连接和其他层类型增加架构复杂性

在第3.1节中，搜索空间没有跳跃连接，或现代架构中使用的分支层，如GoogleNet（Szegedy et al., 2015）和Residual Net（He et al., 2015a）。在本节中，我们介绍一种方法，允许控制器提出跳跃连接或分支层，从而扩大搜索空间。

在我们的框架中，如果一层有多个输入层，则所有输入层在深度维度上连接。跳跃连接可能会导致“编译失败”，即一层与另一层不兼容，或一层可能没有任何输入或输出。为了规避这些问题，我们采用了三种简单技术。首先，如果一层没有连接到任何输入层，则使用图像作为输入层。其次，在最终层，我们将所有未连接的层输出连接起来，然后将最终隐藏状态发送到分类器。最后，如果输入层的大小不同，我们用零填充较小的层，使连接的层具有相同的大小。

最后，在第3.1节中，我们没有预测学习率，并且还假设架构仅由卷积层组成，这也是相当受限的。可以将学习率添加为预测之一。此外，还可以预测池化、局部对比度归一化（Jarrett et al., 2009; Krizhevsky et al., 2012）和批量归一化（Ioffe & Szegedy, 2015）。为了能够添加更多类型的层，我们需要在控制器RNN中添加一个额外的步骤来预测层类型，然后是与之相关的其他超参数。

图5：一个由具有两个叶节点（基数2）和一个内部节点的树构建的递归单元示例。左：定义控制器预测的计算步骤的树。中：控制器为树中每个计算步骤做出的预测示例集。右：根据控制器的示例预测构建的递归单元的计算图。

生成递归单元架构

在本节中，我们将修改上述方法以生成递归单元。在每个时间步tt，控制器需要找到一个函数形式，该函数以为输入。最简单的方法是，这是基本递归单元的公式。更复杂的公式是广泛使用的LSTM递归单元（Hochreiter & Schmidhuber, 1997）。

基本RNN和LSTM单元的计算可以概括为一系列步骤，这些步骤以为输入，并产生作为最终输出。控制器RNN需要为树中的每个节点标记一个组合方法（加法、逐元素乘法等）和一个激活函数（tanh、sigmoid等），以合并两个输入并产生一个输出。然后将两个输出作为输入馈送到树中的下一个节点。为了允许控制器RNN选择这些方法和函数，我们按顺序索引树中的节点，以便控制器RNN可以逐个访问每个节点并标记所需的超参数。

受LSTM单元构造的启发（Hochreiter & Schmidhuber, 1997），我们还需要单元变量和来表示记忆状态。为了合并这些变量，我们需要控制器RNN预测树中的哪些节点连接这两个变量。这些预测可以在控制器RNN的最后两个块中完成。

为了使这个过程更清晰，我们在图5中展示了一个示例，对于一个有两个叶节点和一个内部节点的树结构。叶节点由0和1索引，内部节点由2索引。控制器RNN需要首先预测3个块，每个块指定树中每个索引的组合方法和激活函数。之后，它需要预测最后2个块，指定如何将连接到树中的临时变量。具体来说，根据控制器RNN在这个示例中的预测，将发生以下计算步骤：

4 实验和结果

我们将我们的方法应用于CIFAR-10上的图像分类任务和Penn Treebank上的语言建模任务，这两个是深度学习中最常用的基准数据集。在CIFAR-10上，我们的目标是找到一个好的卷积架构，而在Penn Treebank上，我们的目标是找到一个好的递归单元。在每个数据集上，我们有一个单独的保留验证数据集来计算奖励信号。测试集上的报告性能仅对在保留验证数据集上取得最佳结果的网络计算一次。有关我们的实验程序和结果的更多详细信息如下。

为CIFAR-10学习卷积架构

数据集：在这些实验中，我们使用CIFAR-10数据集，并采用与其他先前结果一致的数据预处理和增强程序。我们首先通过白化所有图像来预处理数据。此外，我们对每个图像进行上采样，然后选择该上采样图像的随机32x32裁剪。最后，我们对这个32x32裁剪图像使用随机水平翻转。

搜索空间：我们的搜索空间由卷积架构组成，使用修正线性单元作为非线性（Nair & Hinton, 2010），批量归一化（Ioffe & Szegedy, 2015）和层之间的跳跃连接（第3.3节）。对于每个卷积层，控制器RNN需要选择滤波器高度在[1, 3, 5, 7]中，滤波器宽度在[1, 3, 5, 7]中，滤波器数量在[24, 36, 48, 64]中。对于步幅，我们进行两组实验，一组固定步幅为1，另一组允许控制器预测步幅在[1, 2, 3]中。

训练细节：控制器RNN是一个两层LSTM，每层有35个隐藏单元。它使用Adam优化器（Kingma & Ba, 2015）进行训练，学习率为0.0006。控制器的权重在-0.08和0.08之间均匀初始化。对于分布式训练，我们将参数服务器分片数S设置为20，控制器副本数K设置为100，子副本数m设置为8，这意味着在任何时候都有800个网络在800个GPU上并行训练。

一旦控制器RNN采样一个架构，就会构建并训练一个子模型50个epoch。用于更新控制器的奖励是最后5个epoch的最大验证准确率的立方。验证集有5000个随机采样的示例，剩余的45000个示例用于训练。训练CIFAR-10子模型的设置与Huang et al. (2016c)中使用的设置相同。我们使用动量优化器，学习率为0.1，权重衰减为1e-4，动量为0.9，并使用Nesterov动量（Sutskever et al., 2013）。

结果：在控制器训练了12800个架构后，我们找到了实现最佳验证准确率的架构。然后我们对学习率、权重衰减、批量归一化epsilon和学习率衰减的epoch进行小网格搜索。从该网格搜索中找到的最佳模型运行至收敛，然后计算该模型的测试准确率，并在表1中总结结果。从表中可以看出，神经架构搜索可以设计出几个有前途的架构，其性能与该数据集上的一些最佳模型相当。

首先，如果我们要求控制器不预测步幅或池化，它可以设计一个15层的架构，在测试集上实现5.50%的错误率。这个架构在准确率和深度之间有很好的平衡。事实上，它是表中性能最好的网络中最浅且可能最便宜的架构。该架构如图7所示。该架构的一个显著特点是它有许多矩形滤波器，并且在顶层更喜欢较大的滤波器。与残差网络（He et al., 2015a）类似，该架构也有许多一步跳跃连接。这个架构是一个局部最优，因为如果我们扰动它，其性能会变得更差。例如，如果我们密集连接所有层与跳跃连接，其性能会略微变差：5.56%。如果我们移除所有跳跃连接，其性能下降到7.97%。

在第二组实验中，我们要求控制器在预测其他超参数的同时预测步幅。如前所述，这更具挑战性，因为搜索空间更大。在这种情况下，它找到一个20层的架构，在测试集上实现6.01%的错误率，这与第一组实验的结果相差不大。

最后，如果我们允许控制器在架构的第13层和第24层包含2个池化层，控制器可以设计一个39层的网络，实现4.47%的错误率，这与实现3.74%的最佳人类发明架构非常接近。为了限制搜索空间的复杂性，我们的模型预测13层，其中每层预测是一个由3层组成的完整块。此外，我们将模型可以预测的滤波器数量从[24, 36, 48, 64]更改为[6, 12, 24, 36]。通过为我们的架构的每一层添加40个滤波器，我们的结果可以提高到3.65%。此外，这个添加了40个滤波器的模型比实现3.74%的DenseNet模型快1.05倍，同时性能更好。实现3.46%错误率的DenseNet模型（Huang et al., 2016a）使用1x1卷积来减少其总参数数量，我们没有这样做，因此这不是一个精确的比较。

为Penn Treebank学习递归单元

数据集：我们将神经架构搜索应用于Penn Treebank数据集，这是一个著名的语言建模基准。在这个任务中，LSTM架构往往表现出色（Zaremba et al., 2014; Gal, 2015），改进它们很困难（Jozefowicz et al., 2015）。由于PTB是一个小数据集，需要正则化方法来避免过拟合。首先，我们使用Zaremba et al. (2014)和Gal (2015)中提出的嵌入dropout和递归dropout技术。我们还尝试将它们与输入和输出嵌入共享的方法结合，例如Bengio et al. (2003); Mnih & Hinton (2007)，特别是Inan et al. (2016)和Press & Wolf (2016)。使用这种方法的结果标记为“共享嵌入”。

搜索空间：根据第3.4节，我们的控制器依次为树中的每个节点预测一个组合方法和一个激活函数。对于树中的每个节点，控制器RNN需要选择组合方法在[add, elem_mult]中，激活方法在[identity, tanh, sigmoid, relu]中。输入对的数量称为“基数”，在我们的实验中设置为8。当基数为8时，搜索空间大约有个架构，这比我们允许控制器评估的15000个架构大得多。

训练细节：控制器及其训练几乎与CIFAR-10实验相同，除了几个修改：1）控制器RNN的学习率为0.0005，略小于CIFAR-10中的控制器RNN，2）在分布式训练中，我们将S设置为20，K设置为400，mm设置为1，这意味着在任何时候都有400个网络在400个CPU上并行训练，3）在异步训练中，我们只在从副本累积了10个梯度后才进行参数服务器更新。

在我们的实验中，每个子模型构建并训练35个epoch。每个子模型有两层，隐藏单元的数量调整，使得可学习参数的总数大约与“中等”基线（Zaremba et al., 2014; Gal, 2015）匹配。在这些实验中，我们只让控制器预测RNN单元结构，并固定所有其他超参数。奖励函数是，其中c是一个常数，通常设置为80。

在控制器RNN完成训练后，我们根据最低验证困惑度选择最佳RNN单元，然后对学习率、权重初始化、dropout率和衰减epoch进行网格搜索。找到的最佳单元随后以三种不同的配置和大小运行，以增加其容量。

结果：在表2中，我们提供了PTB数据集上架构及其性能的综合列表。从表中可以看出，神经架构搜索发现的模型在该数据集上优于其他最先进的模型，我们最好的模型实现了几乎3.6困惑度的提升。不仅我们的单元更好，实现64困惑度的模型也比之前的最佳网络快两倍以上，因为之前的最佳网络每时间步需要运行单元10次（Zilly et al., 2016）。

新发现的单元在附录A的图8中可视化。可视化显示，新单元在最初几步与LSTM单元有许多相似之处，例如它喜欢多次计算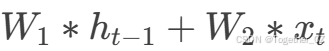，并将它们发送到单元的不同组件。

迁移学习结果：为了了解单元是否可以推广到不同任务，我们将其应用于同一数据集上的字符语言建模任务。我们使用与Ha et al. (2016)类似的实验设置，但使用Gal (2015)的变分dropout。我们还使用我们的设置训练我们自己的LSTM，以获得公平的LSTM基线。模型训练80K步，根据验证集困惑度最佳的步骤选择最佳测试集困惑度。我们的方法和最先进方法在测试集上的结果如表3所示。在小设置（5-6M参数）上的结果确认新单元确实可以推广，并且优于LSTM单元。

表2：Penn Treebank语言建模任务测试集上的单模型困惑度。带有‡的参数数量是根据Merity et al. (2016)的估计。

表3：我们的单元与PTB字符建模上最先进方法的比较。新单元是在词级语言建模上发现的。

此外，我们还进行了一个更大的实验，模型有16.28M参数。该模型权重衰减率为1e-4，训练600K步（比上述模型更长），测试困惑度取验证集困惑度最高时的值。我们使用Gal (2015)中描述的dropout率0.2和0.5，但不使用嵌入dropout。我们使用学习率为0.001的Adam优化器和128的输入嵌入大小。我们的模型有两层，每层有800个隐藏单元。我们使用32的批量大小和100的BPTT长度。在这个设置下，我们的模型实现了1.214的困惑度，这是该任务的新最先进结果。

最后，我们还将我们的单元放入之前为LSTM单元调优的GNMT框架（Wu et al., 2016）中，并训练一个WMT14英语→德语翻译模型。GNMT网络在编码器中有8层，在解码器中有8层。编码器的第一层有双向连接。注意力模块是一个具有1个隐藏层的神经网络。当使用LSTM单元时，每层的隐藏单元数为1024。模型在分布式设置中训练，有一个参数服务器和12个工作节点。此外，每个工作节点使用8个GPU和128的批量大小。我们使用学习率为0.0002的Adam在前60K训练步骤中，然后使用学习率为0.5的SGD直到400K步。之后，学习率每100K步除以2，直到达到0.1。训练在800K步停止。更多细节可以在Wu et al. (2016)中找到。

在我们的新单元实验中，除了放入新单元并调整超参数以使新模型与基模型具有相同的计算复杂度外，我们对上述设置不做任何更改。结果显示，我们的单元在相同的计算复杂度下，比默认的LSTM单元提高了0.5测试集BLEU。尽管这一改进不大，但新单元可以在现有GNMT框架中使用而无需任何调优，这一点令人鼓舞。我们期望进一步调优可以帮助我们的单元表现更好。

控制实验1 - 在搜索空间中添加更多函数：为了测试神经架构搜索的鲁棒性，我们在组合函数列表中添加了max，在激活函数列表中添加了sin，并重新运行我们的实验。结果显示，即使搜索空间更大，模型也能实现可比性能。带有max和sin的最佳架构如图8所示。

控制实验2 - 与随机搜索的比较：除了策略梯度，还可以使用随机搜索来找到最佳网络。尽管这个基线看起来简单，但它通常很难超越（Bergstra & Bengio, 2012）。我们在图6中报告了使用策略梯度相对于随机搜索的困惑度改进随时间的变化。结果显示，不仅使用策略梯度的最佳模型优于使用随机搜索的最佳模型，而且前k个模型的平均值也更好。

图6：神经架构搜索随时间对随机搜索的改进。我们绘制了每运行400个模型时，控制器找到的前k个模型的平均值与随机搜索之间的差异。

5 结论

在本文中，我们介绍了神经架构搜索，一种使用递归神经网络构建神经网络架构的想法。通过使用递归网络作为控制器，我们的方法具有灵活性，可以搜索可变长度的架构空间。我们的方法在非常具有挑战性的基准上具有强大的实证性能，并为自动寻找良好的神经网络架构提出了一个新的研究方向。运行控制器在CIFAR-10和PTB上发现的模型的代码将在https://github.com/tensorflow/models上发布。此外，我们使用我们的方法发现的RNN单元已命名为NASCell并添加到TensorFlow中，以便其他人可以轻松使用它。

致谢：我们感谢Greg Corrado、Jeff Dean、David Ha、Lukasz Kaiser和Google Brain团队对项目的帮助。