神经网络与BP算法推导

导言

神经网络是深度学习基础，BP算法是神经网络训练中最基础的算法。因此，对神经网络结构和BP算法进行梳理是理解深度学习的有效方法。参考资料UFLDL，BP推导，神经网络教材。

神经网络结构

典型网络为浅层网络，一般2~4层。其结构如下图所示：

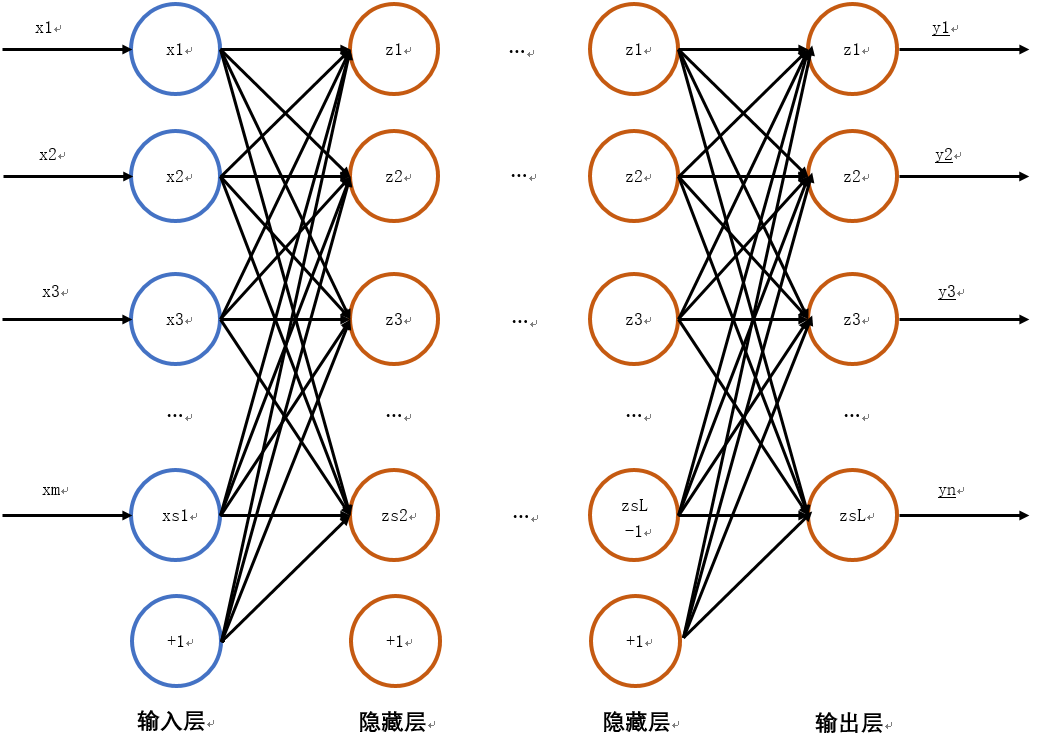
假设神经网络有L层，第$1$层为输入层，最后一层（第$L$层）为输出层，中间$2，3，……L-1$为隐层。每层有$S_{l},l=1,2,......L$个节点，$+1$节点用来表示偏置（bias）；$b_{i}^{(l)}$表示第$l$层的$+1$节点与第$l+1$层的第$i$个节点连接上的权（偏置）。每一层的节点与上一层连接（不一定全连接），连接权重$W_{ij}^{(l)}$表示层$l$上的节点$j$同层$l+1$的节点$i$之间的权重。训练集包含$K$组输入和输出样本，$\{(\vec{x_{1}},\vec{y_{1}}),(\vec{x_{2}},\vec{y_{2}}),\dots, (\vec{x_{K}},\vec{y_{K}})\}$。其中$(\vec{x_{k}},\vec{y_{k}}), k=1,2,3,\dots,K$为向量组：

$$\vec{x_{k}}=\{ x_{1},x_{2},\dots, x_{i},\dots, x_{m} \}$$

$$\vec{y_{k}}=\{y_{1},y_{2},\dots, y_{j},\dots, y_{n}\}$$
用 $z$表示对上一层输出的权重和汇集结果，由网络结构可以知输入层到第一个隐层：
$$\begin{align} z_{1}^{(2)} & = W_{11}^{(1)}*x_{1}+W_{12}^{(1)}*x_{2}+\dots+W_{1m}^{(1)}*x_{m}+b_{1}^{(1)} \\ z_{2}^{(2)} & = W_{21}^{(1)}*x_{1}+W_{22}^{(1)}*x_{2}+\dots+W_{2m}^{(1)}*x_{m}+b_{2}^{(1)} \\ z_{3}^{(2)} & = W_{31}^{(1)}*x_{1}+W_{32}^{(1)}*x_{2}+\dots+W_{3m}^{(1)}*x_{m}+b_{3}^{(1)} \\ \dots &= \dots\\ z_{S_{2}}^{(2)} & = W_{S_{2}1}^{(1)}*x_{1}+W_{S_{2}2}^{(1)}*x_{2}+\dots+W_{S_{2}m}^{(1)}*x_{m}+b_{S_{2}}^{(1)} \end{align}$$
在之后各层的算法类似，只是将输入换做层 $l$的输出即可。我们用$h$表示加权和 $z$经过非线性激活函数得到输出 $h_{i}^{(l)}=f(z_{i}^{(l)})，f$为sigmoid函数或者tanh（双正切）函数。
$$\begin{align}z_{1}^{(l+1)} & = W_{11}^{(l)}*h_{1}^{(l)}+W_{12}^{(l)}*h_{2}^{(l)}+\dots+W_{1S_{l}}^{(l)}*h_{S_{l}}^{(l)}+b_{1}^{(l)} \\ z_{2}^{(l+1)} & = W_{21}^{(l)}*h_{1}^{(l)}+W_{22}^{(l)}*h_{2}^{(l)}+\dots+W_{2S_{l}}^{(l)}*h_{S_{l}}^{(l)}+b_{2}^{(l)} \\ z_{3}^{(l+1)} & = W_{31}^{(l)}*h_{1}^{(l)}+W_{32}^{(l)}*h_{2}^{(l)}+\dots+W_{3S_{l}}^{(l)}*h_{S_{l}}^{(l)}+b_{3}^{(l)} \\ \dots &= \dots\\ z_{S_{l+1}}^{(l+1)} & = W_{S_{l+1}1}^{(l)}*h_{1}^{(l)}+W_{S_{l+1}2}^{(l)}*h_{2}^{(l)}+\dots+W_{S_{l+1}S_{l}}^{(l)}*h_{S_{l}}^{(l)}+b_{S_{l+1}}^{(l)} \end{align} \qquad (1)$$
我们令 $h_{i}^{(1)} = x_{i}, i=1,2,\dots,S_{1}$; $h_{i}^{(L)} = f(z_{i}^{(L)})$ 就可以将所有的层统一成如下形式:
$$\begin{align}h_{1}^{(l+1)} & = f(W_{11}^{(l)}*h_{1}^{(l)}+W_{12}^{(l)}*h_{2}^{(l)}+\dots+W_{1S_{l}}^{(l)}*h_{S_{l}}^{(l)}+b_{1}^{(l)}) \\ h_{2}^{(l+1)} & = f(W_{21}^{(l)}*h_{1}^{(l)}+W_{22}^{(l)}*h_{2}^{(l)}+\dots+W_{2S_{l}}^{(l)}*h_{S_{l}}^{(l)}+b_{2}^{(l)}) \\ h_{3}^{(l+1)} & = f(W_{31}^{(l)}*h_{1}^{(l)}+W_{32}^{(l)}*h_{2}^{(l)}+\dots+W_{3S_{l}}^{(l)}*h_{S_{l}}^{(l)}+b_{3}^{(l)} )\\ \dots &= \dots\\ h_{S_{l+1}}^{(l+1)} & = f(W_{S_{l+1}1}^{(l)}*h_{1}^{(l)}+W_{S_{l+1}2}^{(l)}*h_{2}^{(l)}+\dots+W_{S_{l+1}S_{l}}^{(l)}*h_{S_{l}}^{(l)}+b_{S_{l+1}}^{(l)}) \\ \end{align} \qquad (2)$$
上述公式中 $l=1,2,\dots,L-1$，每一层的输出值也可以写为向量形式：
$$\vec{h^{(l)}}=\{ h_{1}^{(l)},h_{2}^{(l)},\dots,h_{S_{l}}^{(l)} \}$$
则公式（2）改写为矩阵向量形式，该公式用于前向传播：
$$\begin{align} \vec{z^{(l+1)}}&=W^{(l)}\vec{h^{(l)}}+\vec{b^{(l)}}\\ \vec{h^{(l+1)}}&=f(\vec{z^{(l+1)}})\\ \end{align}$$
其中，每个节点有如下形式：
$$\begin{align} z^{(l+1)}_{i}&=\sum_{j=1} ^{S_{l}}W^{(l)}_{ij}h^{(l)}_{j}+b^{(l)}_{i}\\ h^{(l+1)}_{i}&=f(z^{(l+1)}_{i})\\ \end{align}$$

神经网络激活函数

激活函数是非线性函数，常用的有两种：sigmoid函数和tanh函数，其导数形式简单。

$$\begin{align} sigmoid: f(x)&=\frac{1}{1+e^{-x}}\\ tanh: f(x)&=\frac{1-e^{-x}}{1+e^{-x}}\\ \end{align}$$
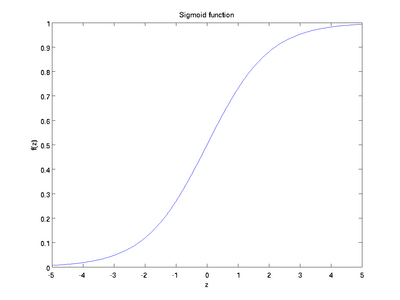
$sigmod$函数的图像如下图所示，它的变化范围为(0, 1)，其导数为 $f′=f(1−f)$

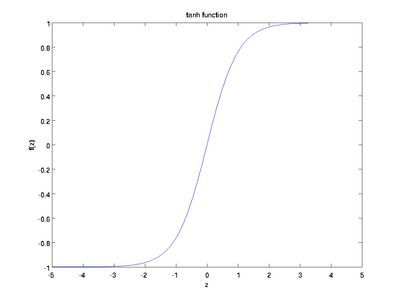
$tanh$函数的图像如下图所示，它的变化范围为(-1, 1)，其导数为 $f′=1−f^{2}$

BP算法推导

训练的损失函数采用的是均方差最小化为指标，因此其损失函数为:

$$J(W,d;x,y)=\frac{1}{2}||h_{Wb}(x)-y||^2$$
真正训练时往往采用分批次（in batches）学习（批量随机梯度下降法），假设样本集中每次取 $T$个样本进行训练，则整体的损失函数为：
$$\begin{align} J(W,b)&=\left[\frac{1}{T}\sum_{t=1}^{T}J(W,b;x^t,y^t)\right]+\frac{\lambda}{2}\sum_{l=1}^{L-1} \sum_{j=1}^{S_{l}} \sum_{i=1}^{S_{l+1}}(W_{ij}^{(l)})^2\\ &=\left[\frac{1}{T}\sum_{t=1}^{B}\left(\frac{1}{2}||h_{Wb}(x^t)-y^t||^2\right)\right]+\frac{\lambda}{2}\sum_{l=1}^{L-1} \sum_{j=1}^{S_{l}} \sum_{i=1}^{S_{l+1}}(W_{ij}^{(l)})^2 \end{align}$$
以上公式中J(W,b)的第一项是均方差项( $T$个样本的均值);第二项是一个规则化项（也叫权重衰减项 weight decay），其目的是减小权重的幅度，防止过度拟合。

梯度更新规则

随机梯度下降法每次迭代将对权重和偏置进行更新，更新规则如下：

$$\begin{align} W_{ij}^{(l)} &= W_{ij}^{(l)} -\alpha \frac{\partial }{\partial W_{ij}^{(l)}}J(W,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} -\alpha \frac{\partial }{\partial b_{i}^{(l)}}J(W,b) \end{align}$$
其中 $\alpha$为学习率（learning rate），关键步骤是计算偏导数。我们对 $W_{ij}^{(l)}$和 $b_{i}^{(l)}$计算偏导数如下：
$$\begin{align} \frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)&=\left[\frac{1}{T}\sum_{t=1}^{T}\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b;x^t,y^t)\right]+\lambda W_{ij}^{(l)} \\ \frac{\partial }{\partial b_{i}^{(l)}}J(W,b)&=\left[\frac{1}{T}\sum_{t=1}^{T}\frac{\partial }{\partial b_{i}^{(l)}}J(W,b;x^t,y^t)\right] \end{align}$$
由上式可知，需要求单个样本的偏导数，带入求批量的偏导，然后使用更新公式进行权重的更新，下面求单个样本的偏导：

1. 样本向量$\vec{x^{(t)}}$输入经过前向传播传到输出层，得到输出向量，其每个节点的计算如式(3)所示$\vec{h^{(L)}}=\vec{h_{Wb}}(x^t)=\{ h_{1}^{(L)},h_{2}^{(L)},\dots,h_{S_{L}}^{(L)} \}, 其中S_{L}=n$为输出层节点个数
   

   $$\begin{align} h_{i}^{(L)}&= f(z_{(i)}^{(L)}) \\ &=f(W_{i1}^{(L-1)}*h_{1}^{(L-1)}+W_{i2}^{(L-1)}*h_{2}^{(L-1)}+\dots+W_{iS_{L-1}}^{(L-1)}*h_{S_{L-1}}^{(L-1)}+b_{i}^{(L-1)}) \qquad (3) \\ &= f\left( \sum_{j=1}^{S_{L-1}}W_{ij}^{L-1}*h_{j}^{L-1} +b_{i}^{(L-1)} \right) \end{align}$$

2. 对于输出层$L$，每个节点$h_{i}^{(L)}$与样本t的标签之第$i$个分量$y_{i}^t$进行比较。带入单个样本的损失函数中得：
   

   $$\begin{align} J(W,d;x^t,y^t)&=\frac{1}{2}||\vec{h_{Wb}}(x^t)-\vec{y^t}||^2\\ &=\frac{1}{2}\sum_{i=1}^{S_{L}}(h_{i}^{(L)}-y_{i}^t)^2\\ &=\frac{1}{2}\sum_{i=1}^{S_{L}}(f(z_{(i)}^{(L)})-y_{i}^t)^2\\ &=\frac{1}{2}\sum_{i=1}^{S_{L}}\left(f\left( \sum_{j=1}^{S_{L-1}}W_{ij}^{L-1}*h_{j}^{L-1} +b_{i}^{(L-1)} \right)-y_{i}^t\right)^2 \end{align} \qquad (4)$$

3. 对网络的输出层$L$，根据链式求导法则，对公式(4)求偏导，得到公式(5)
   $$\begin{align} \frac{\partial }{\partial W_{ij}^{(L-1)}}J(W,b;x^t,y^t) &=\frac{1}{2}*2*(f(z_{(i)}^{(L)})-y_{i}^t) * \frac{\partial f(z_{(i)}^{(L)})}{\partial W_{ij}^{(L-1)}} \\ &=(f(z_{(i)}^{(L)})-y_{i}^t)*f'(u)|_{u=z_{(i)}^{(L)}}*\frac{\partial z_{(i)}^{(L)}}{\partial W_{ij}^{(L-1)}} \\ &=(f(z_{(i)}^{(L)})-y_{i}^t)*f'(u)|_{u=z_{(i)}^{(L)}}*h_{j}^{L-1}\\ &=(h_{i}^{(L)}-y_{i}^t)*f'(u)|_{u=z_{(i)}^{(L)}}*h_{j}^{L-1} \end{align} \qquad (5)$$

$$\begin{align} \frac{\partial }{\partial b_{i}^{(L-1)}}J(W,b;x^t,y^t) &=\frac{1}{2}*2*(f(z_{(i)}^{(L)})-y_{i}^t) * \frac{\partial f(z_{(i)}^{(L)})}{\partial b_{i}^{(L-1)}} \\ &=(f(z_{(i)}^{(L)})-y_{i}^t)*f'(u)|_{u=z_{(i)}^{(L)}}*\frac{\partial z_{(i)}^{(L)}}{\partial b_{i}^{(L-1)}} \\ &=(f(z_{(i)}^{(L)})-y_{i}^t)*f'(u)|_{u=z_{(i)}^{(L)}}*1\\ &=(h_{i}^{(L)}-y_{i}^t)*f'(u)|_{u=z_{(i)}^{(L)}} \end{align} \qquad (6)$$
令 $\delta_{i}^{L}=(h_{i}^{(L)}-y_{i}^t)*f'(u)|_{u=z_{(i)}^{(L)}}$表示第 $L$层中节点$i$的残差，则公式(5)(6)可以写做:
$$\begin{align} \frac{\partial }{\partial W_{ij}^{(L-1)}}J(W,b;x^t,y^t) &=\delta_{i}^{L}*h_{j}^{L-1}\\ \frac{\partial }{\partial b_{i}^{(L-1)}}J(W,b;x^t,y^t) &=\delta_{i}^{L} \end{align}$$
4. 对于隐藏层 $L-1$，根据前向传播法则展开至 $W_{ij}^{(L-2)}$同样按链式法则求导，可得式(7)，(8)
$$\begin{align} \frac{1}{2} ||\vec{h_{Wb}}(x^t)-\vec{y^t}||^2&=\frac{1}{2}\sum_{k=1}^{S_{L}}(h_{k}^{(L)}-y_{k}^t)^2\\ &= \frac{1}{2}\sum_{k=1}^{S_{L}}(f(z_{(k)}^{(L)})-y_{k}^t)^2\\ &= \frac{1}{2}\sum_{k=1}^{S_{L}}\left(f\left( \sum_{i=1}^{S_{L-1}}W_{ki}^{(L-1)}*h_{i}^{(L-1)} +b_{k}^{(L-1)} \right)-y_{k}^t\right)^2\\ &= \frac{1}{2}\sum_{k=1}^{S_{L}}\left(f\left( \sum_{i=1}^{S_{L-1}}W_{ki}^{(L-1)}*f(z_{i}^{(L-1)}) +b_{k}^{(L-1)} \right)-y_{k}^t\right)^2\\ &= \frac{1}{2}\sum_{k=1}^{S_{L}}\left(f\left( \sum_{i=1}^{S_{L-1}}W_{ki}^{(L-1)}* f\left( \sum_{j=1}^{S_{L-2}}W_{ij}^{(L-2)}*h_{j}^{(L-2)} +b_{i}^{(L-2)} \right) +b_{k}^{(L-1)} \right)-y_{k}^t\right)^2 \end{align}$$

$$\begin{align} \frac{\partial J(W,b;x^t,y^t)}{\partial W_{ij}^{(L-2)}} &=\frac{\partial }{\partial W_{ij}^{(L-2)}} \left(\frac{1}{2}||\vec{h_{Wb}}(x^t)-\vec{y^t}||^2\right) \\ &= \frac{\partial }{\partial W_{ij}^{(L-2)}} \left(\frac{1}{2}\sum_{k=1}^{S_{L}}(h_{k}^{(L)}-y_{k}^t)^2 \right)\\ &= \frac{\partial }{\partial W_{ij}^{(L-2)}} \left(\frac{1}{2}\sum_{k=1}^{S_{L}}(f(z_{(k)}^{(L)})-y_{k}^t)^2 \right)\\ &=\sum_{k=1}^{S_{L}}(h_{k}^{(L)}-y_{k}^t)*f'(u)|_{u=z_{(k)}^{(L)}}*\frac{\partial (z_{(k)}^{(L)})}{\partial W_{ij}^{(L-2)}} \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*\frac{\partial }{\partial W_{ij}^{(L-2)}} \left( \sum_{i=1}^{S_{L-1}}W_{ki}^{(L-1)}*h_{i}^{(L-1)} +b_{k}^{(L-1)} \right) \qquad (7) \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*\frac{\partial (h_{i}^{(L-1)}) }{\partial W_{ij}^{(L-2)}} \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*\frac{\partial }{\partial W_{ij}^{(L-2)}} f(z_{i}^{(L-1)}) \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*\frac{\partial }{\partial W_{ij}^{(L-2)}} f\left( \sum_{j=1}^{S_{L-2}}W_{ij}^{(L-2)}*h_{j}^{(L-2)} +b_{i}^{(L-2)} \right) \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*f'(v)|_{v=z_{i}^{(L-1)}}*h_{j}^{(L-2)} \\ \end{align}$$

$$\begin{align} \frac{\partial J(W,b;x^t,y^t)}{\partial b_{i}^{(L-2)}} &=\frac{\partial }{\partial b_{i}^{(L-2)}} \left(\frac{1}{2}||\vec{h_{Wb}}(x^t)-\vec{y^t}||^2\right) \\ &= \frac{\partial }{\partial b_{i}^{(L-2)}} \left(\frac{1}{2}\sum_{k=1}^{S_{L}}(h_{k}^{(L)}-y_{k}^t)^2 \right)\\ &= \frac{\partial }{\partial b_{i}^{(L-2)}} \left(\frac{1}{2}\sum_{k=1}^{S_{L}}(f(z_{(k)}^{(L)})-y_{k}^t)^2 \right)\\ &=\sum_{k=1}^{S_{L}}(h_{k}^{(L)}-y_{k}^t)*f'(u)|_{u=z_{(k)}^{(L)}}*\frac{\partial (z_{(k)}^{(L)})}{\partial b_{i}^{(L-2)}} \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*\frac{\partial }{\partial b_{i}^{(L-2)}} \left( \sum_{i=1}^{S_{L-1}}W_{ki}^{(L-1)}*h_{i}^{(L-1)} +b_{k}^{(L-1)} \right)\\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*\frac{\partial (h_{i}^{(L-1)}) }{\partial b_{i}^{(L-2)}} \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*\frac{\partial }{\partial b_{i}^{(L-2)}} f(z_{i}^{(L-1)}) \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*\frac{\partial }{\partial b_{i}^{(L-2)}} f\left( \sum_{j=1}^{S_{L-2}}W_{ij}^{(L-2)}*h_{j}^{(L-2)} +b_{i}^{(L-2)} \right) \\ &=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*f'(v)|_{v=z_{i}^{(L-1)}}*1\\ \end{align} \qquad (8)$$
令：
$$\delta_{i}^{(L-1)}=\sum_{k=1}^{S_{L}} \delta_{k}^{L}*W_{ki}^{(L-1)}*f'(v)|_{v=z_{i}^{(l)}}$$

可以看出残差$\delta_{i}^{(L-1)}$相当于残差$\delta_{k}^{L}$反向传播一层后乘以非线性激活函数在$L-1$层该节点的导数值，故(7)(8)式可改写为：

$$\begin{align} \frac{\partial J(W,b;x^t,y^t)}{\partial W_{ij}^{(L-2)}} &= \delta_{i}^{(L-1)}*h_{j}^{(L-2)}\\ \frac{\partial J(W,b;x^t,y^t)}{\partial b_{i}^{(L-2)}} &= \delta_{i}^{(L-1)} \end{align}$$

1. 同理可得其他隐层的递推公式，对任意隐层$l=1,2,3,\dots,L-1$,单样本损失函数对权重和偏置的偏导的计算公式如(9)，其中残差从输出层反向传播到层$l$：
   $$\begin{align} \frac{\partial J(W,b;x^t,y^t)}{\partial W_{ij}^{(l)}} &= \delta_{i}^{(l+1)}*h_{j}^{(l)}\\ \frac{\partial J(W,b;x^t,y^t)}{\partial b_{i}^{(l)}} &= \delta_{i}^{(l+1)} \end{align} \qquad (9)$$
   其中：
   $$\delta_{i}^{(l)}=\sum_{k=1}^{S_{l+1}} \delta_{k}^{l+1}*W_{ki}^{(l)}*f'(v)|_{v=z_{i}^{(l)}}$$

BP算法的批量更新步骤如下：

1. 对所有的层$1≤l≤L-1$，$\nabla W^{(l)}$与$\nabla b^{(l)}$初始化为0，用以记录批量累计误差；
2. for t = 1: T
   每个样本正向计算各层输出
   使用反向传播算法，计算各层神经元权值和偏置的梯度矩阵$\nabla W^{(l)}(t)$与$\nabla b^{(l)}(t)$
   累积误差：
   $$\begin{align} \nabla W^{(l)}&+= \nabla W^{(l)}(t)\\ \nabla b^{(l)}&+= \nabla b^{(l)}(t) \end{align}$$
   end for
3. 更新权重与偏置
   $$\begin{align} W^{(l)}&= W^{(l)}+\frac{1}{T}\nabla W^{(l)}+\lambda W^{(l)}\\ b^{(l)}&= b^{(l)}+\frac{1}{T}\nabla b^{(l)} \end{align}$$