微积分笔记（一）--预备知识

预备知识

什么是微积分

微积分（Calculus）是研究函数的微分、积分以及有关概念和应用的数学分支。它是数学的一个基础学科。内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。

预备知识主要复习在开始学习微积分时要知道的最重要的知识，重点是函数和图形。

一、 直线

证明微积分是如此有用的一个理由在于微积分是把一个量的变化率和该量的图形联系起来的正确的数学，解释这种关系要从直线的斜率开始。

1.1 增量

定义：如果一个质点从点(x₁,y₁)，移动到点(x₂,y₂)，其坐标的增量为

∆x = x₂ - x₁ 和 ∆y = y₂ - y₁ .

增量可以是正的、负的或零。记号 ∆ 读作 “delta”。

1.2 直线的斜率

每条非垂直的直线l，有一个斜率，每行进单位距离时高度的变化称为直线的斜率。

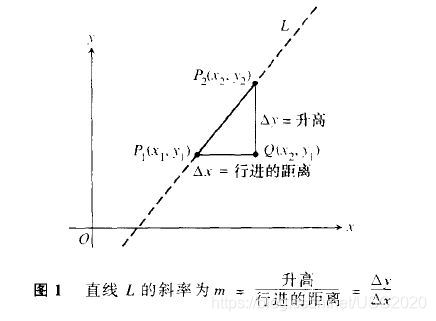
我们称 ∆y = y₂ - y₁ 为 P₁ 到 P₂ 的升高，∆x = x₂ - x₁ 是从 P₁ 到 P₂ 行进的距离。

定义：设 P₁ (x₁,y₁) 和 P₂ (x₂,y₂) 是非垂直直线 L 上的两个点。L的斜率为
$$m=\frac{升高}{行进的距离}=\frac{∆y}{∆x}=\frac{y₂-y₁}{x₂-x₁}$$
当x增加时上升的直线具有正斜率；当x增加时下降的直线具有负斜率。水平线的斜率为零，因为其上的点具有相同的 y 坐标，使得 ∆y = 0.对垂直的直线，∆x = 0，从而 ∆y/∆x 是无意义的，我们说垂直直线没有斜率来表示这一事实。

1.3 平行线和垂直线

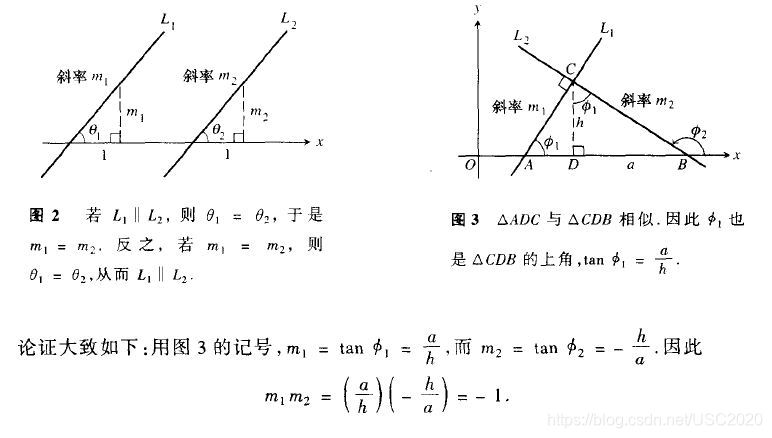
平行线与x轴的夹角相等（图a）。因此，非垂直的平行线具有相同的斜率。反之，具有相同斜率的直线与x轴的交角相等，所以是平行线。

如果两条非垂直直线 L₁ 和 L₂ 是相互垂直的，其斜率 m₁ 和 m₂ 满足m₁m₂ = -1，所以每个斜率是另一个斜率的负倒数：
$$m₁=-\frac{1}{m}₂,m₂=-\frac{1}{m}₁$$

1.4 直线的方程

如果我们知道直线的斜率m和直线上的一点P₁(x₁,y₁)，我们可以写出任何非垂直线的方程。因为如果P(x,y)是直线上任意一点，则
$$\frac{y-y₁}{x-x₁}=m$$
所以
$$y-y₁=m(x-x₁)或y=m(x-x₁)+y₁.$$
点 - 斜式方程

定义：方程
y = m ( x −