排列组合

最新推荐文章于 2025-03-13 15:50:14 发布

瓦特what？

最新推荐文章于 2025-03-13 15:50:14 发布

阅读量2k

点赞数 40

文章标签：算法

本文链接：https://blog.csdn.net/Uk110/article/details/145064383

版权

排列组合概念：

排列组合是组合学最基本的概念

排列:就是指从给定个数的元素中取出指定个数的元素进行排序。组合:则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。

列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。

加法原理和乘法原理
        加法原理: 做一件事情,完成它可以有 n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法,以此类推，在第n类办法中有 mn种不同的方法。那么完成这件事共有 N=m1+m2+..+mn种不同的方法。
        乘法原理: 做一件事情,完成它需要分成 n个步骤，做第一步有m1种不同的方法做第二步有m2种不同的方法,以此类推,做第 n 步有mn种不同的方法,那么完成这件事有 N=m1*m2*m3*...*mn种不同的方法。
        两个原理的区别是:一个与分类有关,一个与分步有关;加法原理是“分类完成”乘法原理是“分步完成”

                加法原理
                        即完成一件事情，需要划分几个类别，各类别中的方法可以独立完成这件事情。当这种分类没有重复、没有遗漏时，完成这件事情的方法总数等于每一类方法数之和。
                        【举例说明】从A地到B地，有3个车次的火车，有5趟汽车，2班飞机。那么从A地到B地一共有3+5+2=10种方法。

                乘法原理
                        即完成一件事情，需要分为几个步骤，每个步骤内的方法刚好完成该步骤，所有步骤实施完毕刚好完成这件事，则完成这件事情的方法总数等于每一个步骤的方法数之积。
                        【举例说明】从A地到B地需在C地转机，已知从A地到C地有4种方法从C地到B地有3种方法。那么从A地到B地要分两步，A→C、C→B，共有4x3=12种方法。

课堂练习1
甲班有10人，乙班有8人，丙班有5人，各选出一人当班代，请有几种不同的结果?//答案评论区

排列
排列: 从 n个不同元素中任取 m(m<=n)个元素,按照一定的顺序排成一列,称为从n 个不同元素中取出 m 个元素的一个排列。 排列数: 从n 个不同元素中取出 m(m<=n)个元素的所有排列的个数,称为从n个不同元素中取出 m 个元素的排列数,用符 $A^{_{n}^{m}}$ 表示。排列数的计算公式为

组合
组合: 从 n个不同元素中任取 m(m<=n)个元素合并成一组,称为从 n个不同元素中取出 m 个元素的一个组合。组合数:从 n个不同元素中取出 m(m<=n)个元素的所有组合的个数称为从 n个不同元素中取出 m 个元素的组合数,用符号 $C^{_{n}^{m}}$ 表示。组合数的计算公式为

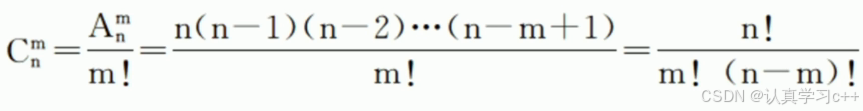
排列组合公式：

课堂练习2
5个人排成一列，有几种不同的排法?//答案评论区

课堂练习3
某人班级有10人，要选出两个人担任值日生，几种选法?//答案评论区

容斥原理
在计数时，必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出了一种新的计数方法,这种方法的基本思想是: 先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后把计数时重复计算的数目排斥出去,使得计算结果既无遗漏,又无重复,这种计数方法称为容斥原理。
容斥原理一般用在计算集合的元素个数中。

两个集合的容斥原理
设有两个非空集合 A,B，记|S!为集合S中元素的个数，则有如下关系：