【精讲】高等数学中利用等价无穷小替换求极限
博主：命运之光的主页
专栏：高等数学
目录
导言
在高等数学中，求极限是研究函数和数列趋向某个值的重要问题。有时候，我们遇到复杂的极限计算，无法直接应用传统的极限运算法则。为了简化计算过程，我们可以利用等价无穷小替换的方法来求解极限。本文将详细解释等价无穷小替换的概念、性质，以及在极限计算中的正确应用。
一、等价无穷小的概念
等价无穷小是指在极限计算中，当自变量趋于某一点时，两个无穷小量之间的差异趋向于零。换句话说，如果函数f(x)和g(x)在x=a处都为无穷小，且lim(x→a) [f(x) - g(x)] = 0，则我们称f(x)和g(x)是等价无穷小。在这种情况下，我们可以用一个无穷小量替代另一个无穷小量，以简化极限计算。
二、等价无穷小的性质
-
等价无穷小具有传递性：如果lim(x→a) [f(x) - g(x)] = 0且lim(x→a) [g(x) - h(x)] = 0，则lim(x→a) [f(x) - h(x)] = 0。换句话说，如果f(x)是g(x)的等价无穷小，而g(x)是h(x)的等价无穷小，那么f(x)也是h(x)的等价无穷小。
-
常数倍法则：如果lim(x→a) f(x) = 0，则对于任意常数c，lim(x→a) [cf(x)] = 0。这意味着常数倍的无穷小量也是等价无穷小。
三、利用等价无穷小替换求极限
利用等价无穷小替换的方法可以简化复杂极限的计算过程。以下是使用等价无穷小替换求极限的一般步骤：
- 首先，根据题目给出的极限表达式，找出可以使用等价无穷小替换的部分。
- 确定等价无穷小的形式，并计算等价无穷小的极限值。
- 将原极限中的复杂部分替换为等价无穷小，并计算新的极限值。
- 最后，得出极限的结果。
四、举例说明
假设我们要计算极限lim(x→0) sin(x)/x。在x趋向0时，分母x趋于0，而sin(x)在x=0处的极限为0。因此，我们可以将sin(x)替换为它的等价无穷小x，得到新的极限lim(x→0) x/x = lim(x→0) 1 = 1。
五、注意事项： 在使用等价无穷小替换时，需要注意以下几点：
- 等价无穷小的替换要符合极限的定义，即差异趋向于0。
- 替换后的极限结果必须与原极限等价，即两者应该是相等的。
必需记忆知识点
例题（用于熟悉高等数学中利用等价无穷小替换求极限）
例题1
例题2
例题3
例题4
例题5
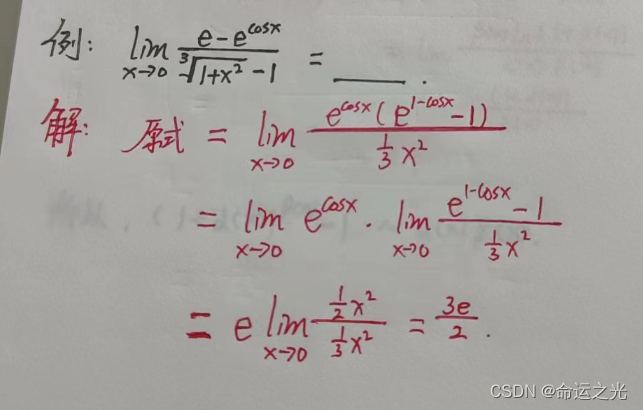
例题6
例题7
例题8
例题9
结论
等价无穷小替换是高等数学中简化极限计算的有效方法。通过将复杂的无穷小量替换为等价无穷小，我们可以简化极限计算过程，并得出准确的极限结果。在应用等价无穷小替换时，需要遵循替换的准则，并保证替换后的极限结果与原极限等价。这个方法在高等数学和相关领域的数学问题中有广泛的应用。
本章的内容就到这里了，觉得对你有帮助的话就支持一下博主把~
🌌点击下方个人名片，交流会更方便哦~
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
扫一扫
2705
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
