上一篇 隐含波动率
文章目录
编程金融小白学 股票期权
希腊字母 I
-
运用希腊字母 是对期权 比较静态的敏感分析
-
含义:其他条件不变,(某因素)变化一单位,期权价格大概变化多少?
- 标的资产价格: Delta ( Δ ) (\Delta) (Δ)
- 时间: Theta ( θ ) (\theta) (θ)
- 隐含波动率: Vega ( ϑ ) (\vartheta) (ϑ)
- 利率: Rho ( r ) (r) (r)
-
Gamma ( γ ) (\gamma) (γ): 标的价格变动1单位时,Delta Δ \Delta Δ 变多少?
波动率 Sigma ( σ ) (\sigma) (σ)
- 详情 请看上一篇 隐含波动率
Delta ( Δ ) (\Delta) (Δ) — 标的资产价格
-
标的资产价格变化一单位,期权价格大概变化多少?
-
例:
- Delta = 0.3141 意味着
- 如果指数上涨 10 点,期权价格大概上涨 3.141点
-
Δ = ∂ c ∂ S \Delta = \frac{\partial c}{\partial S} Δ=∂S∂c
-
期权价格曲线切线斜率(动态时变)
-
(无红利欧式期权)的4个特征:
特征 I
| 标的价格 | 看涨多头 | 看涨空头 | 看跌多头 | 看跌空头 |
|---|---|---|---|---|
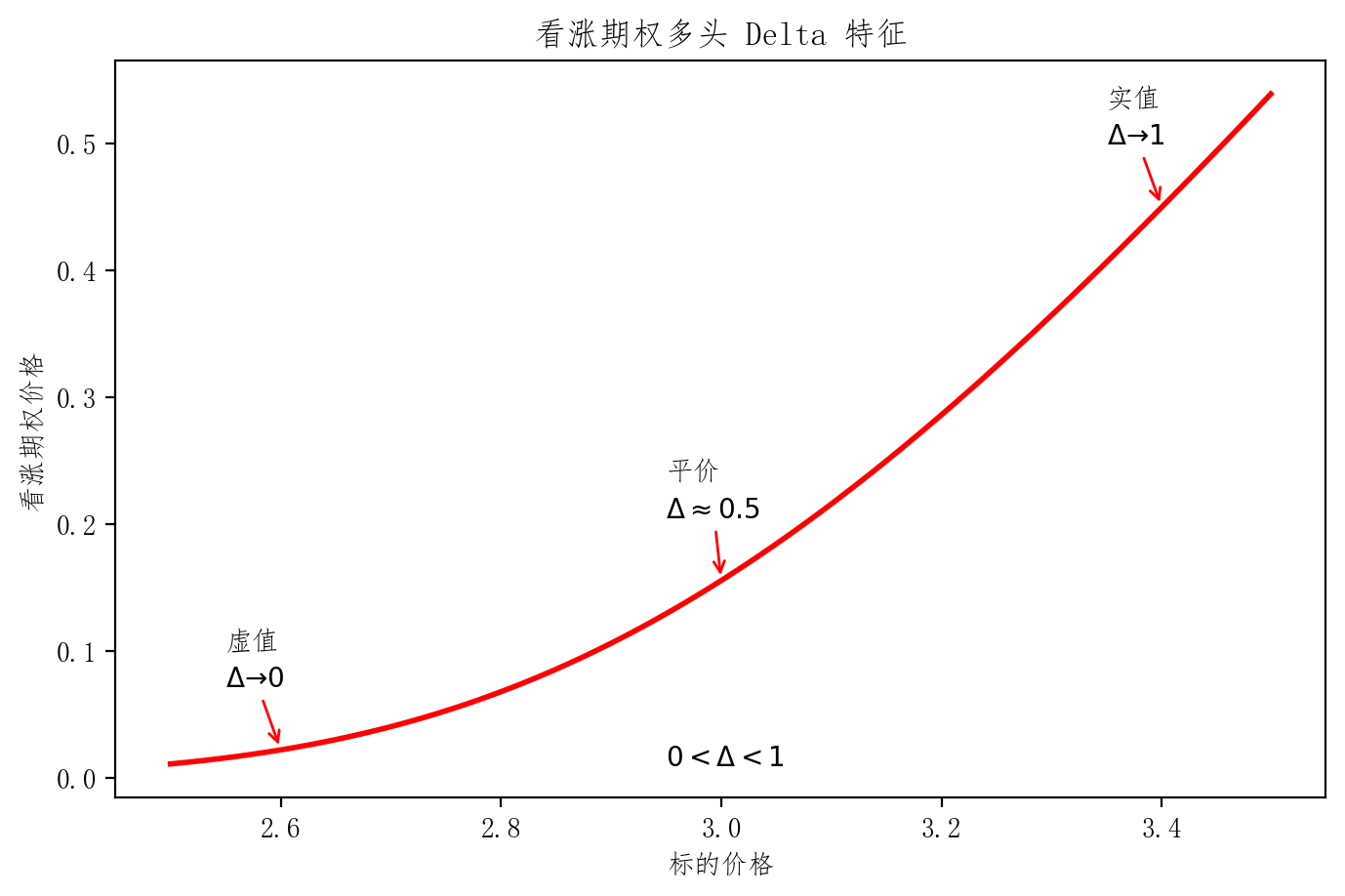
| 区间 | 0 < Δ < 1 0<\Delta<1 0<Δ<1 | 符号相反 | − 1 < Δ < 0 -1<\Delta<0 −1<Δ<0 | 符号相反 |
| 虚值 | Δ → 0 \Delta\to0 Δ→0 | Δ → 0 \Delta\to0 Δ→0 | Δ → 0 \Delta\to0 Δ→0 | Δ → 0 \Delta\to0 Δ→0 |
| 平价 | Δ ≈ 0.5 \Delta\approx0.5 Δ≈0.5 | Δ ≈ − 0.5 \Delta\approx-0.5 Δ≈−0.5 | Δ ≈ − 0.5 \Delta\approx-0.5 Δ≈−0.5 | Δ ≈ 0.5 \Delta\approx0.5 Δ≈0.5 |
| 实值 | Δ → 1 \Delta\to1 Δ→1 | Δ → − 1 \Delta\to-1 Δ→−1 | Δ → − 1 \Delta\to-1 Δ→−1 | Δ → 1 \Delta\to1 Δ→1 |
- 利用上篇的BS定价模型绘制图像 更好的去理解
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt # 画图
plt.rcParams['font.sans-serif'] = ['FangSong'] # 设置中文
plt.rcParams['axes.unicode_minus'] = False # 设置中文负号
class BlackScholes:
def __init__(self, S0, X, r, T, sigma=0.3,t=0):
self.S0 = S0
self.X = X
self.r = r
self.sigma = sigma
self.dT = T-t
def d1(self):
return(np.log(self.S0/self.X)+(self.r+self.sigma**2/2)*(self.dT))/(self.sigma*np.sqrt(self.dT))
def d2(self):
return self.d1()-self.sigma*np.sqrt(self.dT)
def calc(self, call_put):
if call_put in {'c','C','call','Call','CALL'}:
return self.S0 * norm.cdf(self.d1())- \
self.X*np.exp(-self.r*self.dT)*norm.cdf(self.d2())
elif call_put in {'p','P','put','Put','PUT'}:
return self.X*np.exp(-self.r*self.dT)*norm.cdf(-self.d2())- \
self.S0 * norm.cdf(-self.d1())
raise NameError('Must be call or Put!',call_put)
def imp_vol(self,call_put,mktprice):
price = 0
sigma = 0.3
up, low = 1,0
loop = 0
while abs(price-mktprice)>1e-6 and loop<50:
price = BlackScholes(self.S0,self.X,self.r,self.dT,sigma).calc(call_put)
if (price-mktprice)>0:
up = sigma
sigma = (sigma+low)/2
else:
low = sigma
sigma = (sigma+up)/2
loop+=1
return sigma
# 标的价格S做自变量 求因变量c
S = np.arange(2.5,3.5,0.001)
BS = [BlackScholes(s,3., 0.05, 0.16)for s in S]
c = np.array([bs.calc('c') for bs in BS])
# 绘图
plt.figure(figsize=(8,5), dpi=200)
plt.plot(S,c,'r',lw=2)
annotate_x=[2.6,3.,3.4]
annotate_y=[BlackScholes(s,3., 0.05, 0.16).calc('c') for s in annotate_x]
annotate_name = ['虚值','平价','实值']
annotate_symbol= [r'$\Delta \to 0$',r'$\Delta \approx 0.5$',r'$\Delta \to 1$']
for x,y,z,s in zip(annotate_x,annotate_y,annotate_name,annotate_symbol):
plt.annotate(z,xy=(x-0.05,y+0.08),weight="bold")
plt.annotate(s,xy=(x,y),xytext=(x-0.05,y+0.05),arrowprops=dict(arrowstyle='->',connectionstyle="arc3",color="r"))
plt.annotate(r'$0<\Delta<1$',xy=(2.95,0.01))
plt.xlabel('标的价格')
plt.ylabel('看涨期权价格')
plt.title('看涨期权多头 Delta 特征')
plt.show()
# 标的价格S做自变量 求因变量c
c = np.array([-1*bs.calc('c') for bs in BS])
plt.figure(figsize=(8,5), dpi=200)
plt.plot(S,c,'r',lw=2)
annotate_x=[2.6,3.,3.4]
annotate_y=[-1*BlackScholes(s,3., 0.05, 0.16).calc('c') for s in annotate_x]
annotate_name = ['虚值','平价','实值']
annotate_symbol= [r'$\Delta \to 0$',r'$\Delta \approx -0.5$',r'$\Delta \to -1$']
for x,y,z,s in zip(annotate_x,annotate_y,annotate_name,annotate_symbol):
plt.annotate(z,xy=(x-0.1,y-0.08),weight="bold")
plt.annotate(s,xy=(x,y),xytext=(x-0.1,y-0.05),arrowprops=dict(arrowstyle='->',connectionstyle="arc3",color="r"))
plt.annotate(r'$0>\Delta>-1$',xy=(2.95,-0.5))
plt.xlabel('标的价格')
plt.ylabel('看涨期权价格')
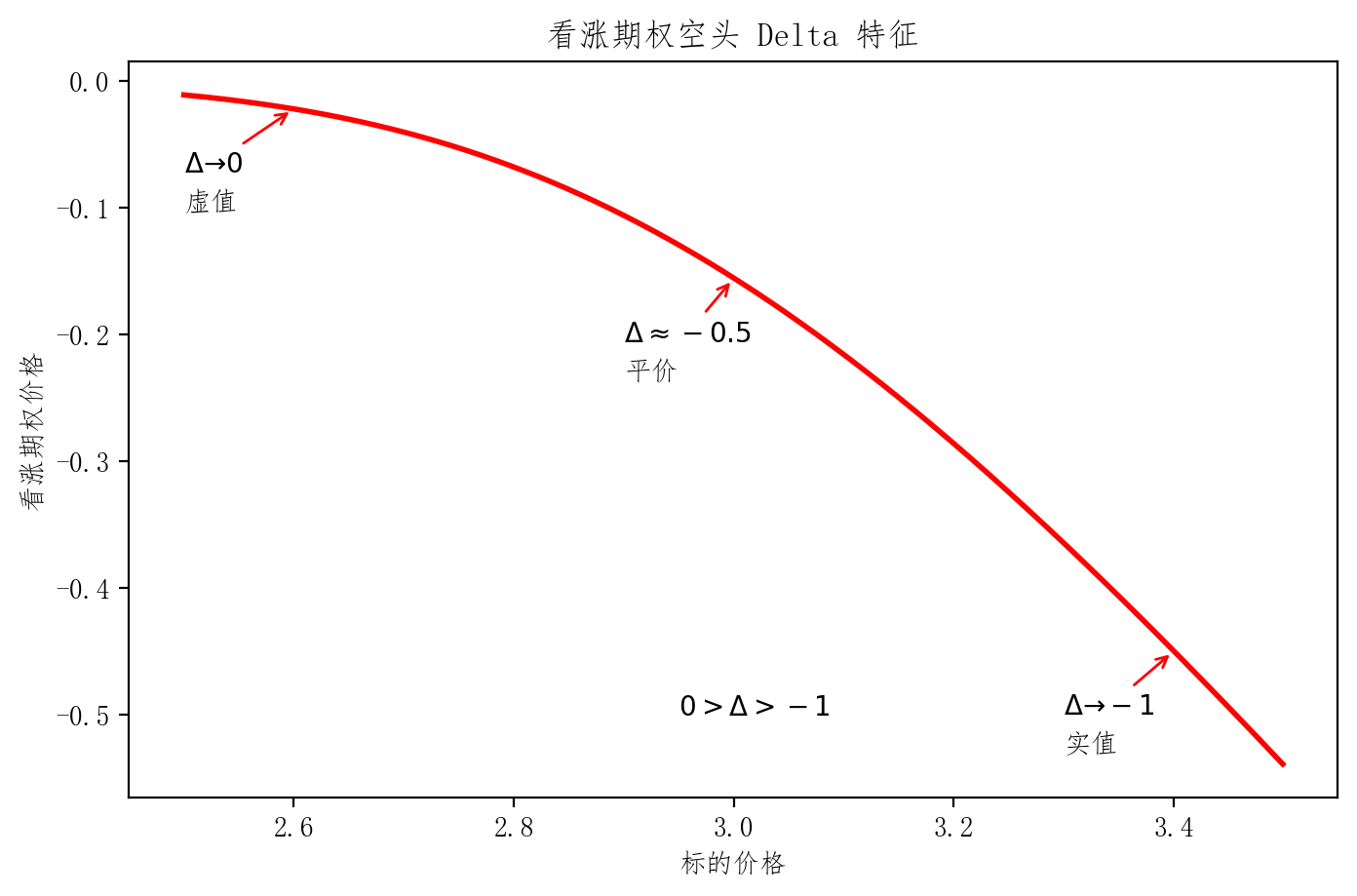
plt.title('看涨期权空头 Delta 特征')
plt.show()
# 标的价格S做自变量 求因变量p
p = np.array([bs.calc('p') for bs in BS])
plt.figure(figsize=(8,5), dpi=200)
plt.plot(S,p,'r',lw=2)
annotate_x=[2.6,3.,3.4]
annotate_y=[BlackScholes(s,3., 0.05, 0.16).calc('p') for s in annotate_x]
annotate_name = ['实值','平价','虚值']
annotate_symbol= [r'$\Delta \to -1$',r'$\Delta \approx -0.5$',r'$\Delta \to 0$']
for x,y,z,s in zip(annotate_x,annotate_y,annotate_name,annotate_symbol):
plt.annotate(z,xy=(x-0.05,y+0.08),weight="bold")
plt.annotate(s,xy=(x,y),xytext=(x-0.05,y+0.05),arrowprops=dict(arrowstyle='->',connectionstyle="arc3",color="r"))
plt.annotate(r'$-1<\Delta<0$',xy=(2.9,0.01))
plt.xlabel('标的价格')
plt.ylabel('看跌期权价格')
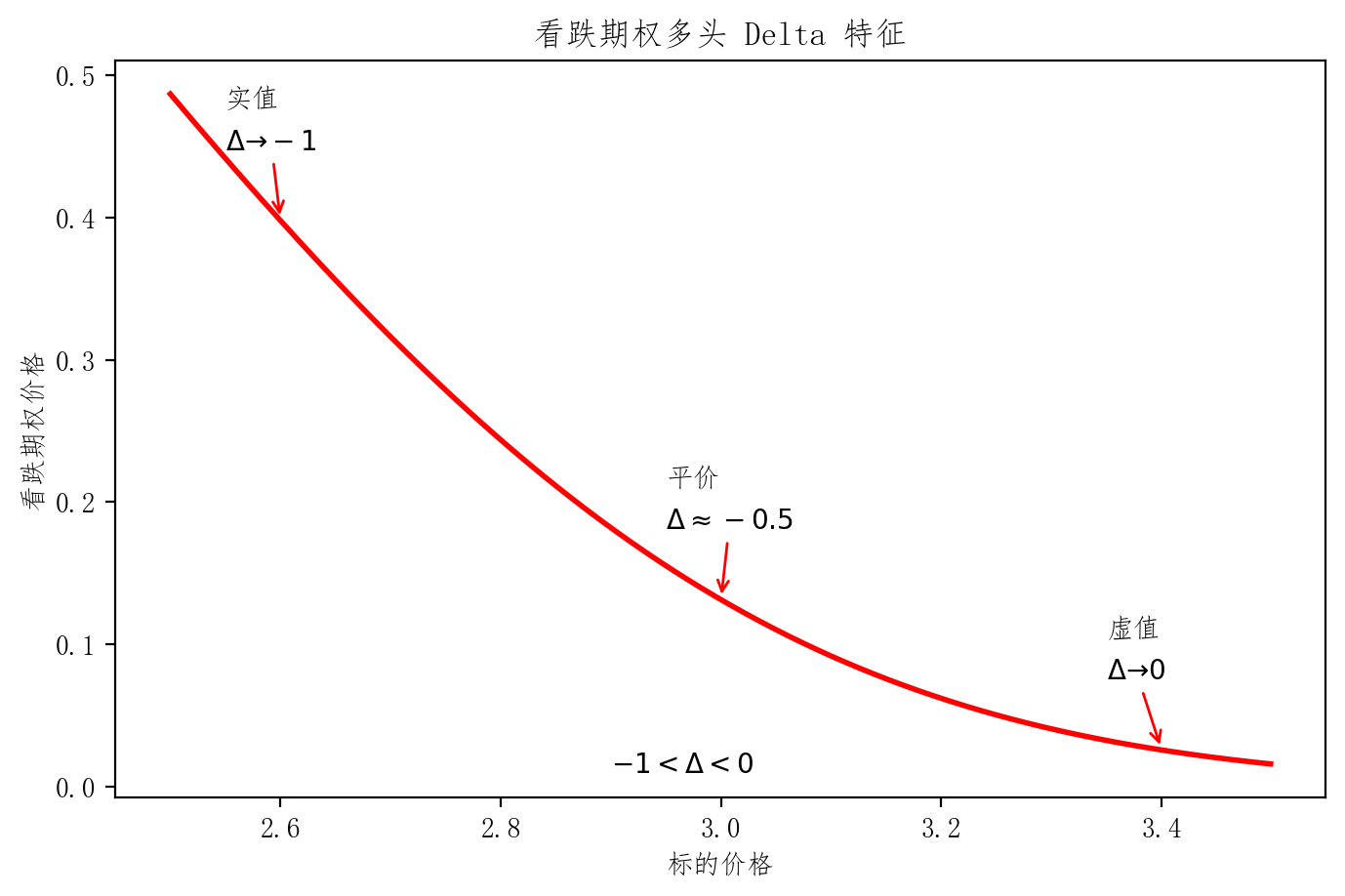
plt.title('看跌期权多头 Delta 特征')
plt.show()
# 标的价格S做自变量 求因变量p
p = np.array([-1*bs.calc('p') for bs in BS])
plt.figure(figsize=(8,5), dpi=200)
plt.plot(S,p,'r',lw=2)
annotate_x=[2.6,3.,3.4]
annotate_y=[-1*BlackScholes(s,3., 0.05, 0.16).calc('p') for s in annotate_x]
annotate_name = ['实值','平价','虚值']
annotate_symbol= [r'$\Delta \to 1$',r'$\Delta \approx 0.5$',r'$\Delta \to 0$']
for x,y,z,s in zip(annotate_x,annotate_y,annotate_name,annotate_symbol):
plt.annotate(z,xy=(x-0.05,y-0.08),weight="bold")
plt.annotate(s,xy=(x,y),xytext=(x-0.05,y-0.05),arrowprops=dict(arrowstyle='->',connectionstyle="arc3",color="r"))
plt.annotate(r'$1>\Delta>0$',xy=(2.95,-0.5))
plt.xlabel('标的价格')
plt.ylabel('看跌期权价格')
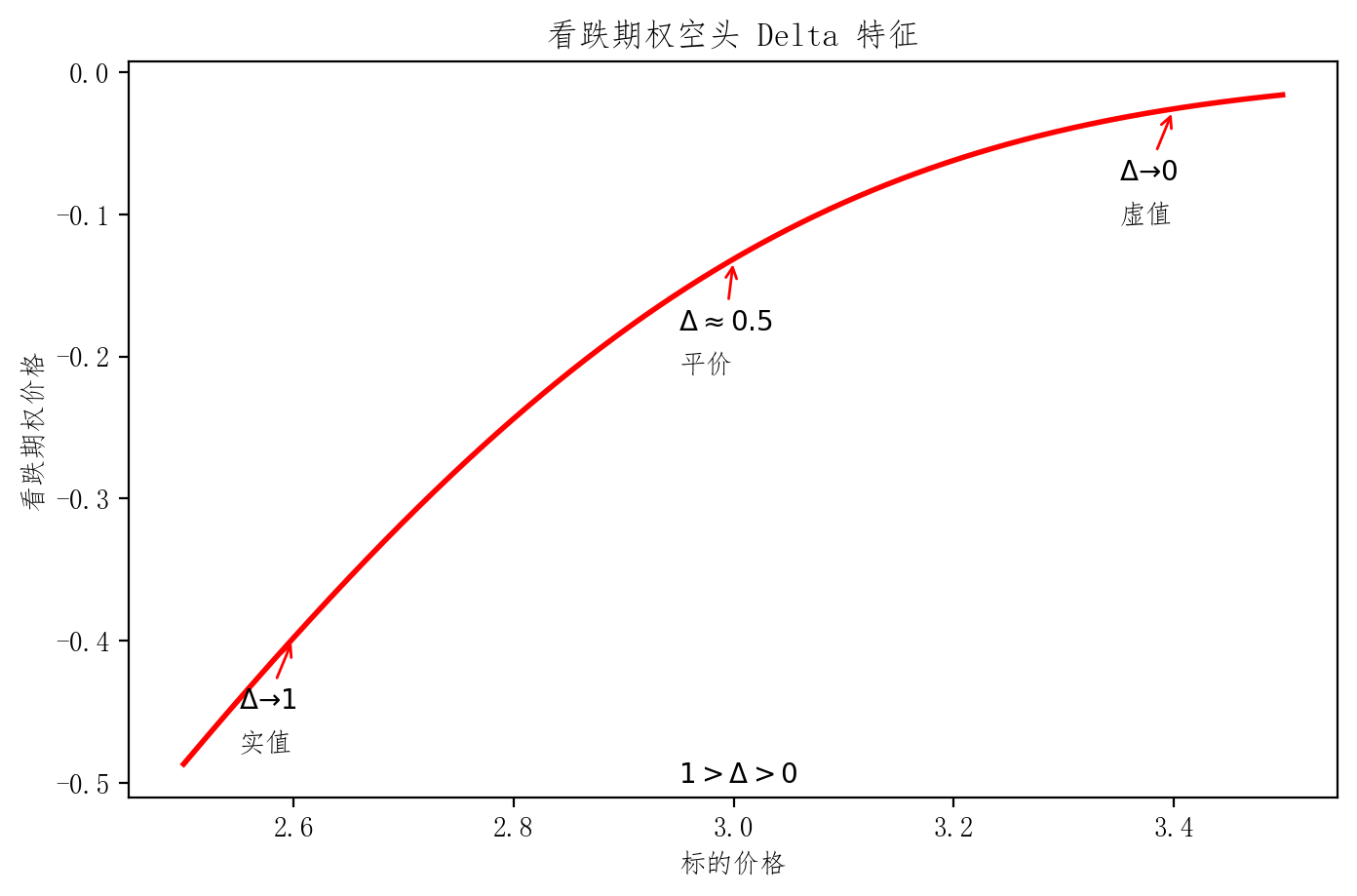
plt.title('看跌期权空头 Delta 特征')
plt.show()
特征 II
- PCP 平价原理
- 看 涨 期 权 D e l t a = 看 跌 期 权 D e l t a + 1 看涨期权 Delta = 看跌期权 Delta + 1 看涨期权Delta=看跌期权Delta+1
c + X 1 + r ( T − t ) = p + S → ∂ c ∂ S = ∂ p ∂ S + 1 c + \frac{X}{1+r(T-t)}=p+S \to \frac{\partial c}{\partial S}= \frac{\partial p}{\partial S}+1 c+1+r(T−t)X=p+S→∂S∂c=∂S∂p+1
# 其实没必要这么复杂。。。
from sklearn import linear_model
def d1(X,Y,Window=5):
result_x, result_y = [],[]
step = Window//2
for i in range(len(X)-Window):
reg = linear_model.LinearRegression()
reg.fit(X[i:i+Window].reshape(-1,1),Y[i:i+Window].reshape(-1,1))
result_y.append(reg.coef_[0][0])
result_x.append(X[i+step])
return result_x,result_y
bc = np.array([bs.calc('c') for bs in BS]) # Buy Call
bp = np.array([bs.calc('p') for bs in BS]) # Buy Put
bc_x,bc_y = d1(S,bc) # Buy Call Delta
bp_x,bp_y = d1(S,bp) # Buy Put Delta
plt.figure(figsize=(8,5), dpi=200)
plt.plot(bc_x,bc_y,'r',label='Call')
plt.plot(bp_x,bp_y,'green',label='Put')
plt.legend(loc='best')
plt.ylabel('Delta 值')
plt.xlabel('标的价格')
plt.grid(True)
plt.show()
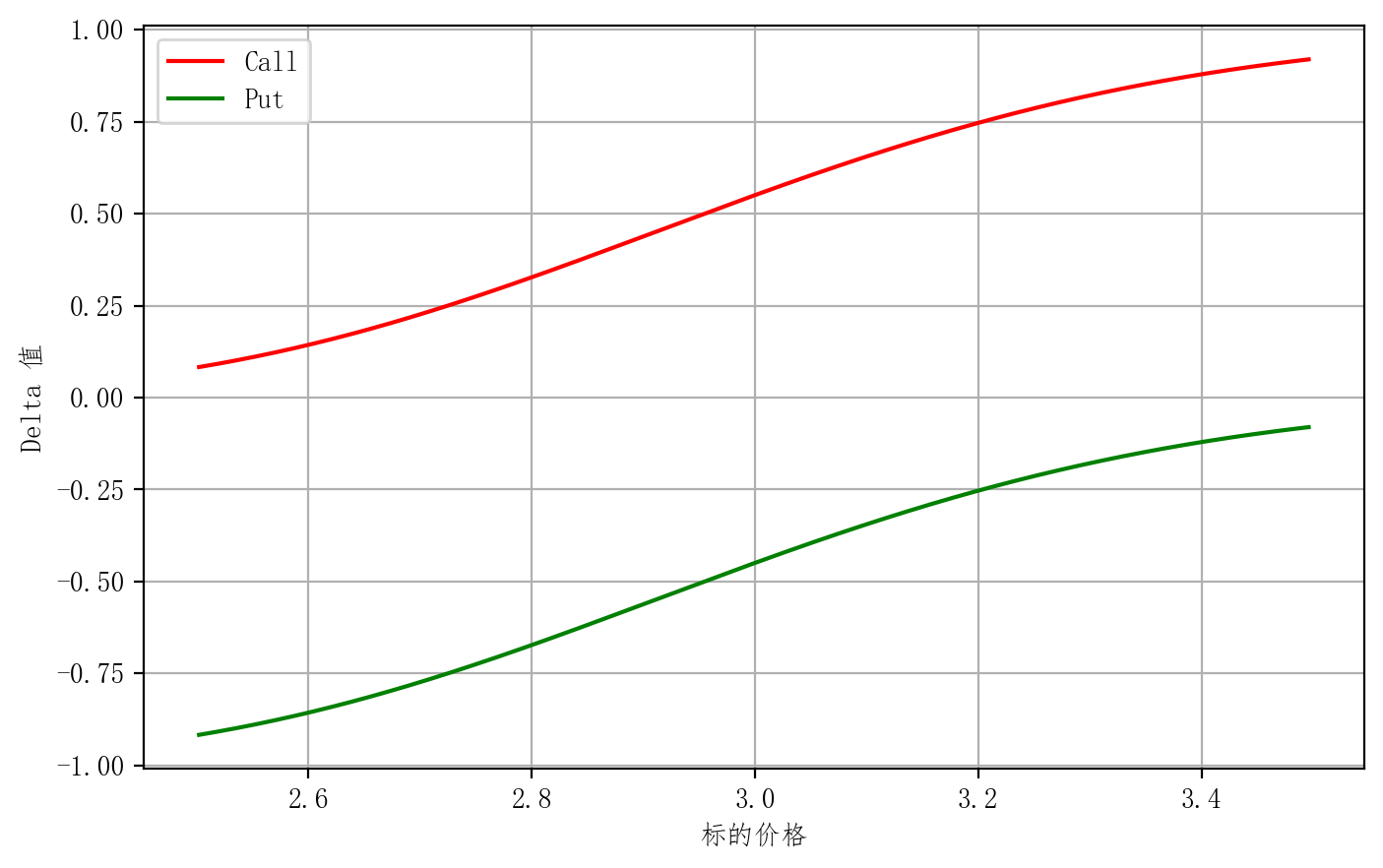
- 如图,可以看出来 他们的Delta 相差1
特征 III
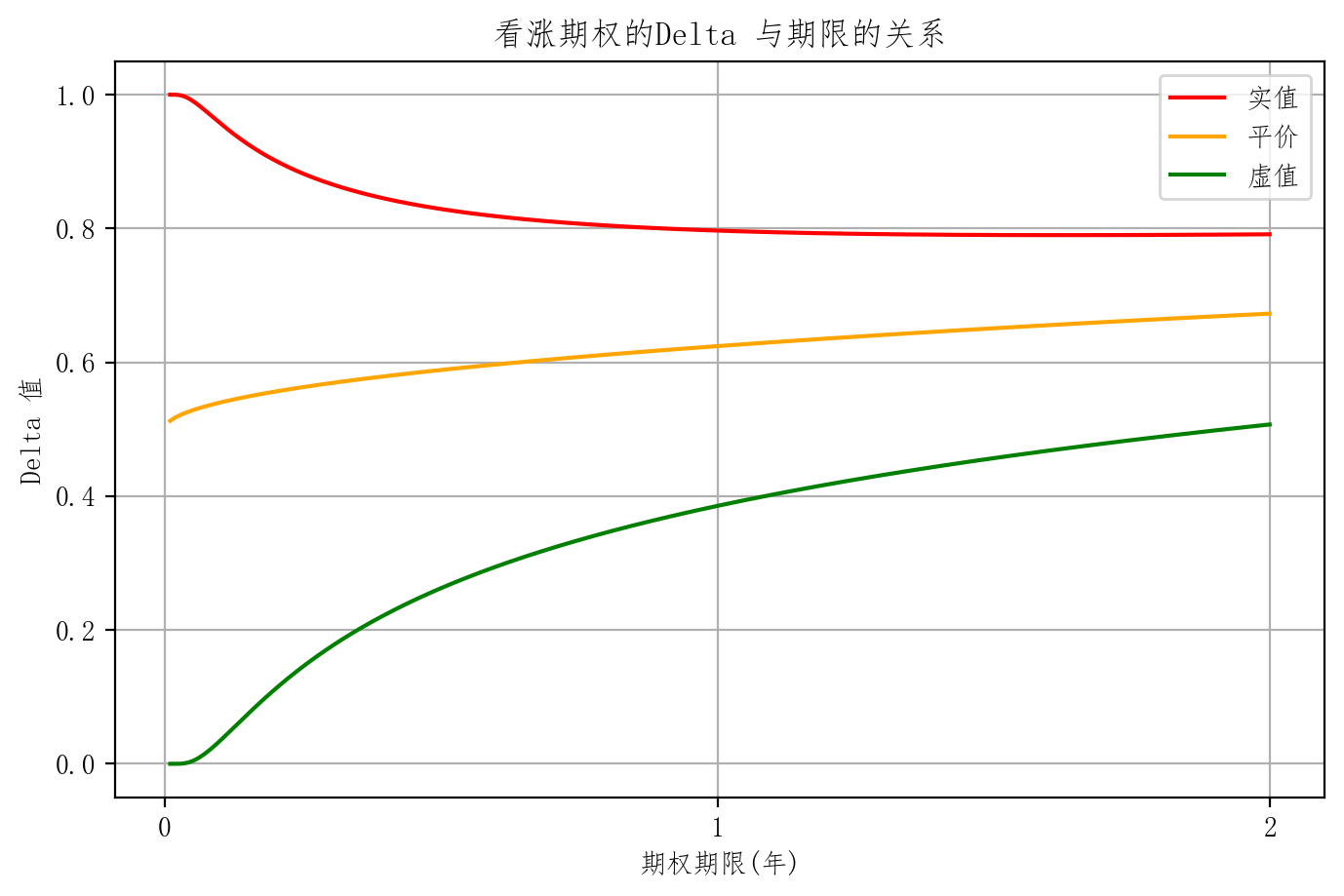
- 快到期时,实值、虚值、和平值期权的Delta 差异比较大
- 剩余期限比较大的话 时间价值比较大 它的期权价格曲线相对平滑,所以它的切线斜率比较小
T = np.arange(0.01,2,0.001)
BS_T_r = [(BlackScholes(3.49,3., 0.05, t),BlackScholes(3.51,3., 0.05, t)) for t in T] # 实值
BS_T_e = [(BlackScholes(2.99,3., 0.05, t),BlackScholes(3.01,3., 0.05, t)) for t in T] # 平价
BS_T_i = [(BlackScholes(2.49,3., 0.05, t),BlackScholes(2.51,3., 0.05, t)) for t in T] # 虚值
plt.figure(figsize=(8,5), dpi=200)
for BS_T,labels,color in zip([BS_T_r,BS_T_e,BS_T_i],['实值','平价','虚值'],['r','orange','g']):
bc = np.array([(bs2.calc('c')-bs1.calc('c'))/0.02 for bs1,bs2 in BS_T]) # Buy Call Delta
plt.plot(T,bc,color,label=labels)
plt.legend(loc='best')
plt.ylabel('Delta 值')
plt.title('看涨期权的Delta 与期限的关系')
plt.xlabel('期权期限(年)')
plt.xticks([0,1,2])
plt.grid(True)
plt.show()
plt.figure(figsize=(8,5), dpi=200)
for BS_T,labels,color in zip([BS_T_r,BS_T_e,BS_T_i],['虚值','平价','实值'],['g','orange','r']):# 与认购相反
bp = np.array([(bs2.calc('p')-bs1.calc('p'))/0.02 for bs1,bs2 in BS_T]) # Buy Call Delta
plt.plot(T,bp,color,label=labels)
plt.legend(loc='best')
plt.ylabel('Delta 值')
plt.title('看跌期权的Delta 与期限的关系')
plt.xlabel('期权期限(年)')
plt.xticks([0,1,2])
plt.grid(True)
plt.show()
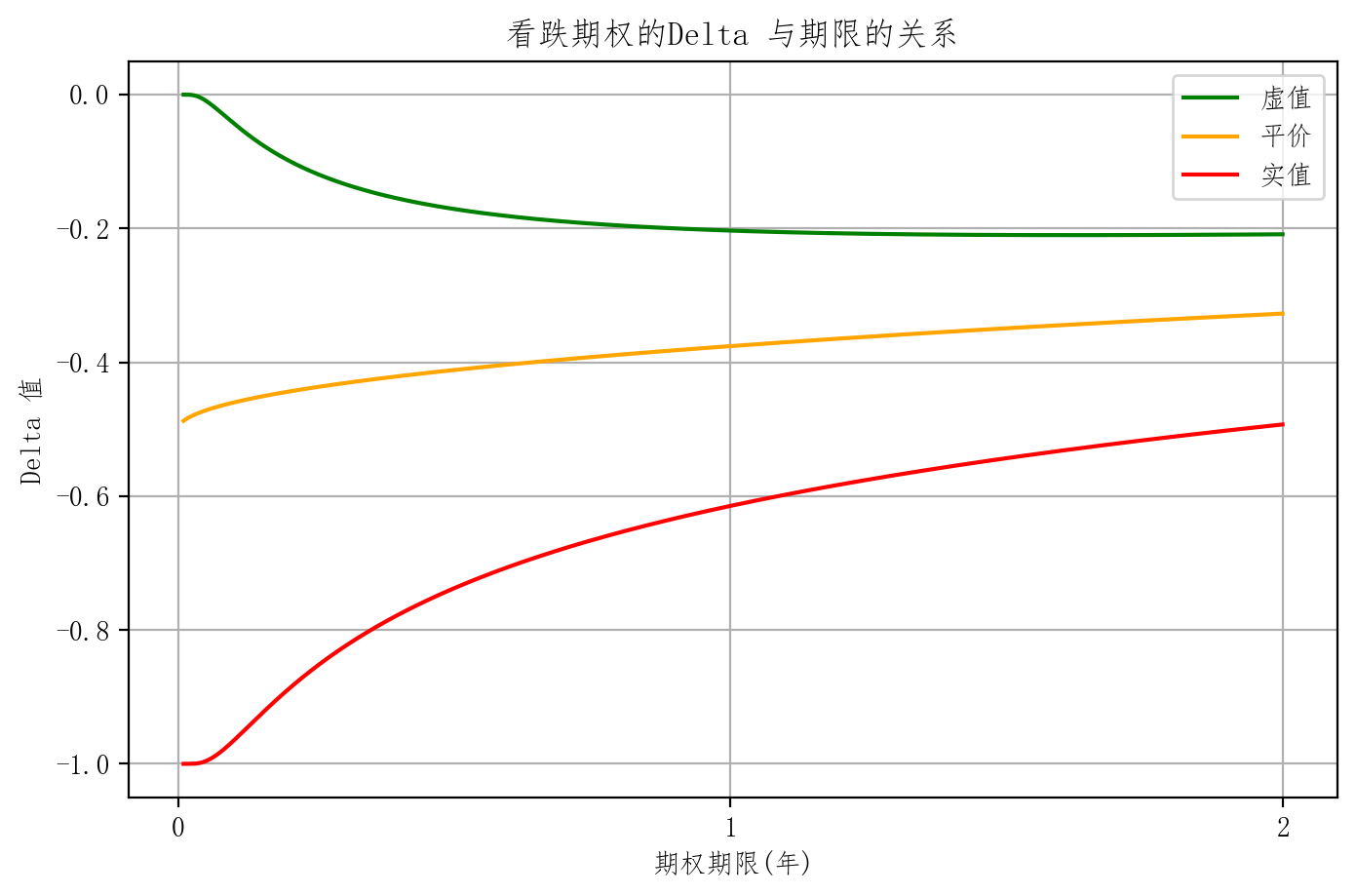
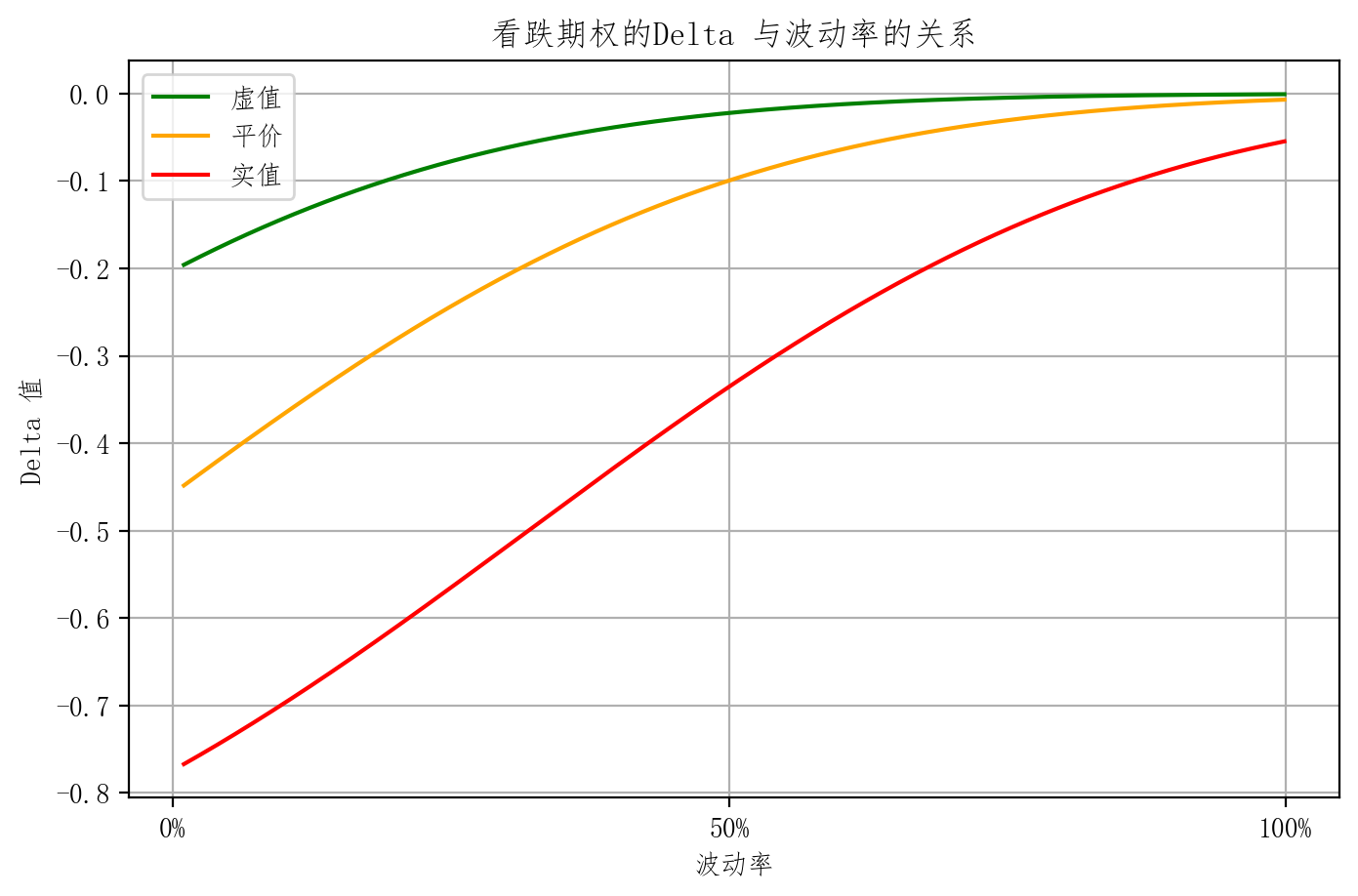
特征 IV
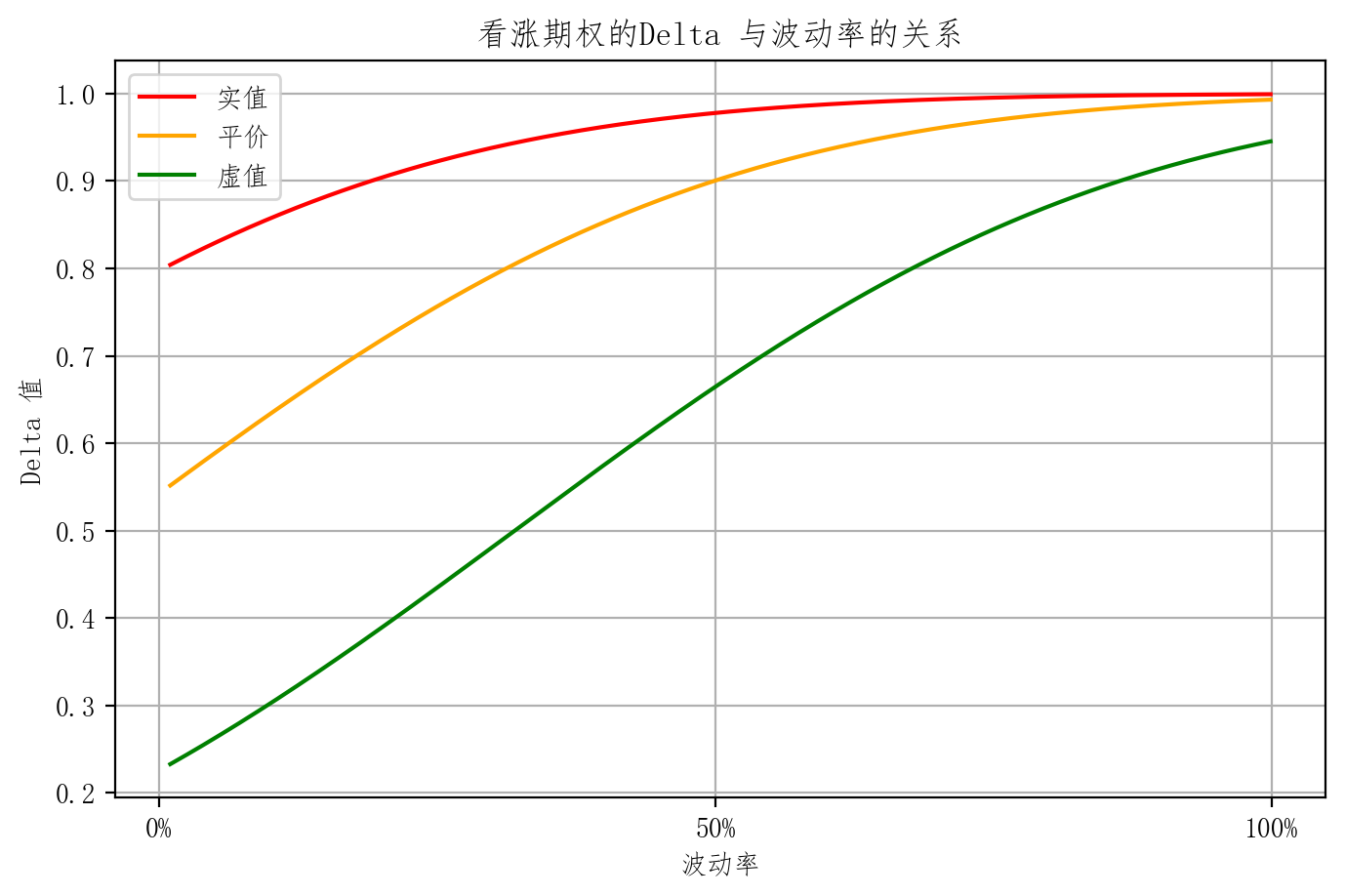
- 波动率较低时,实值、虚值、和平值期权的Delta 差异比较大
- 原理与特征 III 相同
Sigma = np.arange(0.01,1,0.001)
t = 0.5
BS_S_r = [(BlackScholes(3.49,3., sigma, t),BlackScholes(3.51,3., sigma, t)) for sigma in Sigma] # 实值
BS_S_e = [(BlackScholes(2.99,3., sigma, t),BlackScholes(3.01,3., sigma, t)) for sigma in Sigma] # 平价
BS_S_i = [(BlackScholes(2.49,3., sigma, t),BlackScholes(2.51,3., sigma, t)) for sigma in Sigma] # 虚值
plt.figure(figsize=(8,5), dpi=200)
for BS_S,labels,color in zip([BS_S_r,BS_S_e,BS_S_i],['实值','平价','虚值'],['r','orange','g']):
bc = np.array([(bs2.calc('c')-bs1.calc('c'))/0.02 for bs1,bs2 in BS_S]) # Buy Call Delta
plt.plot(Sigma,bc,color,label=labels)
plt.legend(loc='best')
plt.ylabel('Delta 值')
plt.title('看涨期权的Delta 与波动率的关系')
plt.xlabel('波动率')
plt.xticks([0,0.5,1],['0%','50%','100%'])
plt.grid(True)
plt.show()
plt.figure(figsize=(8,5), dpi=200)
for BS_S,labels,color in zip([BS_S_r,BS_S_e,BS_S_i],['虚值','平价','实值'],['g','orange','r']):# 与认购相反
bp = np.array([(bs2.calc('p')-bs1.calc('p'))/0.02 for bs1,bs2 in BS_S]) # Buy Call Delta
plt.plot(Sigma,bp,color,label=labels)
plt.legend(loc='best')
plt.ylabel('Delta 值')
plt.title('看跌期权的Delta 与波动率的关系')
plt.xlabel('波动率')
plt.xticks([0,0.5,1],['0%','50%','100%'])
plt.grid(True)
plt.show()
证券组合的 Delta 值
| 头寸 | Delta | 例子(N为数量) |
|---|---|---|
| 现货多头 | 1 | 4单位: 4 × 1 = 4 4\times 1 =4 4×1=4 |
| 现货空头 | -1 | 3单位: 3 × − 1 = − 3 3\times -1 =-3 3×−1=−3 |
| 期货多头 | 1 | 2单位: 2 × 1 = 2 2\times 1 =2 2×1=2 |
| 现货多头 | -1 | 5单位: 5 × − 1 = − 5 5\times -1 =-5 5×−1=−5 |
| 欧式看涨期权多头 (无红利) | 0 < Δ < 1 0<\Delta<1 0<Δ<1 | 5单位多头,每单位Delta为0.5: 5 × 0.5 = 2.5 5\times 0.5 =2.5 5×0.5=2.5 |
| 欧式看涨期权空头 (无红利) | − 1 < Δ < 0 -1<\Delta<0 −1<Δ<0 | 4单位多头,每单位Delta为-0.4: 4 × − 0.4 = − 1.6 4\times -0.4 =-1.6 4×−0.4=−1.6 |
| 欧式看跌期权多头 (无红利) | − 1 < Δ < 0 -1<\Delta<0 −1<Δ<0 | 3单位多头,每单位Delta为-0.5: 3 × − 0.5 = − 1.5 3\times -0.5 =-1.5 3×−0.5=−1.5 |
| 欧式看跌期权空头 (无红利) | 0 < Δ < 1 0<\Delta<1 0<Δ<1 | 2单位多头,每单位Delta为0.6: 2 × 0.6 = 1.2 2\times 0.6 =1.2 2×0.6=1.2 |
| 投资组合 | ∑ i N i ⋅ Δ i ↑ \sum_i N_i\cdot\Delta_i\uparrow i∑Ni⋅Δi↑ |
Delta 中性
- 在投资组合中 让Delta 为0 称 Delta 中性
- 意味着 投资组合对现货价格变动的一阶敏感性为 0
- 实现:运用同一标的资产的现货,期货和期权等进行相互套期保值,使证券组合的值等于0
- 特点:有期权的情况下是动态的,需要不懂调整头寸以使组合重新处于 Δ \Delta Δ中性状态,这种调整称为再均衡(Rebalancing)。
Theta ( θ ) (\theta) (θ) — 时间
-
时间变化一天,期权价格大概变化多少?
-
Time 时间
-
例:
- Theta = 1.234 意味着
- 时间每过一天,期权价格大概上涨 1.234点
Vega ( ϑ ) (\vartheta) (ϑ) — 隐含波动率
-
隐含波动率变化一百分点,期权价格大概变化多少?
-
Volatility 隐含波动率
-
例:
- Vega = 1.878 意味着
- 每隐含波动率上升1%,期权价格大概上涨 1.878点
Rho ( r ) (r) (r) — 利率
- Rate 利率
Gamma
- 例:
- Gamma = 0.0056,Delta = 0.3141 意味着
- 如果指数上涨 10 点,Delta大概上升至 0.3141 + 10 ∗ 0.0056 = 0.3701 0.3141+10*0.0056 = 0.3701 0.3141+10∗0.0056=0.3701
- 如果指数下跌 10 点,Delta大概下降至 0.3141 − 10 ∗ 0.0056 = 0.2581 0.3141-10*0.0056 = 0.2581 0.3141−10∗0.0056=0.2581





















 491
491











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








