第一章补充：多元微分学合集（B站小崔说数）_某点左右导数相同说明什么-CSDN博客

本文链接：https://blog.csdn.net/Vincent_Zhang233/article/details/142927559

容易混淆的知识点汇总：

函数 $f(x)$ 在点 $(x_{0},y_{0})$ 处极限存在和函数 $f(x)$ 在点 $(x_{0},y_{0})$ 处可导的区别：

1）函数 $f(x)$ 在点 $(x_{0},y_{0})$ 处极限存在：

意味着 $\lim_{x\rightarrow x^{-}_{0}}f(x)=\lim_{x\rightarrow x^{+}_{0}}f(x)=A$ ，其中 $A$ 不一定等于 $f(x_{0})$ 。如果 $A=f(x_{0})$ ，则函数在该点处连续；如果 $A\neq f(x_{0})$ ，则函数在该点处不连续。

2）函数 $f(x)$ 在点 $(x_{0},y_{0})$ 处可导：

如果函数在某点处的左导数和右导数相等，则说明函数在该点处可导。

函数在点 $(x_{0},y_{0})$ 处可导，意味着 $\lim_{x\rightarrow x_{0}}\frac{f(x)-f(x_{0})}{x-x_{0}}=A$ ，

由于 $x\rightarrow x_{0}$ ，则 $(x-x_{0})\rightarrow 0$ ，所以 $f(x)-f(x_{0})$ 必须也得趋近于0，这个极限才能存在。

所以，可以推导出： $\lim_{x\rightarrow 0}[f(x)-f(x_{0})]=0$ ，即：当 $x\rightarrow x_{0}$ 时， $f(x)=f(x_{0})$ ，即：极限值=函数值，而这就是函数在该点处连续的定义。所以，可导必连续。

视频1：多元函数的连续性

原视频：【多元微分专题1】多元函数的连续性到底在讲什么？_哔哩哔哩_bilibili

上图中，D是自变量x和y的定义域，上面的曲面就是多元函数的图像。

上面是两个比较特殊的曲面，左边是一个半球面，右边是一个空间里的旋转抛物面。

一、一元函数的极限与连续

一元函数的极限与连续是怎么定义的？

1、一元函数的极限

极限：一元函数在 $x_{0}$ 点处的极限存在，则 $\lim_{x\rightarrow x_{0}}f(x)=A$

它的几何意义就是：当 $x$ 跑向 $x_{0}$ 的时候，自变量在跑，那么因变量肯定也在跑，因变量跑向A。学过高数上册的同学都明白，函数的极限是定义在去心邻域上的，或者说是定义在一个特别特别小的区域，写作：，而定义在去心邻域上，要往 $x_{0}$ 跑，自变量毫无疑问是定义在一根线段上的，它要往 $x_{0}$ 方向越跑越近，只能是左右两边都朝着 $x_{0}$ 的方向跑。

所以，一元函数极限存在的一个充要条件就是：自变量从左边和右边跑向同一个点 $x_{0}$ 的时候，因变量也跑向同一个数A，公式如下：

2、一元函数的连续

那么，一元函数的连续是怎么定义的呢？

首先，要确定一元函数在这个点 $x_{0}$ 上是否有定义，即： $f(x_{0})=A$

第二，要确定一元函数在这个点上是否有极限，即：

$\lim_{x\rightarrow x_{0}^{+}}f(x)=\lim_{x\rightarrow x_{0}^{-}}f(x)=B=\lim_{x\rightarrow x_{0}}f(x)$

第三，一元函数连续的充要条件就是：函数在该点处的极限值等于函数在该点处的实际值。如下公式所示：

上图的意思就是： $\lim_{x\rightarrow x_{0}^{+}}f(x)=\lim_{x\rightarrow x_{0}^{-}}f(x)=B=\lim_{x\rightarrow x_{0}}f(x)=f(x_{0})=A$

即： $\lim_{x\rightarrow x_{0}}f(x)=f(x_{0})$

所以，你去判断一个函数在某点处是否连续，关键还是看那个极限，因为实际函数在该点处是否有定义，实际值是多少这个我们一般都是知道的，而求极限相对复杂一些。

注意：当函数不连续的时候，也是有可能存在极限的。如下图👇

3、一元函数的极限与连续总结

连续则极限必存在

极限存在不一定连续（除非函数在该点的极限值等于函数在该点的实际值，那么函数在该点处连续）

二、多元函数的极限与连续

那么，以上两张图是否能说明极限存在？即当 $(x,y)\rightarrow (0,0)$ 时， $z\rightarrow 0$ 吗？实际上是不行的。因为这只是两种趋近方式而已，我们说的是所有趋近方式下z的值都要相等。所以，理论上仅有这两种趋近方式是不行的。但是仅针对 $z=x^{2}+y^{2}$ 这个函数，其实你一写出来就知道这个函数是肉眼可见的连续。

当然，这里又有一个连续的概念：一元函数的连续是一元函数的极限值等于它的函数值；多元函数的连续就是多元函数的极限值等于它的函数值。而上面的函数 $z=x^{2}+y^{2}$ 显然是相等的。

到这里，可能有的同学会疑惑：极限存在或连续的函数很好想象，那极限不存在或不连续的呢？其实这个也有，您往下看！

比如上面这个例子，我们选取沿着x轴，从左右两边跑向（0,0）这个点，如下图所示：

显然，上图函数的左右极限没有跑向同一个值，所以在（0,0）点处函数的极限是不存在的。既然在（0,0）点处极限都不存在，那么在（0,0）点处自然也就不可能连续了。

以上就是函数的极限不存在，或者不连续的一个例子。

四、总结：一元函数、多元函数极限与连续的关系总结

1、无论是一元函数还是多元函数，只要连续，则极限必存在

2、无论是一元函数还是多元函数，极限存在不一定连续

除非多元函数的自变量在所有趋近方式下得到的极限值都等于函数在该点的实际值，这时才可以确定多元函数在该点处连续。但是这个证明比较困难，考试一般也不会这么考，通常是考察函数不连续的情况。

三、例题

做这样的题目时，可以先记一个小原则：绝大多数题目考你的都是不存在的。因为验证函数的极限存在这太复杂了，它需要把每一种趋近方式都验证完整，这从数学上来讲显然是不可能的。所以，往往都是让我们去证明不存在。“不存在”的证明就很简单了，你只需要找到任意的两种趋近方式下它的极限值不相同就可以了。所以证明“不存在”是多一点的。当然，也有一些证明“存在”的题目。

上面例题中，显然极限是不存在的，因为只要k不相同，极限值就不相同。即：只要x和y趋近（0,0）点的方式不同，那么函数的极限值就不一样，而如果极限存在，那么任何一种x和y向（0，0）点的逼近，极限都应该是相同的。

视频2：直观理解偏导数的定义

原视频：【多元微分专题2】直观理解偏导数的定义_哔哩哔哩_bilibili

一、类比一元函数的偏导数

老规矩，我们先用一元函数做一下类比。在一元函数中，偏导数叫做“导数”。

导数是如何定义的？

首先，导数的几何意义是“切线斜率”。说白了就是y关于x的变化率。表达式如下：

二、偏导数

我们知道，偏导数的研究对象是多元函数。而多元函数是有2个自变量的，说白了就是在 $(x_{0},y_{0})$ 点处， $x$ 和 $y$ 都是可以变化的。

前面一元函数中我们是研究因变量关于自变量的变化率，现在我们也想研究因变量关于自变量的变化率，即z关于x的变化率，也就是x动，y不动。

上图中，是关于x的偏导数图像，说白了就是让y恒定，让x随意变化。然后求函数在（x0，y0）点的斜率。

同理，关于y的偏导数就是让x恒定，y随意变化，然后求函数在（x0，y0）点的斜率。

在学习偏导数的时候，要注意两个方面：

1、要知道它的定义是什么。

2、要知道它的几何意义是什么。

视频3：多元函数连续和可偏导之间的关系

原视频：【多元微分专题3】多元连续和可偏导之间的关系_哔哩哔哩_bilibili

在高数上册我们学过“可导必连续，连续未必可导”的概念；在高数下册我们学过“可偏导”和“连续”这两个概念。那么这个“可偏导”和“连续”之间有什么关系呢？是不是和上册差不多呢？本专题就对此进行讲解。

一、一元函数的可导和连续

一元函数遵循“可导必连续，连续未必可导”的概念。

那么，接下来我们就来证明一下为什么“可导必连续，连续未必可导”这个概念。

1、证明一元函数“可导必连续”概念

所谓“可导”，就意味着下面👇的极限是存在的。

当上面这个极限成立，那么毫无疑问，这个式子的分母 $x-x_{0}$ 是无穷小，那么分子 $f(x)-f(x_{0})$ 必须也是无穷小，因为必须是无穷小比无穷小，这个极限才能存在。

由此，可以推到出下面👇的式子：

即：

极限值=函数值，而这不就是连续的定义么！！！所以，可导必连续。

2、证明一元函数“连续未必可导”概念

一元函数“连续未必可导”不需要我们写出很复杂的公式，我们只需要看几张图就可以了。

比如， $y=|x|$ 的图像如下所示：

其导数如下所示：

从上面的分析中，我们知道， $y=|x|$ 的图像显然是连续的（这个肉眼可见，无需证明），但是在尖点处（x=0点处）是不可导的，因为它的左导数是-1，右导数是1。

所以，当函数出现了尖点，那么它的导数就不存在了，尽管函数在尖点处是连续的。而像这样的函数多了去了，比如：

再比如：

这个函数在该点的切线是垂直的，所以导数值是无穷的，但是导数值等于无穷并不是导数存在的一个情况。

问：为什么在尖点处函数不可导？

答：因为在尖点处，左右两侧函数图像在这个点处的切线斜率是不同的，也就是函数在该点的左导数和右导数不相等，所以函数在尖点处不可导。

以上就是“连续未必可导”的一元函数的情况。

二、二元函数的可偏导和连续

先说结论：二元函数的连续和可偏导没有任何关系。或者说，连续未必可偏导，且可偏导未必连续。

1、证明二元函数的“可偏导未必连续”

在证明这个结论之前，我们先回顾一下关于连续和可偏导的一个小定义：

连续的定义是：极限值等于实际的函数值。如下图所示：

上图表示，函数在某点处的极限定义的区间。简而言之，就是在点 $(x_{0},y_{0})$ 的一个去心邻域里面（就是那个圆圈里必须全都有定义）

比如上面这个函数在(0，0)点就是不连续的，因为如果要连续，那至少要定义函数在（0，0）点的邻域上（即画圈部分）全部都有定义，而实际上却只有蓝线上有定义，也就是只定义了两个路线，并不能满足所有的趋近方式都连续的一个基本原则。所以上图根本就谈不上连续。

但是，上图的偏导数是存在的。我们说过，偏导数其实就是截线的斜率。比如我们要算关于y的偏导数，那就让x=0，那也就是zoy平面了，这个平面截下来就是一根z=1的直线，斜率显然为0。同理，关于x的偏导数也是0，因为也是一根z=1的直线。所以这个函数在点（0，0）处是可偏导的，但是根本就谈不上连续，因为它的定义域不足够让它去谈连续。

2、证明二元函数的“连续未必可偏导”

我们来看下面这个例子：

我们知道，一个不可导的连续函数往往都存在着尖点。上面就是一个多元的连续但不可偏导的图形。

那么这个函数在0点处关于x的偏导数是多少呢？

那么既然是关于x的偏导数，那就让y=0保持恒定呗，如下图：

显然，截取后的图像在0点处是一个尖点，那么也就没有切线。所以它在0点是一个不可偏导的函数。

3、最后总结

多元函数的连续和可偏导是没有任何关系的。

在学习高等数学的时候，一定不能陷入这样一个误区，就是死套概念，背公式。这样是不行的。一定要进行数形结合，然后脑子里尽量去记一些例子。这样我们的学习才能事半功倍。

视频4（铺垫）：微分（一元函数）

原视频：微分的定义：可微到底在讲啥？_哔哩哔哩_bilibili

“微分”这个概念到底是怎么被定义出来的？它的几何意义到底是在讲什么？下面咱们就来聊聊“微分”。

一、引入

举个例子：

有一个函数 $y=f(x)=3x$ ，在 $x_{0}$ 点处，给自变量 $x_{0}$ 一个小增量 $\Delta x$ ，即变成了 $x_{0}+\Delta x$ ，我想知道因变量 $y$ 的变化，即 $\Delta y$ 是多少。

这个显然很好算，就是： $\Delta y=f(x_{0}+\Delta x)-f(x_{0})=3(x_{0}+\Delta x)-3x_{0}=3\Delta x$

我们可以清楚地看到，这里 $x$ 的增量 $\Delta x$ 和 $y$ 的增量 $\Delta y$ 是呈线性关系的，或者说是呈一次方的关系。这个线性关系显然在每个点都是成立的。

但是，对于任意的函数，自变量和因变量都是这样线性的关系吗？并不是！

再举个例子：

显然，上面这个函数的因变量 $y$ 与自变量 $x$ 的关系就不是线性关系了，而是一个二次方的关系

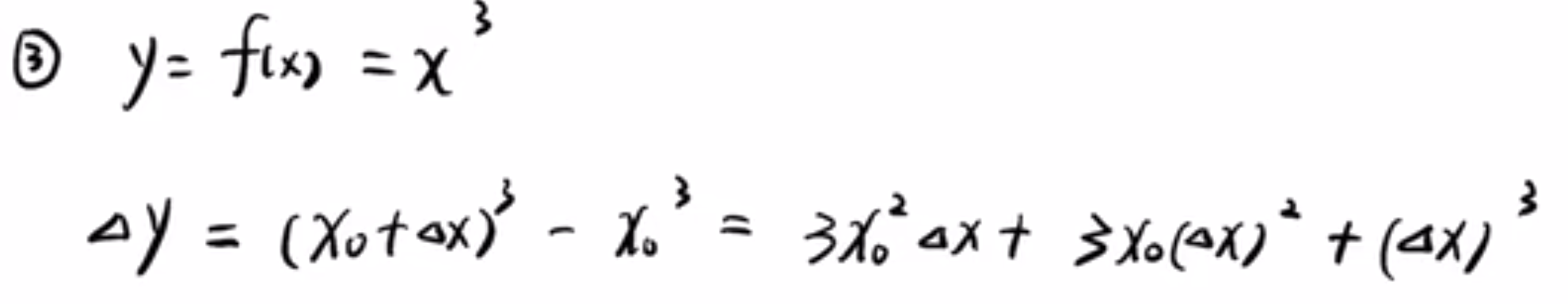
上面这个因变量增量和自变量增量的关系就变成了三次方的关系。

所以，自变量增量和因变量增量的关系并不永远都是线性的。但是，当我的 $\Delta x$ 非常小，小到趋近于0的时候，这些 $(\Delta x)^{2}$ 和 $(\Delta x)^{3}$ 都是高阶无穷小了，几乎就可以忽略掉了。

所以我们就可以根据上面三个式子总结经验，然后可微的定义就出来了：

假如在某一点处， $\Delta x$ 和 $\Delta y$ 满足线性关系， $\Delta y=A\Delta x+o(\Delta x)$ （这里 $o(\Delta x)$ 是关于 $\Delta x$ 的高阶函数，当 $\Delta x\rightarrow 0$ 时， $o(\Delta x)$ 时关于 $\Delta x$ 的高阶无穷小，几乎可以忽略掉）。由此可得，上面三个例子可化简为：

（1） $\Delta y=3\Delta x$

（2） $\Delta y=2x_{0}\Delta x+o(\Delta x)$ （其中 $x_{0}$ 是常数， $o(\Delta x)=(\Delta x)^{2}$ ）

（3） $\Delta y=3x_{0}^{2}\Delta x+o(\Delta x)$ （其中 $x_{0}$ 是常数， $o(\Delta x)=3x_{0}(\Delta x)^{2}+(\Delta x)^{3}$ ）

综上所述，如果函数在某一点处满足 $\Delta y=A\Delta x+o(\Delta x)$ （这里 $o(\Delta x)$ 是关于 $\Delta x$ 的高阶函数，当 $\Delta x\rightarrow 0$ 时， $o(\Delta x)$ 时关于 $\Delta x$ 的高阶无穷小，几乎可以忽略掉）这样一个“类似线性”的关系，就可以认定函数在该点处可微。

1、A到底是什么？

通过前面的讲解我们可以知道，“可微”其实是一个人为定义的概念。那么问题来了，这里的 $A$ 到底是啥呢？？？往下👇看！！！

所以，这里的A其实就是函数在 $x_{0}$ 点处的导数值。

2、微分的几何意义

上面聊了第一个问题，我们知道了 $A$ 其实就是导数。接下来我们来聊聊第二个问题，就是可微的式子到底在讲什么，或者说当 $\Delta y=f^{'}(x_{0})\Delta x+o(\Delta x)$ （注意：这里 $A=f^{'}(x_{0})$ ， $\Delta x\rightarrow 0$ ）这个式子成立的时候，到底意味着什么？

由于 $\Delta x\rightarrow 0$ ， $o(\Delta x)$ 是关于 $\Delta x$ 的高阶无穷小，所以上面的式子可以写成：

$\Delta y=f^{'}(x_{0})\Delta x$

即： $y-y_{0}=f^{'}(x_{0})(x-x_{0})$

而上面这个式子，其实不就是函数 $y=f(x)$ 在 $x_{0}$ 点处的切线方程么！！！

所以，当 $\Delta y=f^{'}(x_{0})\Delta x+o(\Delta x)$ 存在，就意味着在 $x_{0}$ 点处，切线存在。就这么简单！！！

所以同学们会经常看到这样一组关系式：就是在一元微分学里面，可导和可微是完全等价的概念，即：可导 $\Leftrightarrow$ 可微。“可导”意味着函数在该点处的导数存在（导数值就是切线斜率）；“可微”意味着函数在该点处的切线存在。这两者是完全等价的。

所以一元函数在某点处可微的几何意义就是——在该点处存在切线。

3、总结

微分这块我们重点要掌握2个方面：

（1）它是怎么被定义出来的

（2）它的几何意义到底是什么

视频4：全微分（多元函数）

原视频：【多元微分专题4】全微分是什么意思？_哔哩哔哩_bilibili

一、回忆一下微分

上一个视频讲过如下内容：

二、正式讲全微分

那么我们聊完了微分之后，来聊一聊全微分。前面讲过，微分本质上是反映在某点处关于x的增量和关于y的增量之间是否满足一个线性关系。或者说，因变量的增量和自变量的增量是否满足一个线性关系。

我们知道，一个二元函数在 $(x_{0},y_{0})$ 点处，x和y这两个自变量都有可能发生变化，即： $(x_{0}+\Delta x,y_{0}+\Delta y)$ 。

此时， $\Delta z=f(x_{0}+\Delta x,y_{0}+\Delta y)-f(x_{0},y_{0})$ 。这个就是二元函数的因变量z的增量，我们称之为“全增量”。之前在偏导数的视频里我们聊到过“偏增量”，就是让x变但y不变，或者y变但x不变。现在是x和y都发生变化，这就叫做“全增量”。

那么，仿造一元微分的概念，我们也可以定义出二元全微分的概念：

假如因变量的增量和自变量的增量之间满足线性关系，那么就称这个函数在该点处是可微的。表达式如下所示：

这里要稍微解释一下，后面的那个 $o(\Delta x,\Delta y)$ 函数其实是自变量的变化半径。如下图所示：

所以，这里的 $o(\Delta x,\Delta y)$ 也可以直接写成 $r$ ，即：

$\Delta z=A\Delta x+B\Delta y+o(r)$

所以，全微分概念和一元微分概念的长相和形式其实是非常一致的。

接下来，我们来研究两个问题：

1、可微必连续

当函数 $f(x,y)$ 在点 $(x_{0},y_{0})$ 处可微时，那么下面👇的式子就成立

这时，我在左右两天同时让 $\Delta x$ 和 $\Delta y$ 趋近于0，那么此时，右侧的式子就直接为0了，如下👇所示：

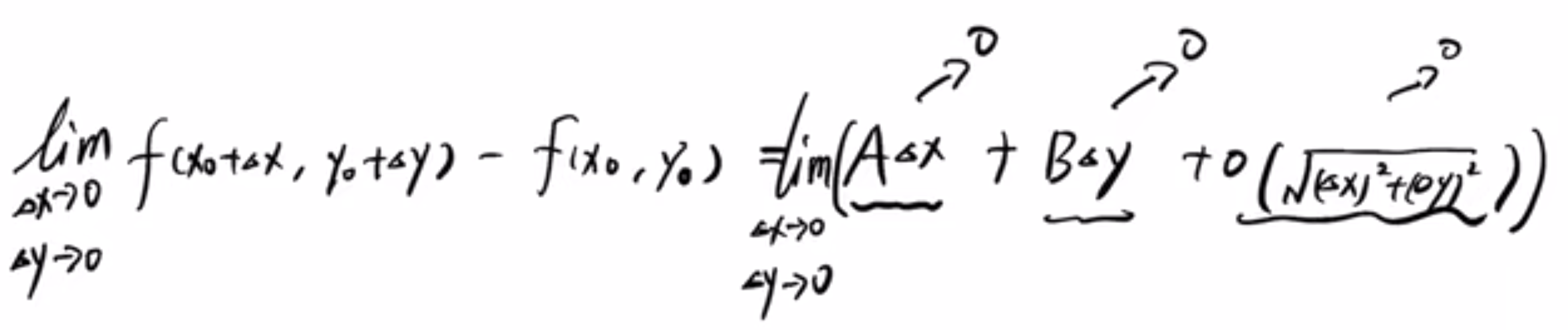
于是，我们就得到了👇：

显然，左边这个式子其实就是函数 $f(x_{0},y_{0})$ 在点 $(x_{0},y_{0})$ 处的极限值。而右边就是函数在该点处的定义值（实际值）

那么一个函数的极限值等于它在该点处的实际值，这不就是函数在该点处连续的定义么！！！

所以，可微必连续。

2、可微必可偏导

首先我们来看一下下面👇这个式子，这个式子是说，当 $\Delta x$ 和 $\Delta y$ 都跑向0的时候，这个式子是成立的。即：在点 $(x_{0},y_{0})$ 处往 $360^{0}$ 方向上的变化都是成立的。

那么请问，这个 $360^{0}$ 的方向，是否包含下面这两个方向？当然是包含的！

那么我们以左边这个图的方向为例，从 $(x_{0},y_{0})$ 变到 $(x_{0}+\Delta x,y_{0})$ 的时候，最上面的式子可以变成：

那么接下来我们在两边同时除以 $\Delta x$ ，并且在两边同时取极限：

显然，左边是函数在点 $(x_{0},y_{0})$ 处关于 $x$ 的偏导数；而右边直接就等于 $A$ 了。即：

$f_{x}(x_{0},y_{0})=A$

所以，当下面👇式子成立的时候，

就可以得到 $A$ 必须等于函数在点 $(x_{0},y_{0})$ 处关于 $x$ 的偏导数；那么同理， $B$ 也必须等于函数在点 $(x_{0},y_{0})$ 处关于 $y$ 的偏导数，如下所示：

所以此时，我不仅证明了“可微必可偏导”，而且还严格证明了“ $A$ 和 $B$ 就分别等于关于x和y的这两个偏导数”。

三、全微分的几何意义

接下来我们来了聊一聊全微分的几何意义。

一个二元函数在某处可微，意味着函数满足如下的关系式（高阶无穷小就省略了哈~）：

只要你仔细看一下，你就会发现，上面这个式子其实就是这个函数在点 $(x_{0},y_{0},z_{0})$ 点处的切平面方程。

四、总结

“一元可微”是说这个函数在该点处存在切线。

“二元可微”意味着这个函数在该点处存在切平面。

以上就是关于全微分的讲解。总结一下，“可微”这个条件在多元函数的微分学里面是一个相当高级的条件。因为可微必然可偏导，可微必然连续。当然，除了记住这些“可微必可偏导、可微必连续”这些概念性的口诀之外，一定不能忽视其推导过程，这个是非常重要的，因为考试是不考口诀的，考试永远都是考原理。这一点大家一定要注意。

视频5：如何判断多元函数的可微性

原视频：【多元微分专题5】如何判断多元函数的可微性_哔哩哔哩_bilibili

在之前的几个视频中，我们聊了多元函数的很多基本概念，比如：可微、连续、可偏导。我们之前有聊过，所谓可微，说白了在几何意义上来讲，就是这个函数比较“圆润”，函数的曲面比较光滑。但是，从数学角度，或者说从考试角度，如何去判断可微呢？总不能去画张图吧？所以本期视频我们就来聊聊可微性到底如何用数学方法来判别。

首先，我们来回顾一下可微的定义：

假如一个多元函数在某个点，它的x和y的增量满足以下关系，那我们就说这个函数在这点处是可微的。

上一期视频我们已经详细解释了这个定义，那么我们该如何判别可微呢？毕竟定义是定义，它说得还是比较模糊的，它说只要你能写出这个式子，但是什么叫写出这个式子？能不能给我一个计算上面的依据？

其实计算上的依据也是非常简单的，我们只要紧紧抓住上面式子的这个高阶无穷小就可以了。

那么我们如何去利用式子中的高阶无穷小？其实非常简单，只要把上面这个式子做一个简单的移项，如下所示：

接下来，我们用两道题来告诉你判别可微该如何去做：

略

视频6：方向导数和梯度

一、回忆偏导数

多元函数（比如有x、y两个变量）在某个点有两个偏导数，一个是关于x的偏导数，一个是关于y的偏导数。如下所示：

关于x的偏导数：就是y不变，看函数关于x的变化率（如下图第一个式子）；

关于y的偏导数：就是x不变，看函数关于y的变化率（如下图第二个式子）。

所谓偏导数，其实就是某点处函数在x的正方向或y的正方向上的变化率。从图像上来看就是上面粉色和绿色的两个平面。

但是，这个点在xy平面上难道就只能向x的正方向或y的正方向去变化吗？显然不是，它是可以向很多方向变化的。由此，就引申出了“方向导数”这个东西。

二、回忆方向余弦

将向量单位化就是：用向量的两个坐标分别除以这个向量的长度。

三、方向导数

下图中，函数在蓝色点(x,y)处对应的值为黑色点(x,y,z)，而蓝色点可以沿着各个方向运动，那么当蓝色点的位置发生变化时，函数上的黑色点的位置也会随之变化。这里就有一个所谓“变化率”的感觉。

那么，我们画成图像就是下面这样：假如xy平面上的点是按照紫色箭头方向变化的，那么毫无疑问，它在函数上就会投影出一段曲线。如下所示⬇️

上图中切线的斜率就是函数在xy平面上那个点沿紫色方向的变化率。

那么，方向导数到底应该怎么定义呢？

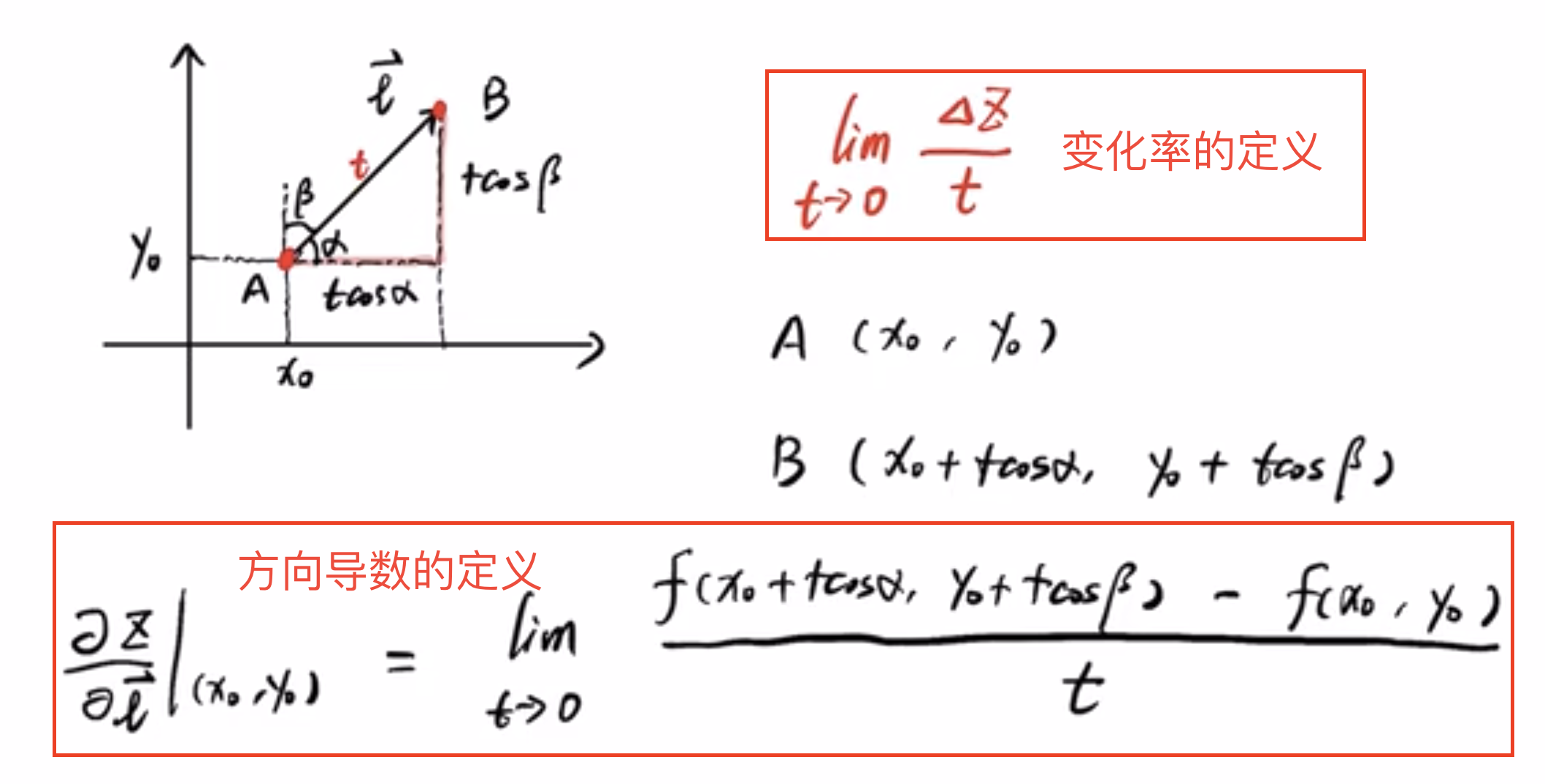
其实，方向导数就是一个变化率。在 $l$ 方向上的变化率说白了就是从A点走了一个非常小的距离t到了B点，即：自变量从A点走到了B点，那么因变量z也会发生一个 $\Delta z$ 的改变。那么变化率就是上图中红字部分的公式。上图中红色框内的公式就是方向导数的定义。

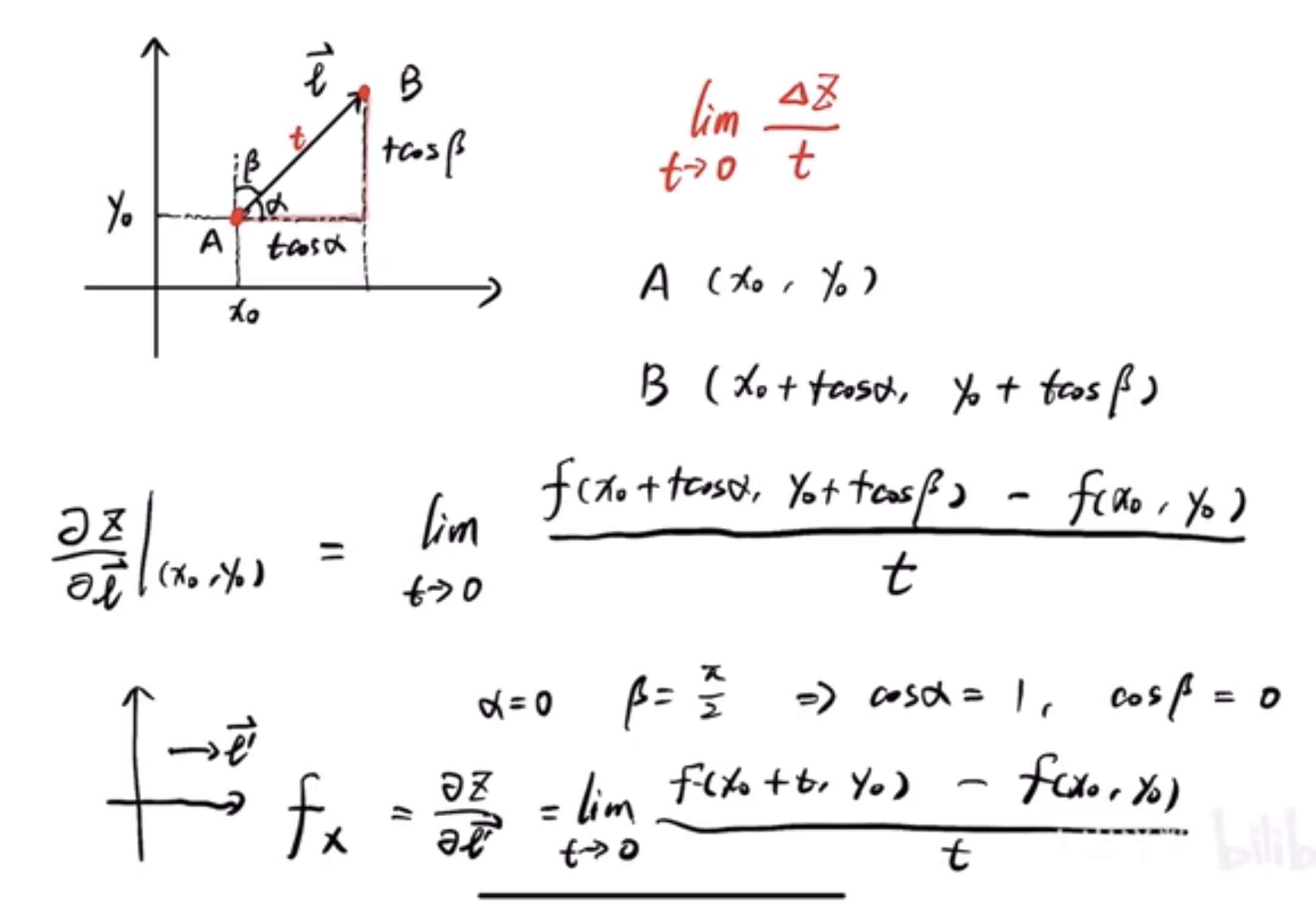
所以，当你知道了方向导数的定义之后，你应该更加深刻的认识到偏导数其实就是方向导数的一个特例。比如x的偏导数就是自变量沿着x轴的正方向的时候，z的变化率。如上图最下面的公式所示，而这，不就是关于x的偏导数么！！！

四、方向导数的计算（需要一个可微的条件）

上面我们讲的是定义式子，方向导数计算必须要求一个可微的条件，因为我们后面的证明中需要这个条件。

首先，我们要记住一个公式：一个函数在某点处的方向导数等于下面👇

所以，方向导数其实和偏导数是息息相关的。

上述公式的证明如下：

该公式必须在可微的情况下才能推导出来。

因为之前我们讲过，在可微的时候，满足以下条件👇

而全微分是在任何一个变化方向上都成立的，当然也包括刚才 $\alpha$ 和 $\beta$ 的方向

例题：

上图👆中 $(u_{x},u_{y},u_{z})$ 这个向量就是传说中的“梯度向量”，也是接下来要讲的内容。毫无疑问，你可以感受到，方向导数和梯度其实是分不了家的。

五、梯度（Gradient）

梯度有下面👇两种写法，都可以，左侧一般是当我们计算函数在某点处的梯度的时候这样写，右侧是以算子的形式写的梯度

上图中右侧的算子形式的梯度等于一个向量👇，即分别关于自变量求偏导，这个向量就是我们的“梯度向量”

其实，计算梯度向量不需要我过多的解释，怎么算其实很简单。那现在问题就是，我们要去理解一下这个梯度向量。

理解一个向量肯定要从两个方面入手：

向量是一个既有大小，又有方向的量。所以我们想知道这个向量的方向是什么，以及这个向量的大小是什么。

为了理解这两个问题，我画了张图👇

从上图中可以看到，所谓的方向导数其实是梯度向量和方向向量去做内积得到的，而这个梯度向量是固定的，我们不管它。但是在某点处我们自变量变化的方向 $l$ 可不一定固定哦，它是 $360^{o}$ 都有可能的，而当 $l$ 指向不同方向的时候，我们的方向导数肯定是不一样的。我们前面也看过图，在不同方向上切线的斜率也是不一样的。

那么现在，我问一个问题，随着 $l$ 的变化，它的方向导数显然是发生变化的，那么请问方向导数什么时候达到最大值呢？

其实我们可以来算一下，方向导数的值=梯度向量的模 $*$ 单位向量的模 $*$ $cos\theta$ ，由于 $l$ 是单位向量，单位向量的模等于1，这样，我们就可以解决两个问题，一是梯度向量的模是多少。梯度向量的模或者说长度是固定的，即： $||\bigtriangledown f||=f^{2}_{x}+f^{2}_{y}$ ，在某个点处这个式子的值当然是固定的了。那么既然它固定了，我们方向导数的变化就只能是根据 $cos\theta$ 来了，而当 $\theta =0$ 时， $cos\theta$ 能取到最大值，这个最大的值就是梯度向量的模。