费曼：数学与物理学的关系

在物理学中，我们需要巴比伦式方法，而不是欧几里得或希腊式方法。

----费曼

对于那些不懂数学的人来说，要真正感受大自然的最深刻的美，是很困难的。

----费曼

在思考数学和物理的应用时可以想到，当复杂的情况涉及到大量数字时，数学很自然会有用。例如，在生物学中，病毒对细菌的作用是不数学的。如果你在显微镜下观察它，一个颤动的小病毒在形状奇特的细菌上找到了一些点——它们都是形状不同的——它可能会把它的DNA推进去，也可能不会。然而，如果我们用数以百万计的细菌和病毒做实验，我们就可以通过取平均值来了解很多关于病毒的知识。我们可以用数学方法求平均值，看看病毒是否在细菌中生长，有什么新的菌株和新菌株的百分比； 所以我们可以研究基因，突变等等。

再举一个简单些的例子，想象一个巨大的棋盘，一个用来下跳棋的棋盘。任何一步的实际操作都不是数学上的——或者说在数学上它非常简单。但你可以想象，在一个巨大的棋盘上有很多很多的棋子，一些对于最佳走法、好棋或坏棋的分析可以通过一种深入的推理来进行，这可能需要有人先进行深入的思考。这就变成了数学，包括抽象推理。另一个例子是计算机的交换。如果你有一个开关，要么开要么关，这没有什么数学意义，尽管数学家喜欢从这里开始他们的数学。但是由于所有的连接和连线，要弄清楚一个非常大的系统会做什么就需要数学。

我想马上说， 数学在物理学中有巨大的应用，特别在讨论复杂情况下的详细现象时，数学使实现基本的规律成为可能。如果我只讨论数学和物理的关系，我会花很多时间来讨论这个问题。但由于这是关于物理定律特性的系列讲座的一部分，我没有时间讨论在复杂情况下会发生什么，但将立即转到另一个问题，即基本定律的特性。

如果我们回到棋盘游戏，基本规则就是棋子移动的规则。数学可以应用在复杂的情况中，以找出在给定的局面下，什么走法是一个好棋。但是，在这里，基本规则的简单基本特征不需要多少数学，它们可以简单地用英语表述。

物理学的奇怪之处在于，对于基本定律，我们仍然需要数学。我会举两个例子，一个我们真的不需要数学，另一个我们需要。首先，物理学中有一个定律叫做法拉第定律，它说在电解过程中，沉积的物质量与电流和电流作用的时间成正比。这意味着沉积的物质量与通过系统的电荷成正比。这听起来很数学，但实际发生的是，穿过导线的每个电子带一个电荷。举个特别的例子，可能要沉积一个原子需要一个电子，所以沉积的原子数必然等于流动的电子数，因此与穿过导线的电荷成正比。因此，这个外表看起来数学的定律没有什么深奥的基础，不需要真正的数学知识。每个原子需要一个电子才能沉淀下来， 这是数学， 但是，我想，这不是我在这里要谈论的数学。

另一方面，以牛顿万有引力定律为例，我给你们这个方程

         

以便让你们对数学符号传递信息的速度产生深刻印象。我说过力与两个物体质量的乘积成正比，与它们之间距离的平方成反比，而且物体对力的反应是改变速度或者改变运动，并且改变在力的方向上，其量与力成正比、与质量成反比。这些话都是对的，我不需要把方程写出来。然而，这是一种数学，我们想知道这怎么能成为基本定律。这个星球会做什么? 它会不会观察太阳，看看离它有多远，然后决定在它内部的加法计算机上计算距离平方的倒数，然后告诉它要移动多少吗? 这当然不是对万有引力机制的解释! 你可能想要看得更远，很多人都试图看得更远。最初有人就他的理论问牛顿:“但它没有任何意义——它没有告诉我们任何东西。”他说:“理论告诉你它是如何移动的。这应该足够了。我只告诉你它是如何移动的，没有告诉你为什么这样。”但是，人们往往不满足于没有一个机制，关于这种你可能想要的机制，我将描述一个已经发明的理论中的一个。这一理论建议这种引力效应是大量作用的结果，这一理论可用以说明引力理论为什么需要是数学的。

假设世界上到处都有很多粒子，它们以很高的速度从我们身上飞过。它们从四面八方均等地飞来——只是匆匆掠过——偶尔还会轰击我们。我们和太阳对它们来说几乎是透明的，但不是完全透明的，有时会被它们击中。那么，看看会发生什么（图1）:

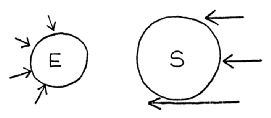
图1

S是太阳，E是地球。如果太阳不在那里，粒子就会从四面八方轰击地球，少数撞击的粒子产生微小的冲击，像砰砰的响声。这不会在任何特定的方向扰动地球，因为从这边来的和从那边来的一样多，从上面来的和从下面来的一样多。然而，当太阳在那里时，从太阳那个方向来的粒子被太阳吸收了一部分，因为其中一些粒子击中了太阳而没有穿过。因此，来自太阳方向的粒子数目比来自其他方向的数目要少，因为它们遇到了一个障碍，即太阳。很容易看出，如果太阳离得越远，则在粒子可能到来的所有方向中，来自太阳方向被去掉的粒子比例就越小。太阳会显得更小——实际上与距离的平方成反比。因此，就会有一个地球向着太阳方向的冲力，该力与距离的平方成反比。这将是大量非常简单的作用的结果，即只是撞击，一个接一个从各个方向的撞击。因此，数学关系的奇异性大大降低了，因为其基本作用要比计算距离平方的倒数简单得多。这个方案是利用粒子撞击来进行计算

   这个方案唯一的问题是，由于其他原因，它不起作用。每一个你创造的理论都必须根据所有可能的结果来进行分析，看看它是否能预测其他东西。这个方案确实预示了一些别的事情。如果地球在运动，从前面撞击地球的粒子会比从后面撞击地球的粒子多。(如果你在雨中跑步，雨水打在你脸前面的比打在后脑勺的要多，因为你在雨中跑步。)所以，如果地球在运动，它就会撞向向着它的粒子，远离从后面追赶它的粒子。所以从正面撞击它的粒子比从背面撞击它的粒子多，所以会有一个力反对任何运动。这种力会使地球在轨道上减速，而且肯定不会使它能保持绕太阳运行30亿年或40亿年(至少)。这个理论就讲到这里。“嗯，”你说 “这是一个很好的理论，我暂时摆脱了数学。也许我可以发明一个更好的。”也许你可以，因为没人知道最终是什么。但直到今天，从牛顿时代开始，还没有人发明出另一种理论来描述这一定律背后的数学机制，这种描述要么重复同样的事情，要么使数学更难，要么预测一些错误的现象。所以，除了数学形式，今天没有引力理论的模型。

如果这是唯一一个具有这种特性的规律， 那就有趣了，而且也让人烦恼。但事实证明，我们研究得越多，发现的规律就越多，我们对大自然的了解越深，这种疾病就越顽固。我们的每一条定律都是相当复杂而深奥的数学表述。牛顿关于万有引力定律的陈述是相对简单的数学。随着我们的深入，它会变得越来越深奥，越来越困难。为什么? 我一点也不知道。我在这里的目的只是要告诉你们这个事实。这次讲座的责任只是要强调这样一个事实: 如果没有对数学的深入理解，就不可能用人们能感受到的方式诚实地解释自然规律的美。我很抱歉，但情况似乎就是这样。

你可能会说，‘好吧，如果没有对于规律的解释，至少告诉我规律是什么。为什么不用文字代替符号告诉我呢? 数学只是一种语言，我希望能够翻译这种语言。”事实上，只要有耐心，我就能做到，我想我在一定程度上做到了。我可以进一步更详细地解释，这个方程意味着，如果距离是两倍，则力是四分之一，以此类推。我可以把所有的符号转换成文字。换句话说，当外行们都坐在那里满怀希望地等着我解释一些事情时，我可以友好地对待他们。不同的人因为其用外行的语言向外行解释这些困难而深奥问题的技能而有不同的名声。外行会一本书接一本书地寻找，希望能够避免最终出现的复杂问题，即使有了最好的解释者也不例外。当他读下去的时候，他发现自己越来越困惑，一个又一个复杂的陈述，一个又一个难以理解的东西，所有这些显然都是彼此无关的。事情变得模糊，他希望也许在其他一些书中会有一些解释.......这个作者还差一点——也许另一个作者会说对。

但我不认为这是可能的，因为数学不仅仅是另一种语言。数学是一种加上推理的语言; 它就像语言加上逻辑。数学是推理的工具。事实上，它是一些人仔细思考和推理的结果的一个大汇总。从数学上讲，可以把两种陈述联系起来。例如，我可以说这个力是指向太阳的。我还可以告诉你，就像我做的那样，行星的运动是这样的，如果我画一条从太阳到行星的线，然后在某个特定的时期，比如三周后，再画一条线，那么行星围绕太阳旋转时扫过的面积严格等于它在接下来的三周内扫过的面积， 以及在再接下来的三周内扫过的面积，等等。我可以仔细地解释这两种说法，但我不能解释为什么它们都是一样的。自然界表面上的巨大复杂性，以及它所有的每一个都已经仔细地向你解释过的有趣的法则和规则，实际上是非常紧密地交织在一起的。然而，如果你不懂得数学，你就看不出逻辑允许你在千变万化的事实中从一个到达另一个。

令人难以置信的是，我可以证明，如果力指向太阳，在相等时间内将扫出相等的面积。如果可以的话，我将做一个演示来向你们展示这两件事是等价的，这样你们就能欣赏到这不仅仅是关于两个定律的陈述。我要证明这两个定律是联系在一起的，所以仅仅是推理就能把你从一个引向另一个，而数学就是有组织的推理。然后你就会欣赏到这些陈述之间的关系的美。我要证明这个关系，即如果力指向太阳，在相等时间内将扫出相等的面积。

图2

我们从一个太阳和一个行星(图2)开始， 我们想象在某一时刻， 行星位于位置1。它以这样的方式移动，比如说，一秒钟后它移动到位置2。如果太阳没有对地球施加一个力，那么，根据伽利略的惯性原理，它会沿着一条直线继续运动。所以在相同的时间间隔后，下一秒，它会在同一条直线上移动相同的距离，到位置3。首先我们要证明，如果没有力，那么在相等时间内将扫出相等的面积。我要提醒大家三角形的面积是底的一半乘以高度， 高度就是到底的垂直距离。如果三角形是钝角(图3)， 那么高度是垂直高度AD，底是BC。现在让我们比较一下如果太阳不施加任何力时将被扫出的面积(图2)。

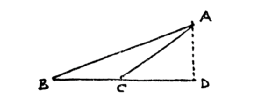
图3

记住，1-2距离和2-3距离是相等的。问题是， 这两个面积相等吗? 考虑由太阳和点1和2组成的三角形。它的面积是多少? 它是以1-2为底，乘以从基线到S的垂线高度的一半。另一个三角形呢，从2运动到3的三角形? 它的面积是底2-3乘以到S的垂线高度的一半。这两个三角形高度相同，而且，正如我指出的，底相同，因此它们的面积相同。到目前为止一切顺利。如果没有来自太阳的力，在相同时间内将会扫出相同的面积。但是有一种来自太阳的力。在间隔1-2-3期间，太阳在不同的方向上拉动并改变运动。为了得到一个很好的近似值，我们将取2处为中心位置或平均位置，并假设在间隔1-3期间的整个效果是在直线2-S方向上以一定的数量改变运动(图4)。

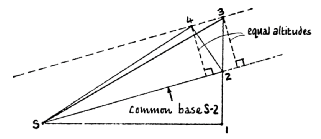
图4

   这意味着，虽然质点在直线1-2上运动，而且如果没有力，会在下一秒继续在同一直线上运动，但由于太阳的影响，它们的运动被一个与直线2-S方向平行的戳动一下的量所改变。因此，下一个运动是行星想要做的事和太阳作用引起的变化的复合。所以行星最终不是在位置3，而是在位置4。现在我们要比较三角形23S和24S的面积，我将向你们展示它们是相等的。它们有相同底S-2。它们的高度相同吗? 当然，因为它们包含在两条平行线之间。4到直线S-2的距离等于3到S-2延伸直线的距离。因此三角形S24的面积等于三角形S23的面积。我之前证明了S12和S23的面积相等，所以我们现在知道S12 = S24。所以，在行星的实际轨道运动中第一秒和第二秒扫过的面积是相等的。因此，通过推理，我们可以看到力朝向太阳的这一事实与面积相等这一事实之间的联系。 这不是很巧妙吗? 这些我是直接从牛顿那里借来的。它直接来自于《原理》，包括图等等。只有字母不同，因为他是用拉丁文写的，而这些是阿拉伯数字。

   牛顿在他的书中把所有的证明都做成几何形式。今天我们不使用这种推理。我们使用符号作一种分析推理。使用几何方法需要精巧地画出正确的三角形、注意到面积的关系，并且需要弄清楚如何做到这些。但是，使用分析方法已经对此有所改进，分析方法速度更快、效率更高。我想展示一下使用现代数学的符号的分析是什么样子的，你其他什么都不用做，只需要写很多符号就能算出来。

我们想要讨论面积变化的快慢，我们用Ȧ表示。面积随半径摆动而变化，与半径成直角的速度分量乘以半径，告诉我们面积变化的快慢。所以这是径向距离乘以速度（或者说距离的变化率）这个乘积的分量。

现在的问题是面积的变化率本身是否变化。原理是，面积的变化率不应该改变。所以我们再微分一次，这意味着一些关于把点放在正确位置的小技巧，就这些。你必须学会这些技巧; 这只是人们发现的对这种事情非常有用的一系列规则。我们写:

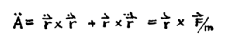
第一项表示取速度在与其成直角处的分量。它是零，这是因为速度与自身方向相同。加速度，就是二阶导数，r加上两点，或者说速度的导数，就是力除以质量。

这就是说面积变化率的变化率是力在与半径成直角方向的分量，但如果力是沿半径方向的

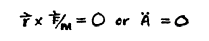
就像所牛顿说的那样，那么就没有与半径成直角的力，这就意味着面积的变化率不变。这仅仅说明了使用不同种类符号的分析的力量。牛顿或多或少知道怎么做，只是用了不同的符号; 但他把所有东西都写成几何形式，因为他想让人们能读懂他的论文。他发明了微积分，也就是我刚才展示的那种数学。

这很好地说明了数学与物理的关系。当物理问题变得困难时，我们通常会求助于数学家，他们可能已经研究过这类问题，并为我们准备了一套推理方法。另一方面，他们可能没有，在这种情况下，我们必须发明我们自己的推理路线，然后我们把它传回给数学家。每一个仔细对任何事物作思考和推理的人都在为你所思考的事物的知识做出贡献，如果你把它抽象出来，送到数学系，他们会把它作为数学的一个分支写进书里。数学就是一种从一组命题转换到另一组命题的方法。它在物理学中显然是有用的，因为我们有这些不同的方法来谈论事物，而数学允许我们发展结果，分析情况，并以不同的方式改变定律来连接各种命题或陈述。事实上，物理学家所知道的总量是非常少的。他只需要记住从一个地方到另一个地方的规则，他就没问题了，因为所有关于相等时间的陈述，力在半径方向上等等，都可以通过推理联系在一起。

现在出现了一个有趣的问题。可不可以从一个地方开始演绎出所有成果? 自然界中是否存在某种特定的模式或秩序，使我们能够理解到一组陈述是更基本的，而另一组陈述是作为结果的? 有两种看待数学的方式，为了这个演讲的目的，我称之为巴比伦传统和希腊传统。在巴比伦式的数学学校里，学生们通过做大量的例子来学习一些东西，直到他掌握了一般的规则。他还懂得很多几何知识，例如，圆的很多性质，毕达哥拉斯的定理， 立方体和三角形的面积公式; 此外，还有某种程度的论证，以从一个东西到达另一个东西。他们还有了数量表，以致于他们可以求解复杂的方程。一切都是为做计算做准备。但欧几里得发现有一种方法，可以根据一组特别简单的公理将所有的几何定理都排列出秩序。巴比伦人的态度——或者我称之为巴比伦数学——是你知道所有各种各样的定理和它们之间的许多联系，但你从来没有完全意识到这一切都可以都来自一些公理。最现代的数学，在一个什么是可接受的公理、什么不可接受为公理的非常明确的框架内，聚焦于公理和证明。现代几何学采用类似欧几里得公理的东西，加以改进，使之更加完美，然后展示这个系统的演绎。例如，像毕达哥拉斯那样的定理(由直角三角形的直角两边做出的正方形的面积之和等于由斜边做出的正方形的面积)是不可能被认为是公理的。另一方面，从几何学的另一个角度，即笛卡尔的角度来看，毕达哥拉斯定理是一个公理。

我们必须接受的第一件事是，即使在数学中你也可以从不同的地方开始。如果所有这些不同的定理都是通过推理联系在一起的，那么就没有真正的方法来说明“这些是最基本的公理”，因为如果你被告知一些不同的东西，你也可以使推理以另一种方式进行。它就像一座有很多部件的桥，而且它是过度连接的; 如果一部分部件掉了，你可以用另一种方式重新连接。今天的数学传统是从一些特定的想法开始，这些特定想法被某种惯例选择为公理，然后从那里建立结构。我所说的巴比伦思想是说：‘我碰巧知道这个，我碰巧知道那个，也许我知道那个; 然后我从这里开始，把所有东西都做出来。明天我可能会忘记这是真的，但我会记住另一件事是真的，这样我就可以重新构建这一切。我从来不能肯定我应该从哪里开始，又应该从哪里结束。我只是一直记得足够多的东西， 这样当记忆消失，一些碎片掉下来的时候， 我每天都能把它们重新拼起来。‘

总是从公理出发的方法在获得定理时的效率不太高。在几何学中，如果你每次都要从公理开始，那么你的效率就会很低。如果你必须记住几何上的一些东西，你总能从别的地方得到，但是用另一种方法要有效得多。决定哪些是最好的公理并不一定是在一个领域中工作的最有效方法。在物理学中，我们需要巴比伦式方法，而不是欧几里得或希腊式方法。我想解释一下原因。

欧几里得方法的问题是让公理变得更有趣或更重要。但是，例如在万有引力的情况中，我们要问的问题是: 说力是朝向太阳的，还是说在相等时间内扫过相等的面积，是更重要、更基本，或是更好的公理? 从一个角度来看，使用力的表述更好。如果我指出力是什么，我就能处理一个有很多质点的系统，其中轨道不再是椭圆， 因为力的表述告诉我一个质点对另一个质点的拉力。在这种情况下， 关于等面积的定理不成立。因此，我认为力的定律应该是一个公理，而另一个不是公理。另一方面，在有大量质点的系统中，等面积原理可以推广到另一个定理。这说起来相当复杂，而且不像最初关于等面积的说法那么漂亮，但显然它是其产物。以一个有大量质点的系统为例，这个系统可能是木星、土星、太阳和许多星星，它们都相互作用，从远处观察这个系统投射到一个平面上(图5)。 这些质点都在向不同的方向运动，我们取任意一个点，计算从这一点到每个质点的半径扫出的面积。在这种计算方法中，质量越重，分量越重; 如果一个质点是另一个质点的两倍重，那么它扫出的面积也会是另一个质点的两倍。所以我们计算每一个与相应质点质量成比例的扫出面积，把它们加在一起，得到的总数不随时间变化。这个总和叫做角动量，这叫做角动量守恒定律。守恒只是意味着它不会改变。

图5

这一定律的后果之一如下。想象一下，许多恒星落在一起形成了一个星云或星系。起初，它们离中心很远，距离中心的半径很长，移动缓慢，只产生少量的面积。当它们靠近中心时，到中心的距离就会缩短，所以为了每秒产生相同的面积，它们必须移动得更快。你会看到，当恒星进入中心时，它们会越来越快地摆动和旋转，因此我们可以大致了解旋涡星云的定性形状。同样地，我们可以理解滑冰运动员如何旋转。他开始时伸出腿，慢慢地运动，当他把腿收回时，他旋转得更快。当他的腿在外面的时候，它每秒贡献一定的面积，然后当他的腿在里面的时候，他必须旋转得更快才能产生同样的面积。但我没有为滑冰运动员证明这一点， 因为滑冰运动员使用肌肉力量，而重力是另一种力量。但对滑冰运动员来说这是真的。

现在我们有一个问题。我们通常可以从物理学的某一部分（比如万有引力定律）开始作推理，导出一个个比推导结果实际上更加普遍的原理。这在数学中不会发生; 定理不会出现在不应该出现的地方。换句话说，如果我们说物理的假设是引力的等面积定律，那么我们就可以推导出角动量守恒，但这只适用于引力。然而我们在实验中发现，角动量守恒的适用范围要广得多。牛顿还有其他的假设，通过这些假设他可以得到更一般的角动量守恒定律。但这些牛顿定律是错误的。没有力，都是胡扯，质点也没有轨道，等等。但是，关于面积和角动量守恒原理的准确的类比改造，是正确的。它适用于量子力学中的原子运动，据我们所知，它在今天仍然是准确的。我们有这些广泛的原理，它们通行于不同的定律，如果我们过于认真地对待推理，认为一个是有效的，只是因为另一个是有效的，那么我们就不能理解物理学不同分支之间的相互联系。有一天，当物理学完成了，我们知道了所有的规律，我们也许可以从一些公理开始，毫无疑问有人会想出一种特殊的方法，这样就可以演绎推导出其他的一切。但是，虽然我们不知道所有的规律，我们可以使用其中一些来猜测超出了可证范围的定理。为了理解物理学，一个人必须始终保持一种平衡，把所有不同的命题及其相互关系都记在脑子里，因为这些定律往往超出了它们的推论范围。只有知道了所有的定律之后，这一点才不重要。

在数学和物理的关系中，另一件非常奇怪的有趣的事情是，通过数学论证，你可以证明，从许多明显不同的起点出发，却可以得到相同的结果。这是很明显的。如果你有公理，你可以另外用一些定理代替公理; 但实际上，物理定律的构造是如此精巧，以至于它们的不同但等价的表述具有如此不同的性质，这使得它们非常有趣。为了说明这一点，我将以三种不同的方式阐述万有引力定律，它们都完全等价，但听起来完全不同。

第一个表述是物体之间存在力，根据我之前给你们的方程。

每一个物体，当它感受到作用在它上面的力时，就会以每秒一定的数量加速或改变它的运动。这是描述这个定律的常规方式，我称之为牛顿定律。这个陈述说的是，力依赖于有限距离外的某物。它具有我们所说的非局域特性。作用在一个物体上的力依赖于一段距离外另一个物体的位置。

你可能不喜欢超距作用的想法。这个物体在这里怎么可能知道那里发生了什么? 所以还有另一种表述定律的奇怪方法，叫做场的方法。这很难解释，但我想给你一个大概的印象。它说的是一个完全不同的事情。在空间的每一点上都有一个数字(我知道它是一个数字，而不是一个机制: 这是物理带来的烦恼，它必须是数学的)， 当你从一个地方到另一个地方，这个数字就会改变。如果把一个物体放在空间中的一点上，作用在它上的力就是在这个数字变化最快的方向上(我给它一个通常的名字，势能，力就在势能变化的方向上)。此外，力与你移动时势能变化的快慢成正比。这是陈述的一部分，但还不够，因为我还没有告诉你们如何确定势的变化方式。我可以说势与物体之间的距离成反比，但这又回到了超距作用的概念。你可以用另一种方式表述这个定律，它说你不需要知道小球以外的任何地方发生了什么。如果你想知道一个球中心的势能是多少，你只需要告诉我球表面的势能是多少，不管它有多小。你不需要看外面，你只需要告诉我它在附近是多少，以及球的质量是多少。规则是这样的。中心点的势能等于，球表面势能的平均值，减去同样的常数G（就像我们在另一个方程中有的那个常数）除以球的半径(我们称之为a)的两倍然后乘以球内部的质量，如果球足够小的话。

你会发现这个定律不同于另一个定律，因为它是根据附近发生的事情来描述某一点发生的事情。牛顿定律用一个时刻发生的事情来表述另一时刻发生的事情。它给出了如何从一个瞬间到另一个瞬间做出计算，但在空间中它从一个地方跳到另一个地方。第二种陈述在时间上和空间上都是局部的，因为它只取决于附近的东西。但这两种陈述在数学上是完全等价的。

还有另一种完全不同的表述方法，其在哲学和定性观念上都有所不同。如果你不喜欢超距作用，我已经向你展示了你可以去掉它。现在我想给你们展示一个从哲学上完全相反的陈述。在这里，完全没有讨论事物如何从一个地方到另一个地方; 整体包含在一个总体的陈述中，如下所示。当你有很多质点，你想知道一个质点如何从一个地方移动到另一个地方，你可以通过发明一个在给定的时间内从一个地方到达另一个地方的可能运动来实现 (图6)。假设质点想在一小时内从X到Y，你想知道它可以走哪条路线。你要做的就是造出各种曲线，并在每条曲线上计算一个特定的量。(我不想告诉你们这个量是多少，但对于那些听说过这些术语的人，每条路径上的量是动能和势能之差的平均值)如果你为一条路径计算这个数量，然后为另一条计算，你会得到每个路径有一个不同的数值。然而，有一种路径给出的数值最少，那就是质点在自然界中实际走的路线! 我们现在通过描述整个曲线来描述实际的运动，例如椭圆。我们已经失去了因果关系的概念，即质点感受到拉力并根据拉力运动。相反，它以某种宏大的方式嗅出所有的曲线，所有的可能性，并决定选择哪一条(通过选择我们的量最少的那条)。

图6

这是描述自然的广泛优美方式的一个例子。当人们说自然必然有因果关系时，你可以用牛顿定律; 或者，如果他们说，自然必须用一个最小原则来表述，你可以用最后一种方式来谈论它; 或者如果他们坚持认为自然必须有一个局部场——当然，你可以这样做到。问题是: 哪一个是正确的? 如果这些不同的选择在数学上并不完全等价，如果某些选择的结果与其他选择的结果不同，那么我们所要做的就是进行实验，找出大自然实际上选择的是哪种方式。人们可能会来到这里，哲学式地争辩说，他们喜欢这个胜过喜欢那个; 但我们从许多经验了解到，所有关于自然将会做什么的哲学直觉都是失败的。人们只需要计算出所有的可能性，并尝试所有的选择。但在我所讨论的特定情况，理论是完全等价的。在数学上，牛顿定律、局域场的方法和最小值原理这三种不同的表述给出了完全相同的结果。那我们该怎么办? 你将在所有的书中读到，我们不能以合乎科学的方法断定其中的一个或另一个。这是真的。它们在科学上是等价的。不可能做出这样一个判断，因为如果所有的结果都相同，就没有实验方法来区分它们。但从心理上看，他们在两方面有很大不同。首先，从哲学上讲，你喜欢或者不喜欢他们; 训练是战胜这种疾病的唯一途径。其次，在心理上它们是不同的，因为当你试图猜测新的规律时，它们是完全不等价的。

只要物理学是未完成的，我们还在努力理解其他规律，那么不同的可能表述就可能为在其他情况下可能发生的事情提供线索。在这种情况下，它们向我们建议，在更广泛的情况下那些规律可能是什么样子，它们在心理学上就不再是等同的了。举个例子，爱因斯坦意识到电信号的传播速度不可能超过光速。他猜想这是一个普遍的原理。(这就像把角动量从你已经证明过的一种情况推广到宇宙的其他现象的猜谜游戏一样。)他猜想一切事物都是这样，他猜想万有引力也会是这样。如果信号的速度不能超过光速，那么描述瞬时力的方法就很差了。因此，在爱因斯坦对万有引力的概括中，牛顿描述物理的方法是完全不充分的，而且非常复杂，而场方法是简洁的，最小值原理也是如此。我们还没在后两者中挑选出哪个更好。

事实上，在量子力学中，这两种方法都不是我所描述的那样正确的，但最小值原理的存在事实上是粒子在小尺度服从量子力学这一事实的结果。就目前的理解而言，最好的规律实际上是两者的结合，即我们使用最小原理和局域定律。目前我们认为物理定律必须有局域特性，也必须有最小原理，但我们并没有真正知道那是什么。如果你有一个只是部分准确的结构，有些东西会失败，那么如果你用恰当的公理来写它，也许只有一个公理失败，其余的仍然存在，你只需要改变一件小事。但是如果你用另一组公理来写，它们可能都崩溃了，因为它们都依赖于一个失败的东西。如果没有某种直觉，我们无法提前判断，为了发现新情况哪种做法是最好的。我们必须在头脑中始终保持看待事物的所有不同方式; 所以物理学家们只做巴比伦式的数学，很少关注从固定的公理出发做严密的推理。

大自然的一个惊人特征是有各种可能的解释方案。事实说明，只是因为规律是如此特殊和微妙，这才是可能。例如，定律是平方反比的允许它成为局域的; 如果它是立方反比，就不能这样做到了。在方程的另一端，力与速度的变化率有关这一事实允许用最小原理的方式来描述定律。例如，如果力正比于位置的变化率而不是速度的， 那么你就不能这样写。 如果你修改定律太多，你会发现你只能用更少的方法来编写它们。我总觉得这很神秘，我不明白为什么正确的物理定律似乎可以用如此多种多样的方式来表述。它们似乎能同时通过好几个门。

关于数学与物理的关系，我想讲一些比较一般的东西。数学家只是在处理推理的结构，他们并不真正关心他们在谈论什么。他们甚至不需要知道他们在谈论什么，或者如他们自己所说，不需要知道他们所说的是否真实。我会解释的这个。你陈述公理，某某是如此，某某是如此。然后什么? 逻辑可以在不知道某某词的意思的情况下进行。 如果关于公理的陈述是精心制定的， 并且足够完整，那么对于正在进行推理的人来说，为了用同一种语言推理出新的结论，就不需要对词语的含义有任何了解。如果我在其中一个公理中使用了三角形这个词，结论中就会有一个关于三角形的陈述，而做推理的人可能不知道三角形是什么。但我可以把他的推理读回来说，‘三角形，那只是一个有三个边的什么什么'，然后我知道他的新事实。换句话说，如果你有一组关于现实世界的公理，数学家准备好了可以使用的抽象推理。但是物理学家说的每一句话都有含义。这是很重要的一点，很多通过数学学习物理的人都不理解这一点。物理不是数学，数学也不是物理。一个帮助另一个。但在物理学中，你必须理解文字与现实世界的联系。最后，有必要把你已经弄明白的东西翻译成语言，翻译到现实世界中，翻译到你要做实验的铜块和玻璃块中。只有这样你才能知道结果是否真实。这个问题根本不是数学的问题。

很明显，对于物理学家来说，已经发展起来的数学推理当然具有巨大的力量和用处。另一方面，物理学家的推理对数学家有时是有用的。

数学家喜欢使他们的推理尽可能一般化。如果我对他们说:“我想讨论普通的3维空间”， 他们会说:“如果你有一个n维的空间，那么这就是定理。”'但我只想要3的情况'，'好吧，代入n = 3' ! 结果是，很多复杂的定理在应用到特殊情况时就简单多了。物理学家总是对特殊情况感兴趣; 他对一般情况从不感兴趣。他在谈论具体的什么; 他不是抽象地谈论任何事情。他想在三维空间里讨论万有引力定律; 他不想要n维空间中的任意力。所以一定程度的简化是必要的，因为数学家已经为广泛的问题准备了这些东西。这是非常有用的， 后来可怜的物理学家总是不得不回来说：“不好意思，当你想告诉我4维的时候……”

当你知道你在谈论什么时，你知道一些符号代表力，另一些代表质量、惯性等等， 然后你就可以使用很多常识、对世界的直观感觉。你已经看到了各种各样的东西，你或多或少知道这种现象将如何表现。但是可怜的数学家把它翻译成方程，因为符号对他来说没有任何含义，除了数学的精确严密和论证的谨慎之外，他在论证中没有任何向导。物理学家，他们或多或少知道答案是如何出来的，可以部分地猜测，所以可以很快地进行下去。高度准确的数学严密在物理学中没有多大用处。但人们不应该在这一点上批评数学家。没有必要仅仅因为某些东西对物理学有用，他们就必须那样做。他们在做自己的工作。如果你想要别的，那就自己想办法吧。

下一个问题是，当我们试图猜测一个新规律时， 我们是否应该使用直观感觉和哲学原则——“我不喜欢最小原则”， 或“我确实喜欢最小原则”，“我不喜欢超距作用”，或者“我确实喜欢超距作用”。模型在多大程度上有帮助? 有趣的是，通常模型确实有帮助，大多数物理老师都试图讲授如何使用模型，并使人对事物如何运作有一个良好的物理感觉。但事实证明， 最伟大的发现总是脱离了模型而作抽象， 而模型从来没有任何好处。麦克斯韦发现的电动力学首先使用了许多空间中假想的轮子和惰轮。但是当你摆脱了所有惰轮以及空间中的那些东西， 事情就好了。 狄拉克仅仅通过猜测方程就发现了相对论量子力学的正确规律。猜测方程式的方法似乎是猜测新规律的一种相当有效的方法。这再次表明，数学是表达自然的一种深刻的方式，任何企图用哲学原理或凭借机械的直观感觉来表达自然的方法都不是有效率的方法。

根据我们今天所理解的规律，无论一个空间区域多么小，无论一个时间区域多么小，计算机都需要进行无数次逻辑运算才能弄清楚发生了什么， 这一直困扰着我。在这么小的空间里怎么可能发生所有这些事? 为什么要用无限多的逻辑运算来计算一小块空间/时间会做什么呢? 因此，我经常假设，物理学最终不需要数学的陈述，最终机制将被揭示出来，规律将被证明是简单的，就像跳棋盘上的所有表面上复杂的东西一样。但这种猜测和其他人的猜测——“我喜欢它”，“我不喜欢它”——是一样的，对这些抱有太多偏见是不好的。

总结一下， 我想借用金斯说过的话：“伟大的建筑师似乎是位数学家”。对于那些不懂数学的人来说，要真正感受大自然的最深刻的美，是很困难的。斯诺谈到了两种文化。我真的认为，这两种文化把对数学有理解的人和对数学没有足够理解的人在鉴赏大自然上区分开来。

这太糟糕了，它必须是数学，而数学对一些人来说很难。据说——我不知道这是不是真的——一位国王试图向欧几里得学习几何，他抱怨太难了。欧几里得说过，在几何学上没有平坦的大道。世上无坦途。物理学家无法将其转换成任何其他语言。如果你想了解自然，欣赏自然，就有必要了解她的语言。她只以一种形式提供她的信息; 我们还不至于如此的不谦逊，不对其作任何关注就要求她做出改变。

你所能提出的所有理智论证都无法告知聋人音乐体验的真正含义。同样地，世界上所有的理智论证都不能把对自然的理解传达给那些具有“另一种文化”的人。哲学家可能试图通过定性地告诉你自然来教导你。我正在试着描述她。但这没有被做到，因为这是不可能的。也许正是因为他们的眼界受限于此，以至于一些人会想象宇宙的中心是人。

编者按：

本文内容为费曼于1964年所作的一个演讲，收录于《The character of physical law》一书, 本文根据英文版翻译，编译: 廖玮。

文中所说的模型大体接近于机械模型，例如麦克斯韦的以太电磁介质模型，物理学中的模型概念更加广泛，不局限于机械模型。

附录： 英文原文

The Relation of Mathematics to Physics

Richard Feynman

In thinking out the applications of mathematics and physics, it is perfectly natural that the mathematics will be useful when large numbers are involved in complex situations. In biology, for example, the action of a virus on a bacterium is unmathematical. If you watch it under a microscope, a jiggling little virus finds some spot on the odd shaped bacterium- they are all different shapes - and maybe it pushes its DNA in and maybe it does not. Yet if we do the experiment with millions and millions of bacteria and viruses, then we can learn a great deal about the viruses by taking averages. We can use mathematics in the averaging, to see whether the viruses develop in the bacteria, what new strains and what percentage; and so we can study the genetics, the mutations and so forth.

To take another more trivial example, imagine an  enormous board, a chequerboard to play chequers or draughts. The actual operation of any one step is not  mathematical - or it is very simple in its mathematics. But you could imagine that on an enormous board, with lots and lots of pieces, some analysis of the best moves, or the good moves or bad moves, might be made by a deep kind of reasoning which would involve somebody having gone off first and thought about it in great depth. That then becomes mathematics, involving abstract reasoning.  Another example is switching in computers. If you have one switch, which is either on or off, there is nothing very  mathematical about that, although mathematicians like to start there with their mathematics. But with all the interconnections and wires, to figure out what a very large system will do requires mathematics.

I would like to say immediately that mathematics has a tremendous application in physics in the discussion of the detailed phenomena in complicated situations, granting the fundamental rules of the game. That is something which I would spend most of my time discussing if I were talking only about the relation of mathematics and physics. But since this is part of a series of lectures on the character of physical law I do not have time to discuss what happens in complicated situations, but will go immediately to another question, which is the character of the fundamental laws.

If we go back to our chequer game, the fundamental laws are the rules by which the chequers move. Mathematics may be applied in the complex situation to figure out what in given circumstances is a good move to make. But very little mathematics is needed for the simple fundamental character of the basic laws. They can be simply stated in English for chequers.

The strange thing about physics is that for the fundamental laws we still need mathematics. I will give two examples, one in which we really do not, and one in which we do. First, there is a law in physics called Faraday's law, which says that in electrolysis the amount of material which is deposited is proportional to the current and to the time that the current is acting. That means that the amount of material deposited is proportional to the charge which goes through the system. It sounds very mathematical, but what is actually happening is that the electrons going through the wire each carry one charge. To take a particular example, maybe to deposit one atom requires one electron to come, so the number of atoms that are deposited is necessarily equal to the number of electrons that flow, and thus proportional to the charge that goes through the wire. So that mathematically-appearing law has as its basis nothing very deep, requiring no real knowledge of mathematics. That one electron is needed for each atom in order for it to deposit itself is mathematics, I suppose, but it is not the kind of mathematics that I am talking about here.

On the other hand, take Newton's law for gravitation, which has the aspects I discussed last time. I gave you the equation:

just to impress you with the speed with which mathematical symbols can convey information. I said that the force was proportional to the product of the masses of two objects, and inversely as the square of the distance between them, and also that bodies react to forces by changing their speeds, or changing their motions, in the direction of the force by amounts proportional to the force and inversely  proportional to their masses. Those are words all right, and I did not necessarily have to write the equation. Nevertheless it is kind of mathematical, and we wonder how this can be a fundamental law. What does the planet do? Does it look at the sun, see how far away it is, and decide to calculate on its internal adding machine the inverse of the square of the distance, which tells it how much to move? This is certainly no explanation of the machinery of gravitation! You might want to look further, and various people have tried to look further. Newton was originally asked about his theory - 'But it doesn't mean anything - it doesn't tell us anything'. He said, 'It tells you how it moves. That should be enough. I have told you how it moves, not why.' But people often are unsatisfied without a mechanism, and I would like to describe one theory which has been invented, among others, of the type you might want. This theory suggests that this effect is the result of large numbers of actions, which would explain why it is mathematical.

Suppose that in the world everywhere there are a lot of particles, flying through us at very high speed. They come equally in all directions - just shooting by - and once in a while they hit us in a bombardment. We, and the sun, are practically transparent for them, practically but not completely, and some of them hit. Look, then, at what would happen(figure 1):

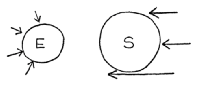
Figure 1

S is the sun, and E the earth. If the sun were not there, particles would be bombarding the earth from all sides, giving little impulses by the rattle, bang, bang of the few that hit. This will not shake the earth in any particular direction, because there are as many coming from one side as from the other, from top as from bottom. However, when the sun is there the particles which are coming from that direction are partly absorbed by the sun, because some of them hit the sun and do not go through. Therefore the number coming from the sun's direction towards the earth is less than the number coming from the other sides, because they meet an obstacle, the sun. It is easy to see that the farther the sun is away, of all the possible directions in which particles can come, a smaller proportion of the particles are being taken out. The sun will appear smaller - in fact inversely as the square of the distance. Therefore there will be an impulse on the earth towards the sun that varies inversely as the square of the distance. And this will be a result of large numbers of very simple operations, just hits, one after the other, from all directions. Therefore the strangeness of the mathematical relation will be very much reduced, because the fundamental operation is much simpler than calculating the inverse of the square of the distance. This design, with the particles bouncing, does the calculation.

   The only trouble with this scheme is that it does not work, for other reasons. Every theory that you make up has to be analysed against all possible consequences, to see if it predicts anything else. And this does predict something else. If the earth is moving, more particles will hit it from in front than from behind. (If you are running in the rain, more rain hits you in the front of the face than in the back of the head, because you are running into the rain.) So, if the earth is moving it is running into the particles coming towards it and away from the ones that are chasing it from behind. So more particles will hit it from the front than from the back, and there will be a force opposing any motion. This force would slow the earth up in its orbit, and it certainly would not have lasted the three or four billion years (at least) that it has been going around the sun. So that is the end of that theory. 'Well,' you say, 'it was a good one, and I got rid of the mathematics for a while. Maybe I could invent a better one.' Maybe you can, because nobody knows the ultimate. But up to today, from the time of Newton, no one has invented another theoretical description of the mathematical machinery behind this law which does not either say the same thing over again, or make the mathematics harder, or predict some wrong phenomena. So there is no model of the theory of gravitation today, other than the mathematical form.

If this were the only law of this character it would be interesting and rather annoying. But what turns out to be true is that the more we investigate, the more laws we find, and the deeper we penetrate nature, the more this disease persists. Every one of our laws is a purely mathematical statement in rather complex and abstruse mathematics. Newton's statement of the law of gravitation is relatively simple mathematics. It gets more and more abstruse and more and more difficult as we go on. Why? I have not the slightest idea. It is only my purpose here to tell you about this fact. The burden of the lecture is just to emphasize he fact that it is impossible to explain honestly the beauties of the laws of nature in a way that people can feel, without of their having some deep understanding of mathematics. I am sorry, but this seems to be the case. You might say, 'All right, then if there is no explanation the of law, at least tell me what the law is. Why not tell me in words instead of in symbols? Mathematics is just a language, and I want to be able to translate the language'. In fact I can, with patience, and I think I partly did. I could go a little further and explain in more detail that the equation means that if the distance is twice as far the force is one fourth as much, and so on. I could convert all the symbols into words. In other words I could be kind to the laymen as they all sit hopefully waiting for me to explain something. Different people get different reputations for their skill at explaining to the layman in layman's language these difficult and abstruse subjects. The layman then searches for book after book in the hope that he will avoid the complexities which ultimately set in, even with the best expositor of this type. He finds as he reads a generally increasing confusion, one complicated statement after another, one difficult-to-understand thing after another, all apparently disconnected from one another. It becomes obscure, and he hopes that maybe in some other book there is some explanation.... The author almost made it - maybe another fellow will make it right.

But I do not think it is possible, because mathematics is not just another language. Mathematics is a language plus reasoning; it is like a language plus logic. Mathematics is a tool for reasoning. It is in fact a big collection of the results of some person's careful thought and reasoning. By mathematics it is possible to connect one statement to another. For instance, I can say that the force is directed towards the sun. I can also tell you, as I did, that the planet moves so that if I draw a line from the sun to the planet, and draw another line at some definite period, like three weeks, later, then the area that is swung out by the planet is exactly the same as it will be in the next three weeks, and the next three weeks, and so on as it goes around the sun. I can explain both of those statements carefully, but I cannot explain why they are both the same. The apparent enormous complexities of nature, with all its funny laws and rules, each of which has been carefully explained to you, are really very closely interwoven. However, if you do not appreciate the mathematics, you cannot see, among the great variety of facts, that logic permits you to go from one to the other.

It may be unbelievable that I can demonstrate that equal areas will be swept out in equal times if the forces are directed towards the sun. So if I may, I will do one demonstration to show you that those two things really are equivalent, so that you can appreciate more than the mere statement of the two laws. I will show that the two laws are connected so that reasoning alone will bring you from one to the other, and that mathematics is just organized reasoning. Then you will appreciate the beauty of the relationship of the statements. I am going to prove the relationship that if the forces are directed towards the sun equal areas are swept out in equal times.

Figure 2

We start with a sun and a planet (fig. 2), and we imagine that at a certain time the planet is at position 1. It is moving in such a way that, say, one second later it has moved to position 2. If the sun did not exert a force on the planet, then, by Galileo's principle of inertia, it would keep right on going in a straight line. So after the same interval of time, the next second, it would have moved exactly the same distance in the same straight line, to the position 3. First we are going to show that if there is no force, then equal areas are swept out in equal times. I remind you that the area of a triangle is half the base times the altitude, and that the altitude is the vertical distance to the base. If the triangle is obtuse (fig. 3), then the altitude is the vertical height AD and the base is BC. Now let us compare the areas which would be swept out if the sun exerted no force whatsoever (fig- 2).

Figure 3

The two distances 1-2 and 2-3 are equal, remember. The question is, are the two areas equal ? Consider the triangle made from the sun and the two points 1 and 2. What is its area? It is the base 1-2, multiplied by half the perpendicular height from the baseline to S. What about the other triangle, the triangle in the motion from 2 to 3 ? Its area is the base 2-3, times half the perpendicular height to S. The two triangles have the same altitude, and, as I indicated, the same base, and therefore they have the same area. So far so good. If there were no force from the sun, equal areas would be swept out in equal times. But there is a force from the sun. During the interval 1-2-3 the sun is pulling and changing the motion in various directions towards itself. To get a good approximation we will take the central position, or average position, at 2, and say that the whole effect during the interval 1-3 was to change the motion by some amount in the direction of the line 2-S (fig. 4).

Figure 4

   This means that though the particles were moving on the line 1-2, and would, were there no force, have continued to move on the same line in the next second, because of the influence of the sun the motion is altered by an amount that is poking in a direction parallel to the line 2-S. The next motion is therefore a compound of what the planet wanted to do and the change that has been induced by the action of the sun. So the planet does not really end up at position 3, but rather at position 4. Now we would like to compare the areas of the triangles 23S and 24S, and I will show you that those are equal. They have the same base, S-2. Do they have the same altitude? Sure, because they are included between parallel lines. The distance from 4 to the line S-2 is equal to the distance from 3 to line S-2 (extended). Thus the area of the triangle S24 is the same as S23. I proved earlier that S12 and S23 were equal in area, so we now know S12 = S24. So, in the actual orbital motion of the planet the areas swept out in the first second and the second second are equal. Therefore, by reasoning, we can see a connection between the fact that the force is towards the sun, and the fact that the areas are equal. Isn't that ingenious ? I borrowed it straight from Newton. It comes right out of the Principia, diagram and all. Only the letters are different, because he wrote in Latin and these are Arabic numerals.

   Newton made all the proofs in his book geometrical. Today we do not use that kind of reasoning. We use a kind of analytic reasoning with symbols. It requires ingenuity to draw the correct triangles, to notice about the areas, and to figure out how to do this. But there have been improvements in the methods of analysis, which are faster and more efficient. I want to show what this looks like in the notation of the more modern mathematics, where you do nothing but write a lot of symbols to figure it out.

We want to talk about how fast the area changes, and we represent that by Ȧ. The area changes when the radius is swinging, and it is the component of velocity at right angles to the radius, times the radius, that tells us how fast the area changes. So this is the component of the radial distance multiplied by the velocity, or rate of change of the distance.

The question now is whether the rate of change of area itself changes. The principle is that the rate of change of the area is not supposed to change. So we differentiate this again, and this means some little trick about putting dots in the right place, that is all. You have to learn the tricks; it is just a series of rules that people have found out that are very useful for such a thing. We write:

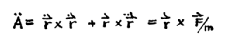
This first term says to take the component of the velocity at right angles to the velocity. It is zero; the velocity is in the same direction as itself. The acceleration, which is the second derivative, r with two dots, or the derivative of the velocity, is the force divided by the mass.

This says therefore that the rate of change of the rate of change of the area is the component of force at right angles to the radius, but if the force is in the direction of the radius,

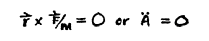
as Newton said, then there is no force at right angles to the radius, and that means that the rate of change of area does not change. This merely illustrates the power of analysis with different kinds of notation. Newton knew how to do this, more or less, with slightly different notations; but he wrote everything in the geometrical form, because he tried to make it possible for people to read his papers. He invented the calculus, which is the kind of mathematics Ihave just shown.

This is a good illustration of the relation of mathematics to physics. When the problems in physics become difficult we may often look to the mathematicians, who may already have studied such things and have prepared a line of  reasoning for us to follow. On the other hand they may not have, in which case we have to invent our own line of reasoning, which we then pass back to the mathematicians. Everybody who reasons carefully about anything is making a contribution to the knowledge of what happens when you think about something, and if you abstract it away and send it to the Department of Mathematics they put it in books as a branch of mathematics. Mathematics, then, is a way of going from one set of statements to another. It is evidently useful in physics, because we have these different ways in which we can speak of things, and mathematics permits us to develop consequences, to analyse the situations, and to change the laws in different ways to connect the various statements. In fact the total amount that a physicist knows is very little. He has only to remember the rules to get him from one place to another and he is all right, because all the various statements about equal times, the force being in the direction of the radius, and so on, are all interconnected by reasoning.

Now an interesting question comes up. Is there a place to begin to deduce the whole works ? Is there some particular pattern or order in nature by which we can understand that one set of statements is more fundamental and one set of statements more consequential ? There are two kinds of ways of looking at mathematics, which for the purpose of this lecture I will call the Babylonian tradition and the Greek tradition. In Babylonian schools in mathematics the student would learn something by doing a large number of examples until he caught on to the general rule. Also he would know a large amount of geometry, a lot of the properties of circles, the theorem of Pythagoras, formulae for the areas of cubes and triangles; in addition, some degree of argument was available to go from one thing to another. Tables of numerical quantities were available so that they could solve elaborate equations. Everything was prepared for calculating things out. But Euclid discovered that there was a way in which all of the theorems of geometry could be ordered from a set of axioms that were particularly simple. The Babylonian attitude - or what I call Babylonian  mathematics - is that you know all of the various theorems and many of the connections in between, but you have never fully realized that it could all come up from a bunch of axioms. The most modern mathematics concentrates on axioms and demonstrations within a very definite framework of conventions of what is acceptable and what is not acceptable as axioms. Modern geometry takes something like Euclid's axioms, modified to be more perfect, and then shows the deduction of the system. For instance, it would not be expected that a theorem like Pythagoras's (that the sum of the areas of squares put on two sides of a right- angled triangle is equal to the area of the square on the hypotenuse) should be an axiom. On the other hand, from another point of view of geometry, that of Descartes, the Pythagorean theorem is an axiom.

So the first thing we have to accept is that even in  mathematics you can start in different places. If all these various theorems are interconnected by reasoning there is no real way to say 'These are the most fundamental axioms', because if you were told something different instead you could also run the reasoning the other way. It is like a bridge with lots of members, and it is over-connected; if pieces have dropped out you can reconnect it another way. The mathematical tradition of today is to start with some particular ideas which are chosen by some kind of convention to be axioms, and then to build up the structure from there. What I have called the Babylonian idea is to say, 'I happen to know this, and I happen to know that, and maybe I know that; and I work everything out from there. Tomorrow I may forget that this is true, but remember that something else is true, so I can reconstruct it all again. I am never quite sure of where I am supposed to begin or where I am supposed to end. I just remember enough all the time so that as the memory fades and some of the pieces fall out I can put the thing back together again every day'. The method of always starting from the axioms is not very efficient in obtaining theorems. In working something out in geometry you are not very efficient if each time you have to start back at the axioms. If you have to remember a few things in geometry you can always get somewhere else, but it is much more efficient to do it the other way. To decide which are the best axioms is not necessarily the most efficient way of getting around in the territory. In physics we need the Babylonian method, and not the Euclidian or Greek method. I would like to explain why.

The problem in the Euclidian method is to make something about the axioms a little more interesting or important. But in the case of gravitation, for example, the question we are asking is: is it more important, more basic, or is it a better axiom, to say that the force is towards the sun, or to say that equal areas are swept out in equal times ? From one point of view the force statement is better. If I state what the forces are I can deal with a system with many particles in which the orbits are no longer ellipses, because the force statement tells me about the pull of one on the other. In this case the theorem about equal areas fails. Therefore I think that the force law ought to be an axiom instead of the other. On the other hand, the principle of equal areas can be generalized, in a system of a large number of particles, to another theorem. It is rather complicated to say, and not quite as pretty as the original statement about equal areas, but it is obviously its offspring. Take a system with a large number of particles, perhaps Jupiter, Saturn, the Sun, and lots of stars, all interacting with each other, and look at it from far away projected on a plane (fig. 5). The particles are all moving in various directions, and we take any point and calculate how much area is being swept out by the radius from this point to each of the particles. In this calculation the masses which are heavier count more strongly; if one particle is twice as heavy as another its area will count twice as much. So we count each of the areas swept out in proportion to the mass that is doing the sweeping, add them all together, and the resulting total is not changing in time. That total is called the angular momentum, and this is called the law of conservation of angular momentum. Conservation just means that it does not change.

Figure 5

One of the consequences of this is as follows. Imagine a lot of stars falling together to form a nebula, or galaxy. At first they are very far out, on long radii from the centre, moving slowly and allowing a small amount of area to be generated. As they come closer the distances to the centre will shorten, and when they are very far in the radii will be very small, so in order to produce the same area per second they will have to move a great deal faster. You will see then that as the stars come in they will swing and swirl around faster and faster, and thus we can roughly understand the qualitative shape of the spiral nebulae. In the same way we can understand how a skater spins. He starts with his leg out, moving slowly, and as he pulls his leg in he spins faster. When the leg is out it is contributing a certain amount of area per second, and then when he brings his leg in he has to spin much faster to produce the same amount of area. But I did not prove it for the skater: the skater uses muscle force, and gravity is a different force. Yet it is true for the skater.

Now we have a problem. We can deduce often from one part of physics, like the Law of Gravitation, a principle which turns out to be much more valid than the derivation. This does not happen in mathematics; theorems do not come out in places where they are not supposed to be. In other words, if we were to say that the postulate of physics was the equal area law of gravitation, then we could deduce the conservation of angular momentum, but only for  gravitation. Yet we discover experimentally that the conservation of angular momentum is a much wider thing. Newton had other postulates by which he could get the more general conservation law of angular momentum. But these Newtonian laws were wrong. There are no forces, it is all a lot of boloney, the particles do not have orbits, and so on. Yet the analogue, the exact transformation of this principle about the areas and the conservation of angular momentum, is true. It works for atomic motions in quantum mechanics, and, as far as we can tell, it is still exact today. We have these wide principles which sweep across the different laws, and if we take the derivation too seriously, and feel that one is only valid because another is valid, then we cannot understand the interconnections of the different branches of physics. Someday, when physics is complete and we know all the laws, we may be able to start with some axioms, and no doubt somebody will figure out a particular way of doing it so that everything else can be deduced. But while we do not know all the laws, we can use some to make guesses at theorems which extend beyond the proof. In order to  understand physics one must always have a neat balance, and contain in one's head all of the various propositions and their interrelationships, because the laws often extend beyond the range of their deductions. This will only have no importance when all the laws are known.

Another thing, a very strange one, that is interesting in the relation of mathematics to physics is the fact that by mathematical arguments you can show that it is possible to start from many apparently different starting points, and yet come to the same thing. That is pretty clear. If you have axioms, you can instead use some of the theorems; but actually the physical laws are so delicately constructed that the different but equivalent statements of them have such qualitatively different characters, and this makes them very interesting. To illustrate this I am going to state the law of gravitation in three different ways, all of which are exactly equivalent but sound completely different.

The first statement is that there are forces between objects, according to the equation which I have given you before.

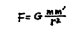
Each object, when it sees the force on it, accelerates or changes its motion, at a certain amount per second. It is the regular way of stating the law, I call it Newton's law. This statement of the law says that the force depends on something at a finite distance away. It has what we call an unlocal quality. The force on one object depends on where another one is some distance away.

You may not like the idea of action at a distance. How can this object know what is going on over there? So there is another way of stating the laws, which is very strange, called the field way. It is hard to explain, but I want to give you some rough idea of what it is like. It says a completely different thing. There is a number at every point in space (I know it is a number, not a mechanism: that is the trouble with physics, it must be mathematical), and the numbers change when you go from place to place. If an object is placed at a point in space, the force on it is in the direction in which that number changes most rapidly (I will give it its usual name, the potential, the force is in the direction in which the potential changes). Further, the force is proportional to how fast the potential changes as you move. That is one part of the statement, but it is not enough, because I have yet to tell you how to determine the way in which the potential varies. I could say the potential varies inversely as the distance from each object, but that is back to the reaction-at-a-distance idea. You can state the law in another way, which says that you do not have to know what is going on anywhere outside a little ball. If you want to know what the potential is at the centre of the ball, you need only tell me what it is on the surface of the ball, however small. You do not have to look outside, you just tell me what it is in the neighbourhood, and how much mass there is in the ball. The rule is this. The potential at the centre is equal to the average of the potential on the surface of the ball, minus the same constant, G, as we had in the other equation, divided by twice the radius of the ball (which we will call a), and then multiplied by the mass inside the ball, if the ball is small enough.

You see that this law is different from the other, because it tells what happens at one point in terms of what happens very close by. Newton's law tells what happens at one time in terms of what happens at another instant. It gives from instant to instant how to work it out, but in space leaps from place to place. The second statement is both local in time and local in space, because it depends only on what is in the neighbourhood. But both statements are exactly equivalent mathematically.

There is another completely different way of stating this, different in the philosophy and the qualitative ideas involved. If you do not like action at a distance I have shown you can get away without it. Now I want to show you a statement which is philosophically the exact opposite. In this there is no discussion at all about how the thing works its way from place to place; the whole is contained in an overall statement, as follows. When you have a number of particles, and you want to know how one moves from one place to another, you do it by inventing a possible motion

that gets from one place to the other in a given amount of time (fig. 6). Say the particle wants to go from X to Y in an hour, and you want to know by what route it can go. What you do is to invent various curves, and calculate on each curve a certain quantity. (I do not want to tell you what the quantity is, but for those who have heard of these terms the quantity on each route is the average of the difference between the kinetic and the potential energy.) If you calculate this quantity for one route, and then for another, you will get a different number for each route. There is one route which gives the least possible number, however, and that is the route that the particle in nature actually takes! We are now describing the actual motion, the ellipse, by saying something about the whole curve. We have lost the idea of causality, that the particle feels the pull and moves in accordance with it. Instead of that, in some grand fashion it smells all the curves, all the possibilities, and decides which one to take (by choosing that for which our quantity is least).

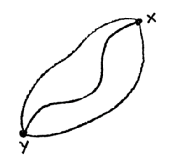
Figure 6

This is an example of the wide range of beautiful ways of describing nature. When people say that nature must have causality, you can use Newton's law; or if they say that nature must be stated in terms of a minimum principle, you talk about it this last way; or if they insist that nature must have a local field - sure, you can do that. The question is: which one is right? If these various alternatives are not exactly equivalent mathematically, if for certain ones there will be different consequences than for others, then all we have to do is to experiment to find out which way nature actually chooses to do it. People may come along and argue philosophically that they like one better than another; but we have learned from much experience that all philosophical intuitions about what nature is going to do fail. One just has to work out all the possibilities, and try all the  alternatives. But in the particular case I am talking about the theories are exactly equivalent. Mathematically each of the three different formulations, Newton's law, the local field method and the minimum principle, gives exactly the same consequences. What do we do then? You will read in all the books that we cannot decide scientifically on one or the other. That is true. They are equivalent scientifically. It is impossible to make a decision, because there is no experimental way to distinguish between them if all the consequences are the same. But psychologically they are very different in two ways. First, philosophically you like them or do not like them; and training is the only way to beat that disease. Second, psychologically they are different because they are completely unequivalent when you are trying to guess new laws.

As long as physics is incomplete, and we are trying to understand the other laws, then the different possible formulations may give clues about what might happen in other circumstances. In that case they are no longer equivalent, psychologically, in suggesting to us guesses about what the laws may look like in a wider situation. To give an example, Einstein realized that electrical signals could not propagate faster than the speed of light. He guessed that it was a general principle. (This is the same guessing game as taking the angular momentum and extending it from one case where you have proved it, to the rest of the phenomena of the universe.) He guessed that it was true of everything, and he guessed that it would be true of gravitation. If signals  cannot go any faster than the speed of light, then it turns out that the method of describing the forces instantaneously is very poor. So in Einstein's generalization of gravitation Newton's method of describing physics is hopelessly inadequate and enormously complicated, whereas the field method is neat and simple, and so is the minimum principle. We have not decided between the last two yet.

In fact it turns out that in quantum mechanics neither is right in exactly the way I have stated them, but the fact that a minimum principle exists turns out to be a consequence of the fact that on a small scale particles obey quantum mechanics. The best law, as at present understood, is really a combination of the two in which we use minimum principles plus local laws. At present we believe that the laws of physics have to have the local character and also the minimum principle, but we do not really know. If you have a structure that is only partly accurate, and something is going to fail, then if you write it with just the right axioms maybe only one axiom fails and the rest remain, you need only change one little thing. But if you write it with another set of axioms they may all collapse, because they all lean on that one thing that fails. We cannot tell ahead of time, without some intuition, which is the best way to write it so that we can find out the new situation. We must always keep ll the alternative ways of looking at a thing in our heads; so physicists do Babylonian mathematics, and pay but little attention to the precise reasoning from fixed axioms.

One of the amazing characteristics of nature is the variety of interpretational schemes which is possible. It turns out that it is only possible because the laws are just so, special and delicate. For instance, that the law is the inverse square is what permits it to become local; if it were the inverse cube it could not be done that way. At the other end of the equation, the fact that the force is related to the rate of change of velocity is what permits the minimum principle way of writing the laws. If, for instance, the force were proportional to the rate of change of position instead of velocity, then you could not write it in that way. If you modify the laws much you find that you can only write them in fewer ways. I always find that mysterious, and I do not understand the reason why it is that the correct laws of physics seem to be expressible in such a tremendous variety of ways. They seem to be able to get through several wickets at the same time.

I should like to say a few things on the relation of mathematics and physics which are a little more general.  Mathematicians are only dealing with the structure of reasoning, and they do not really care what they are talking about. They do not even need to know what they are talking about, or, as they themselves say, whether what they say is true. I will explain that. You state the axioms, such-and-such is so, and such-and-such is so. What then? The logic can be carried out without knowing what the such-and-such words mean. If the statements about the axioms are carefully formulated and complete enough, it is not necessary for the man who is doing the reasoning to have any knowledge of the meaning of the words in order to deduce new  conclusions in the same language. If I use the word triangle in one of the axioms there will be a statement about triangles in the conclusion, whereas the man who is doing the reasoning may not know what a triangle is. But I can read his  reasoning back and say, Triangle, that is just a three-sided what- have-you, which is so-and-so', and then I know his new facts. In other words, mathematicians prepare abstract reasoning ready to be used if you have a set of axioms about the real world. But the physicist has meaning to all his phrases. That is a very important thing that a lot of people who come to physics by way of mathematics do not appreciate. Physics is not mathematics, and mathematics is not physics. One helps the other. But in physics you have to have an  understanding of the connection of words with the real world. It is necessary at the end to translate what you have figured out into English, into the world, into the blocks of copper and glass that you are going to do the experiments with. Only in that way can you find out whether the consequences are true. This is a problem which is not a problem of mathematics at all.

Of course it is obvious that the mathematical reasonings which have been developed are of great power and use for physicists. On the other hand, sometimes the physicists' reasoning is useful for mathematicians.

Mathematicians like to make their reasoning as general as possible. If I say to them, 'I want to talk about ordinary three dimensional space', they say 'If you have a space of n dimensions, then here are the theorems'. 'But I only want the case 3', 'Well, substitute n = 3.'! So it turns out that many of the complicated theorems they have are much simpler when adapted to a special case. The physicist is always interested in the special case; he is never interested in the general case. He is talking about something; he is not talking abstractly about anything. He wants to discuss the gravity law in three dimensions; he never wants the arbitrary force case in n dimensions. So a certain amount of reducing is necessary, because the mathematicians have prepared these things for a wide range of problems. This is very useful, and later on it always turns out that the poor physicist has to come back and say, 'Excuse me, when you wanted to tell me about four dimensions ...'

When you know what it is you are talking about, that some symbols represent forces, others masses, inertia, and so on, then you can use a lot of commonsense, seat-of-the-pants feeling about the world. You have seen various things, and you know more or less how the phenomenon is going to behave. But the poor mathematician translates it into equations, and as the symbols do not mean anything to him he has no guide but precise mathematical rigour and care in the argument. The physicist, who knows more or less how the answer is going to come out, can sort of guess part way, and so go along rather rapidly. The mathematical rigour of great precision is not very useful in physics. But one should not criticize the mathematicians on this score. It is not necessary that just because something would be useful to physics they have to do it that way. They are doing their own job. If you want something else, then you work it out for yourself.

The next question is whether, when trying to guess a new law, we should use the seat-of-the-pants feeling and  philosophical principles – ‘I don't like the minimum principle', or‘I do like the minimum principle', 'I don't like action at a distance', or ‘I do like action at a distance'. To what extent do models help? It is interesting that very often models do help, and most physics teachers try to teach how to use models and to get a good physical feel for how things are going to work out. But it always turns out that the greatest discoveries abstract away from the model and the model never does any good. Maxwell's discovery of electrodynamics was first made with a lot of imaginary wheels and idlers in space. But when you get rid of all the idlers and things in space the thing is O.K. Dirac discovered the correct laws for relativity quantum mechanics simply by guessing the equation. The method of guessing the equation seems to be a pretty effective way of guessing new laws. This shows again that mathematics is a deep way of expressing nature, and any attempt to express nature in philosophical principles, or in seat-of-the-pants mechanical feelings, is not an efficient way.

It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time. How can all that be going on in that tiny space? Why should it take an infinite amount of logic to figure out what one tiny piece of space/time is going to do? So I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple, like the chequer board with all its apparent complexities. But this speculation is of the same nature as those other people make - 'I like it', 'I don't like it', - and it is not good to be too prejudiced about these things.

To summarize, I would use the words of Jeans, who said that 'the Great Architect seems to be a mathematician'. To those who do not know mathematics it is difficult to get across a real feeling as to the beauty, the deepest beauty, of nature. C. P. Snow talked about two cultures. I really think that those two cultures separate people who have and people who have not had this experience of understanding mathematics well enough to appreciate nature once.

It is too bad that it has to be mathematics, and that mathematics is hard for some people. It is reputed -1 do not know if it is true - that when one of the kings was trying to learn geometry from Euclid he complained that it was difficult. And Euclid said, There is no royal road to geometry'. And there is no royal road. Physicists cannot make a conversion to any other language. If you want to learn about nature, to appreciate nature, it is necessary to understand the language that she speaks in. She offers her information only in one form; we are not so unhumble as to demand that she change before we pay any attention.

All the intellectual arguments that you can make will not communicate to deaf ears what the experience of music really is. In the same way all the intellectual arguments in the world will not convey an understanding of nature to those of 'the other culture'. Philosophers may try to teach you by telling you qualitatively about nature. I am trying to describe her. But it is not getting across because it is impossible. Perhaps it is because their horizons are limited in this way that some people are able to imagine that the centre of the universe is man.