变形—位移
translate()函数可以将元素向指定的方向移动,类似于position中的relative。或以简单的理解为,使用translate()函数,可以把元素从原来的位置移动,而不影响在X、Y轴上任何web组件。
translate我们分为三种情况:
1. translate(X,Y)水平方向或垂直方向同时移动(也就是X轴和Y轴同时移动)
2. translateX(X)仅水平方向移动(X轴移动)
3. translateY(Y)仅垂直方向移动(Y轴移动)
用法:transform:translate(20x,40x);
效果:
变形—矩阵matrix()
matrix():是一个含六个值的(m11,m12, m21,m22,dx,dy)变换矩一个2D变换,相当于直接应用一个[m11,m12, m21,m22,dx,dy]变换矩阵。就是基于水平方向(X轴)和垂直方向(Y轴)重新定位元素,此属性值使用涉及到数学中的矩阵。
下列案例实现translate案例中的效果。
用法:transform:matrix(1,0,0,1,20,40);
效果:
变形—原点transform-origin
变形—原点 transform-origin:任何一个元素都有一个中心点,默认情况下,其中心点是居于元素X轴和Y轴的50%处。
在没有重置transform-origin改变元素原点位置的情况下,CSS变形进行的旋转、位移、缩放、扭曲等操作都是以元素自己中心位置进行变形。但是很多时候,我们可以通过transform-origin来对元素进行原点位置改变,使元素原点不在元素的中心位置,以达到需要的原点位置。
transform-origin取值和元素设置背景中的background-position取值类似,如下表所示:
关键字 百分数
top=top center 50% 0
left=left center 0 50%
bottom=bottom center 50% 100%
right=right center 100% 50%
center=center center 50% 50%
top left=right top 0 0
top right=right top 0 100%
bottom left=left bottom 100% 0
bottom right=right bottom 100% 100%
用法:transform-origin: left;
效果: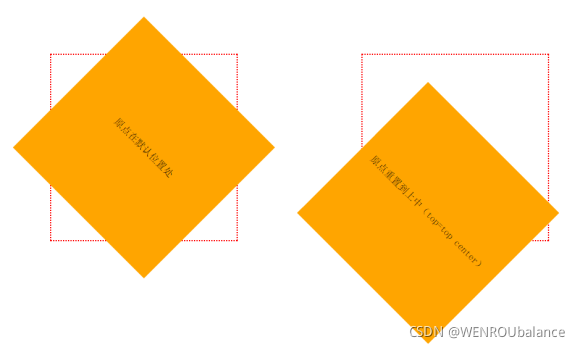








 本文介绍了CSS中的变形方法,包括translate的三种用法:translate(X,Y)、translateX(X)和translateY(Y),以及matrix的使用,它通过2D变换矩阵实现元素定位。此外,还讨论了transform-origin属性,用于改变元素变形的中心点,以实现更灵活的布局效果。"
80015812,2300319,Kafka新消费者详解与实战,"['Kafka', '消费者', '消息队列', '数据处理']
本文介绍了CSS中的变形方法,包括translate的三种用法:translate(X,Y)、translateX(X)和translateY(Y),以及matrix的使用,它通过2D变换矩阵实现元素定位。此外,还讨论了transform-origin属性,用于改变元素变形的中心点,以实现更灵活的布局效果。"
80015812,2300319,Kafka新消费者详解与实战,"['Kafka', '消费者', '消息队列', '数据处理']
















 5456
5456

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








