机器学习分类算法实践:逻辑回归模型分类预测

原创于 2025-10-30 17:29:10 发布 · 938 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #分类 #逻辑回归 #线性回归 #python

部署运行你感兴趣的模型镜像

使用 Kaggle Titanic 数据集的 Logistic 回归

学习目标

本课程基于Kaggle泰坦尼克号乘客数据集，通过构建逻辑回归模型，分析舱位等级、性别、年龄等关键变量对生存概率的影响，实现乘客生存情况的分类预测。

学习内容

1 逻辑回归模型分类预测

Logistic回归模型:

Logistic回归是一种用于解决分类问题的统计模型，尤其适合预测“是/否”“成功/失败”这类二分类结果。它的核心是计算某个事件发生的概率。

和线性回归的区别:
    线性回归：直接预测数值（比如房价、温度）。  
    Logistic回归：预测概率（比如“用户点击广告的概率”），并通过设定阈值（如0.5）转化为分类结果。

核心原理:
    将输入特征（如年龄、收入）通过一个S形曲线（Sigmoid函数）映射到0~1之间，表示概率。  
    模型通过调整参数，使得预测概率尽可能接近真实标签（比如真实点击=1，未点击=0）。

优点:
    输出可解释（直接是概率）。  
    计算高效，适合大规模数据。  
    可以扩展处理多分类问题（如Softmax回归）。

缺点:
    假设特征与结果间是线性关系（复杂关系需特征工程）。  
    对异常值和多重共线性敏感。

典型应用场景:  
    垃圾邮件检测（是/否垃圾）。  
    疾病预测（患病/健康）。  
    用户行为预测（购买/不购买）。

Logistic回归通过概率解决二分类问题，简单高效，但需注意数据本身的限制。

1.1 配置运行环境

加载数据集

!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_datasets/50286808e39c11ef9be6fa163edcddae/train.csv

安装seaborn库

%pip install seaborn

导入相关的库，读取数据

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

train = pd.read_csv('train.csv') # Training set is already available
train.head()

检查数据集的基本信息，重点关注其中是否存在缺失值。

t=train.info()
d=train.describe()
d

1.2 探索性分析和绘图

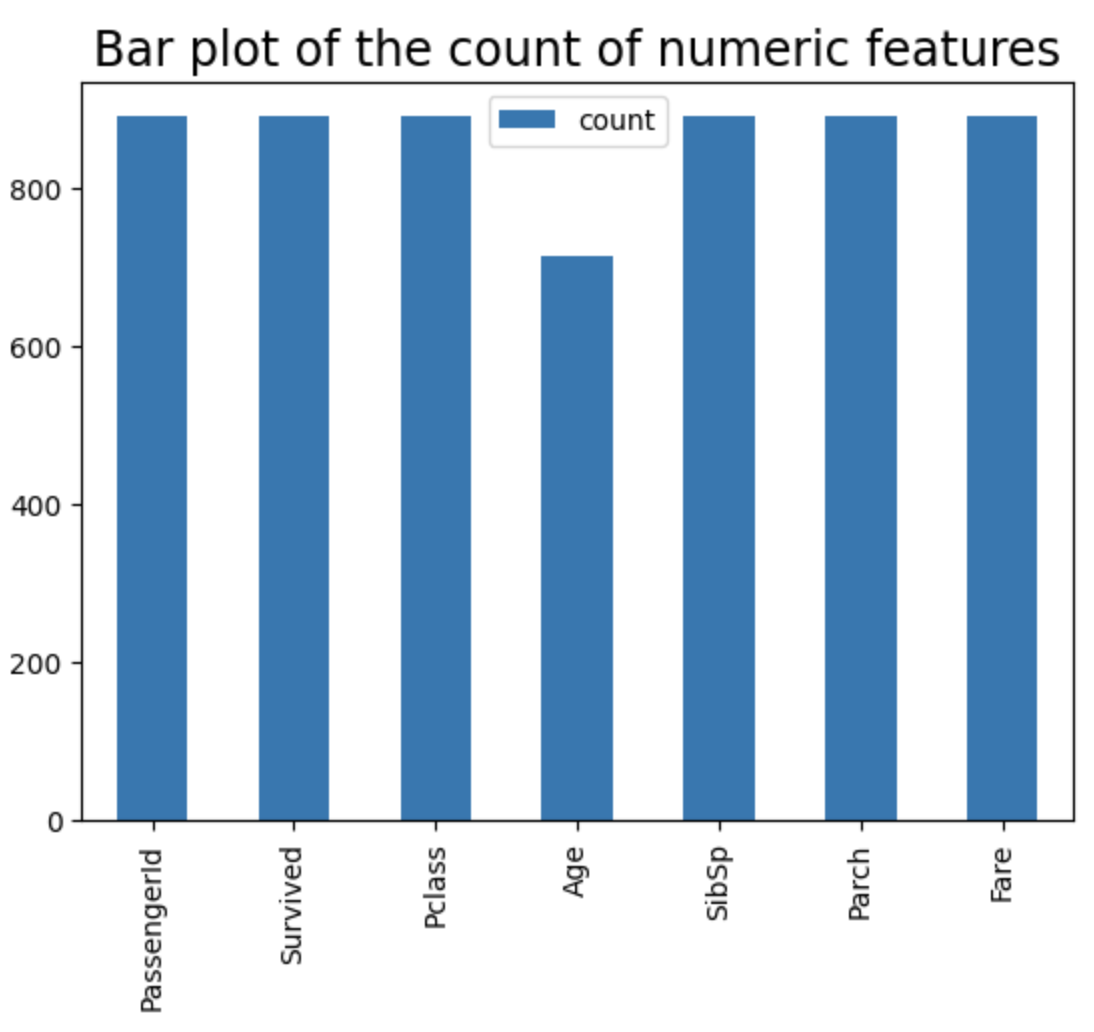
绘制条形图以检查数字条目的数量

从条形图可以看出，“Age”列的计数低于其他列的计数，这表明存在一些缺失的“Age”条目。为了处理这些缺失值，我们可以对数据进行插补或转换，以填补缺失的条目。

dT=d.T
dT.plot.bar(y='count')
plt.title("Bar plot of the count of numeric features",fontsize=17)

在这里插入图片描述
检查存活者与未存活者的相对比例

sns.set_style('whitegrid')
sns.countplot(x='Survived',data=train,palette='RdBu_r')

是否存在基于性别的生存模式

从数据来看，女性的存活率似乎高于男性！

sns.set_style('whitegrid')
sns.countplot(x='Survived',hue='Sex',data=train,palette='RdBu_r')

是否存在与乘客等级相关的模式

从数据中可以看出，三等舱的死亡人数显著高于其他舱位。

sns.set_style('whitegrid')
sns.countplot(x='Survived',hue='Pclass',data=train,palette='rainbow')

计算并绘制每个类别中幸存乘客的比例。

f_class_survived=train.groupby('Pclass')['Survived'].mean()
f_class_survived = pd.DataFrame(f_class_survived)
f_class_survived
f_class_survived.plot.bar(y='Survived')
plt.title("Fraction of passengers survived by class",fontsize=17)

是否存在与拥有兄弟姐妹或配偶相关的模式

从数据中可以看出，似乎存在一个微弱的趋势：拥有更多兄弟姐妹或配偶的乘客，其存活率略有提高。

sns.set_style('whitegrid')
sns.countplot(x='Survived',hue='SibSp',data=train,palette='rainbow')

整体年龄分布

plt.xlabel("Age of the passengers",fontsize=18)
plt.ylabel("Count",fontsize=18)
plt.title("Age histogram of the passengers",fontsize=22)
train['Age'].hist(bins=30,color='darkred',alpha=0.7,figsize=(10,6))

不同乘客等级的年龄分布情况

从数据来看，三个乘客等级的平均年龄存在差异，呈现从一等舱到三等舱逐渐降低的趋势。

plt.figure(figsize=(12, 10))
plt.xlabel("Passenger Class",fontsize=18)
plt.ylabel("Age",fontsize=18)
sns.boxplot(x='Pclass',y='Age',data=train,palette='winter')

f_class_Age=train.groupby('Pclass')['Age'].mean()
f_class_Age = pd.DataFrame(f_class_Age)
f_class_Age.plot.bar(y='Age')
plt.title("Average age of passengers by class",fontsize=17)
plt.ylabel("Age (years)", fontsize=17)
plt.xlabel("Passenger class", fontsize=17)

1.3 数据预处理

对年龄进行插补（采用平均值）。
删除不必要的特征。
将分类特征转换为虚拟变量。

插补年龄（通过平均值）

定义一个函数以填充“age”特征的缺失值。

a=list(f_class_Age['Age'])

def impute_age(cols):
    Age = cols[0]
    Pclass = cols[1]
    
    if pd.isnull(Age):

        if Pclass == 1:
            return a[0]

        elif Pclass == 2:
            return a[1]

        else:
            return a[2]

    else:
        return Age

绘制数值特征的计数条形图。

train['Age'] = train[['Age','Pclass']].apply(impute_age,axis=1)
d=train.describe()
dT=d.T
dT.plot.bar(y='count')
plt.title("Bar plot of the count of numeric features",fontsize=17)

删除不必要的特征

删除 ‘Cabin’ 特征以及任何其他包含空值的特征。

train.drop('Cabin',axis=1,inplace=True)
train.dropna(inplace=True)
train.head()

删除其他不必要的特征，例如“PassengerId”、“Name”和“Ticket”。

train.drop(['PassengerId','Name','Ticket'],axis=1,inplace=True)
train.head()

将分类特征转换为虚拟变量

将“Sex”和“Embarked”等分类特征转换为虚拟变量。

sex = pd.get_dummies(train['Sex'],drop_first=True)
embark = pd.get_dummies(train['Embarked'],drop_first=True)

删除“Sex”及“Embarked”特征，并将其对应的虚拟变量列进行合并。

train.drop(['Sex','Embarked'],axis=1,inplace=True)
train = pd.concat([train,sex,embark],axis=1)
train.head()

该数据集现已完成预处理，可用于逻辑回归分析。

1.4 Logistic 回归模型拟合与预测

首先，将数据集拆分为训练集和测试集。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(train.drop('Survived',axis=1), 
                                                    train['Survived'], test_size=0.30, 
                                                    random_state=111)

使用F1-score作为模型正则化的评估指标。

通过散点图展示了正则化参数（惩罚参数）与F1分数之间的关系。横轴是惩罚参数（正则化强度的倒数），纵轴是模型在测试数据上的F1分数。通过观察散点图，可以发现：

F1分数随着惩罚参数的变化而变化，从而确定最优的正则化参数范围。
如果F1分数在某个惩罚参数值附近达到最高点，说明该参数值附近是模型性能最佳的区域。
如果F1分数随着惩罚参数的增加持续下降，说明模型在较强的正则化下性能变差；反之，如果持续上升，说明模型在较弱的正则化下性能更好。

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report

# 初始化多个列表，用于存储不同正则化参数下的模型、预测结果、分类报告和 F1 分数。
nsimu=201
penalty=[0]*nsimu
logmodel=[0]*nsimu
predictions =[0]*nsimu
class_report = [0]*nsimu
f1=[0]*nsimu

# 通过循环，对不同的正则化参数 C 训练逻辑回归模型，计算预测结果和 F1 分数，并记录每个模型的惩罚参数。
for i in range(1,nsimu):
        logmodel[i] =(LogisticRegression(C=i/1000,tol=1e-4, max_iter=100,n_jobs=4))
        logmodel[i].fit(X_train,y_train)
        predictions[i] = logmodel[i].predict(X_test)
        class_report[i] = classification_report(y_test,predictions[i])
        l=class_report[i].split()
        f1[i] = l[len(l)-2]
        penalty[i]=1000/i

# 绘制惩罚参数与 F1 分数的散点图，展示正则化参数对模型性能的影响。
plt.scatter(penalty[1:len(penalty)-2],f1[1:len(f1)-2])
plt.title("F1-score vs. regularization parameter",fontsize=20)
plt.xlabel("Penalty parameter",fontsize=17)
plt.ylabel("F1-score on test data",fontsize=17)
plt.show()

测试集划分比例对F1分数的影响。

# 初始化变量，用于存储不同测试集大小下的分类报告、F1 分数和测试集占比。
nsimu=101
class_report = [0]*nsimu
f1=[0]*nsimu
test_fraction =[0]*nsimu

# 循环训练逻辑回归模型，每次使用不同的测试集大小（从 10% 逐渐增加），计算并记录每个模型的 F1 分数和测试集占比。
for i in range(1,nsimu):
        X_train, X_test, y_train, y_test = train_test_split(train.drop('Survived',axis=1), 
                                                    train['Survived'], test_size=0.1+(i-1)*0.007, 
                                                    random_state=111)
        logmodel =(LogisticRegression(C=1,tol=1e-4, max_iter=1000,n_jobs=4))
        logmodel.fit(X_train,y_train)
        predictions = logmodel.predict(X_test)
        class_report[i] = classification_report(y_test,predictions)
        l=class_report[i].split()
        f1[i] = l[len(l)-2]
        test_fraction[i]=0.1+(i-1)*0.007

# 绘制测试集占比与 F1 分数的折线图，展示测试集大小对模型性能的影响。
plt.plot(test_fraction[1:len(test_fraction)-2],f1[1:len(f1)-2])
plt.title("F1-score vs. test set size (fraction)",fontsize=20)
plt.xlabel("Test set size (fraction)",fontsize=17)
plt.ylabel("F1-score on test data",fontsize=17)
plt.show()

将F1分数定义为测试/训练数据集拆分随机种子的函数关系。

# 初始化变量，用于存储不同随机种子下的分类报告、F1 分数和随机种子值。
nsimu=101
class_report = [0]*nsimu
f1=[0]*nsimu
random_init =[0]*nsimu

# 循环训练逻辑回归模型，每次使用不同的随机种子（从 101 到 200）进行数据划分，计算并记录每个模型的 F1 分数和对应的随机种子值。
for i in range(1,nsimu):
        X_train, X_test, y_train, y_test = train_test_split(train.drop('Survived',axis=1), 
                                                    train['Survived'], test_size=0.3, 
                                                    random_state=i+100)
        logmodel =(LogisticRegression(C=1,tol=1e-5, max_iter=1000,n_jobs=4))
        logmodel.fit(X_train,y_train)
        predictions = logmodel.predict(X_test)
        class_report[i] = classification_report(y_test,predictions)
        l=class_report[i].split()
        f1[i] = l[len(l)-2]
        random_init[i]=i+100

# 绘制随机种子与 F1 分数的折线图，展示随机种子对模型性能的影响。
plt.plot(random_init[1:len(random_init)-2],f1[1:len(f1)-2])
plt.title("F1-score vs. random initialization seed",fontsize=20)
plt.xlabel("Random initialization seed",fontsize=17)
plt.ylabel("F1-score on test data",fontsize=17)
plt.show()