分类与预测—回归分析
一、回归分析
- 回归分析:是一种通过建立模型来研究变量之间相互关系的一切关系、结构状态及进行模型预测的有效工具。
- 常见的回归方法:线性回归、非线性回归、逻辑斯蒂回归、岭回归、主成分回归。
- 回归分析通常所预测的目标函数是连续值。
线性回归
例:一元线性回归:某产品电视广告投入x(以百万元为单位)与产品销售量y(以亿个为单位)的数据。
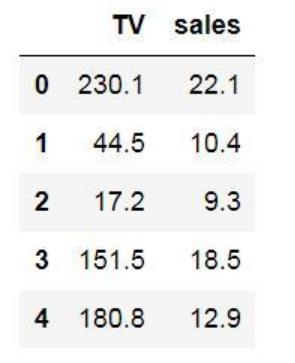
Y = 0.049693x + 6.7784
x=100,y=1174.8
给定由m个属性描述的样本x=(x1;x2;…;xm),其中xi是x在第i个属性上的取值,线性回归(linear regression)试图学得一个通过属性值的线性组合来进行预测的函数∶
f
(
x
)
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
m
x
m
+
b
f(x)=w_1x_1+w_2x_2+...+w_mx_m+b
f(x)=w1x1+w2x2+...+wmxm+b
一般用向量的形式写成∶
f
(
x
)
=
w
T
+
b
f(x)=w^T+b
f(x)=wT+b
其中w=(w1;w2;…;wm)。
给定训练数D={(x1,y1),(x2,y2),…,(xi,yi),…,(xn,yn)}其中xi=(xi1;xi2;…;xim),yi∈R
可用最小二乘法(least square method)对w 和b进行估计。
下面以一元线性回归为例,来详细讲解w和b的最小二乘法估计
f
(
x
i
)
=
w
x
i
+
b
,使得
f
(
x
i
)
≃
y
i
f(x_i)=wx_i+b,使得f(x_i)\simeq y_i
f(xi)=wxi+b,使得f(xi)≃yi
最小二乘法就是基于预测值和真实值的均方差最小化的方法来估计参数w和b∶
(
w
∗
,
b
∗
)
=
arg
min
(
w
,
b
)
∑
i
=
1
n
(
f
(
x
i
)
−
y
i
)
2
=
arg
min
(
w
,
b
)
∑
i
=
1
n
(
y
i
−
w
x
i
−
b
)
2
\begin{aligned} \left(w^*, b^*\right) &=\underset{(w, b)}{\arg \min } \sum_{i=1}^n\left(f\left(x_i\right)-y_i\right)^2 \\ &=\underset{(w, b)}{\arg \min } \sum_{i=1}^n\left(y_i-w x_i-b\right)^2 \end{aligned}
(w∗,b∗)=(w,b)argmini=1∑n(f(xi)−yi)2=(w,b)argmini=1∑n(yi−wxi−b)2
最小化均方误差
E
(
w
,
b
)
=
∑
i
=
1
n
(
y
i
−
w
x
i
−
b
)
2
E_{(w,b)}=\sum^n_{i=1}(y_i-wx_i-b)^2
E(w,b)=i=1∑n(yi−wxi−b)2
分别对
w
w
w和
b
b
b求偏导,可得
∂
E
(
w
,
b
)
∂
w
=
2
(
w
∑
i
=
1
n
x
i
2
−
∑
i
=
1
n
(
y
i
−
b
)
x
i
)
∂
E
(
w
,
b
)
∂
b
=
2
(
n
b
−
∑
i
=
1
n
(
y
i
−
w
x
i
)
)
\frac{\partial E_{(w,b)}}{\partial w}=2(w\sum^n_{i=1}x_i^2-\sum^n_{i=1}(y_i-b)x_i)\\ \frac{\partial E_{(w,b)}}{\partial b}=2(nb-\sum^n_{i=1}(y_i-wx_i))
∂w∂E(w,b)=2(wi=1∑nxi2−i=1∑n(yi−b)xi)∂b∂E(w,b)=2(nb−i=1∑n(yi−wxi))
令上两式为零可得到
w
w
w和
b
b
b 最优解的闭式(closed-form)解:
w
=
∑
i
=
1
n
y
i
(
x
i
−
x
ˉ
)
∑
i
=
1
n
x
i
2
−
1
n
(
∑
i
=
1
n
x
i
)
2
b
=
1
n
∑
i
=
1
n
(
y
i
−
w
x
i
)
w=\frac{\sum^n_{i=1}y_i(x_i-\bar{x})}{\sum^n_{i=1}x_i^2-\frac{1}{n}(\sum^n_{i=1}x_i)^2} \\b=\frac{1}{n}\sum^n_{i=1}(y_i-wx_i)
w=∑i=1nxi2−n1(∑i=1nxi)2∑i=1nyi(xi−xˉ)b=n1i=1∑n(yi−wxi)
其中,
x
ˉ
=
1
n
∑
i
=
1
n
x
i
\bar{x}=\frac{1}{n}\sum^n_{i=1}x_i
xˉ=n1∑i=1nxi
只要学到w和b,模型就可以确定;对于任意的测试样例 x x x,只要输入它的属性值,就可以输出它的预测值。
线性回归假定输入空间到输出空间的函数映射成线性关系,但现实应用中,很多问题都是非线性的。为拓展其应用场景,我们可以将线性回归的预测值做一个非线性的函数变化去逼近真实值,这样得到的模型统称为广义线性回归(generalized linear regression):
y
=
g
(
w
T
x
+
b
)
y=g(w^Tx+b)
y=g(wTx+b)
其中g(·)称为联系函数(link function)。
理论上,联系函数g(·)可以是任意函数,比如当g(·)被指定为指数函数时,得到的回归模型称为对数线性回归
y
=
e
w
T
x
+
b
y=e^{w^Tx+b}
y=ewTx+b
之所以叫对数线性回归,是因为它将真实值的对数作为线性回归逼近的目标,即∶
l
n
y
=
w
T
x
+
b
lny=w^Tx+b
lny=wTx+b
逻辑斯蒂回归
前面的内容都是在讲解如何利用线性模型进行回归学习,完成回归任务。但如果我们要做的是分类任务该怎么办?
为了简化,我们先考虑二分类任务,其输出标记 y∈ {0,1},但线性回归模型产生的预测值$z=w^Tx+b
是实值,因此,我们需将实值
是实值,因此,我们需将实值
是实值,因此,我们需将实值z$转换为0/1值。最容易想到的联系函数g(·)当然是单位阶跃函数∶
y
=
{
0
,
z
<
0
;
如果预测值大于零就判为正例
0.5
,
z
=
0
;
小于零就判为反例
1
,
z
>
0
;
预测值为临界值零则可任意判别
y=\begin{cases} &0, & z<0;&\bf{如果预测值大于零就判为正例} \\ &0.5, & z=0; &\bf{小于零就判为反例} \\ &1, & z>0; &\bf{预测值为临界值零则可任意判别} \end{cases}
y=⎩
⎨
⎧0,0.5,1,z<0;z=0;z>0;如果预测值大于零就判为正例小于零就判为反例预测值为临界值零则可任意判别
但单位阶跃函数不连续,因此不能直接用作联系函数g(·)。于是我们希望找到能在一定程度上近似单位阶跃函数的替代函数,并希望它在临界点连续且单调可微。逻辑斯蒂函数(logistic function)正是这样一个常用的替代函数∶
y
=
1
1
+
e
−
z
y
=
1
1
+
e
−
(
w
T
x
+
b
)
y=\frac {1}{1+e^{-z}}\\ y=\frac {1}{1+e^{-(w^Tx+b)}}
y=1+e−z1y=1+e−(wTx+b)1

逻辑斯蒂(logistic function)函数形似s,是Sigmoid函数的典型代表,它将z值转化为一个接近0或1的y 值,并且其输出值在z=0附近变化很陡。
其对应的模型称为逻辑斯蒂回归(logistic regression)。需要特别说明的是,虽然它的名字是“回归”,但实际上却是一种分类学习方法。
逻辑斯蒂回归有很多优点∶
- 1)可以直接对分类可能性进行预测,将 y y y视为样本 x x x作为正例的概率;
- 2)无需事先假设数据分布,这样就避免了假设分布不准确所带来的问题;
- 3)是任意阶可导的凸函数,可直接应用现有数值优化算法求取最优解。
将
y
y
y 视为样本x属于正例的概率
p
(
y
=
1
∣
x
)
p(y=1|x)
p(y=1∣x),根据逻辑斯蒂函数很容易得到∶
y
=
1
1
+
e
−
(
w
T
x
+
b
)
→
p
(
y
=
1
∣
x
)
=
e
w
T
x
+
b
1
+
e
w
T
x
+
b
→
p
(
y
=
1
∣
x
)
=
1
1
+
e
w
T
x
+
b
y=\frac{1}{1+e^{-(w^Tx+b)}}\\ \rightarrow p(y=1|x)=\frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}\\ \rightarrow p(y=1|x)=\frac{1}{1+e^{w^Tx+b}}
y=1+e−(wTx+b)1→p(y=1∣x)=1+ewTx+bewTx+b→p(y=1∣x)=1+ewTx+b1
给定训练数据集
{
(
x
i
,
y
i
)
}
i
=
1
n
\{(x_i,y_i)\}^n_{i=1}
{(xi,yi)}i=1n,可通过"极大似然法"(maximum likelihood method)来估计w和b,即最大化样本属于其真实标记的概率(对数似然)∶
ℓ
(
w
,
b
)
=
∑
i
=
1
n
ln
p
(
y
i
∣
x
i
;
w
,
b
)
\ell(\boldsymbol{w}, b)=\sum_{i=1}^n \ln p\left(y_i \mid \boldsymbol{x}_i ; \boldsymbol{w}, b\right)
ℓ(w,b)=i=1∑nlnp(yi∣xi;w,b)
逻辑斯蒂回归中的因变量只有1和0(可理解为是/否、发生/不发生等)两种取值。
假设在 p p p个独立自变量 x 1 , x 2 , … , x p x1,x2,…,xp x1,x2,…,xp 的作用下,记y取1的概率为p=P(y=1|X),y取0的概率是1-p,取1和取0的概率之比为 p 1 − p \frac{p}{1-p} 1−pp,成为事件的优势比,对这个优势比取对数,也就是进行logistics变化,得到 l o g i t ( p ) = l n ( p 1 − p ) logit(p)=ln(\frac{p}{1-p}) logit(p)=ln(1−pp)。
令 l o g i t ( p ) = l n ( p 1 − p ) = z logit(p)=ln(\frac{p}{1-p})=z logit(p)=ln(1−pp)=z,则 p = 1 1 + e − z p=\frac{1}{1+e^{-z}} p=1+e−z1即为逻辑斯蒂函数。

建模步骤:
① 根据分析目的设置指标变量(因变量和自变量),然后收集数据,根据收集到的数据对特征再次进行筛选。
② y取1的概率是p=P(y=1|X),取0的概率是1-p。用 l n ( p 1 − p ) ln(\frac{p}{1-p}) ln(1−pp)和自变量列出线性回归方程,估计出模型中的回归系数。
③ 进行模型检验。模型有效性的检验指标有很多,最基本的是正确率,其次是混淆矩阵、roc曲线,ks值等。
④ 模型应用。输入自变量的取值就可以得到预测变量的值,或者根据预测变量的值去控制自变量的取值。
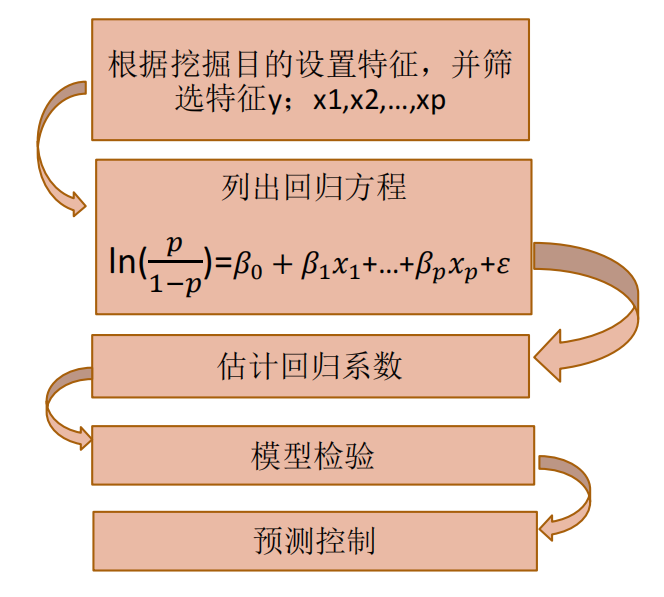
例题,某银行对降低贷款拖欠率的数据进行个逻辑斯的回归建模。

代码实现:
import pandas as pd
from sklearn.linear_model import LogisticRegression as LR
# 参数初始化
filename = './bankloan.xls'
data = pd.read_excel(filename)
x = data.iloc[:, :8].values
y = data.iloc[:, 8].values
lr = LR() # 建立逻辑回归模型
lr.fit(x, y) # 用筛选后的特征数据来训练模型
print('模型的平均准确度为:%s' % lr.score(x, y))






















 5652
5652











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










