003-1算法笔记【动态规划】矩阵相乘

问题

给定n个矩阵｛A1,A2,…,An｝，其中，Ai与Ai+1是可乘的，(i=1,2 ,…,n-1)。用加括号的方法表示矩阵连乘的次序，不同的计算次序计算量（乘法次数）是不同的，找出一种加括号的方法，使得矩阵连乘的次数最小。

例如：

              A1是A（5*10）的方阵；

              A2是A（10*100）的方阵；

              A3是A（100*2）的方阵；

那么有两种加括号的方法：

1. （A1A2）A3；
2.  A1（A2A3）；

     第一种方法的计算量：5*10*100+5*100*2=6000；

     第二种方法的计算量：10*100*2+5*10*2=2100；

     可以看出不同计算方法计算量差别很大。

分析

1. 两个矩阵相乘的计算量：

矩阵A(m,n)和B(n,k)的乘法运算次数为：m*n*k；

例如：A（3，2），B（2，4）, 可知总执行次数为：3*2*4=24.

2. 递推关系

将矩阵连乘 ·A_iA_i+1A_i+2……A_j 记作A[i:j]，1≤i≤j≤n，用m[i][j]表示矩阵连乘 A[i:j]的最少计算量，则原问题的最优值为m[1][n]。

a. 当i=j时，A[i:j]=Ai，因此，m[i][i]=0，i=1,2,…,n

b. 当i<j时，假设A[i:j]在第k位置上找到最优解，i <= k < j, 则问题变成了两个子问题：(A_iA_i+1…A_k) ,(A_k+1…A_j ), 用s[i][j]=k记录下最优划分位置。有递推关系：
m[i][j]=m[i][k]+m[k+1][j]+ p[i-1]*p[k]*p[j]
k的位置有j-i个可能。因此，k是这j-i个位置使计算量达到最小的那个位置。

c. 综上，有递推关系如下：

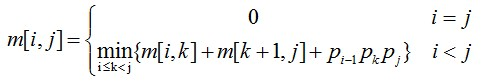
3. 最优子结构

用m[i][j]表示矩阵连乘 ·A_iA_i+1A_i+2……A_j 的最优解

假设在第k位置上找到最优解，则问题变成了两个子问题：(A_iA_i+1…A_k) ,(A_k+1…A_j ), 用s[i][j]=k记录下最优划分位置

那么两个子问题对应的最优值变成m[i][k],m[k+1][j]

子问题合并：m[i][j]=m[i][k]+m[k+1][j]+p[i]*p[k+1]*p[j]

暴力

递归实现

直接递归

递归不等式：

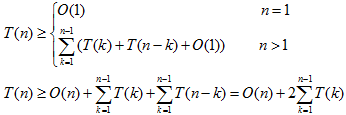
用数学归纳法可以证明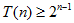，指数增长。

带备忘录的递归

#include<iostream>
#include<cstring> 
using namespace std;

const int size=20;
int p[size]={30,35,15,5,10,20,25};//储存Ai的尺寸：A1，A2，...An-1的行数，An的列数
int m[size][size];//最优解
int s[size][size];//分割位置
int n=6;

//带备忘录的递归
int recur_helper(int i,int j);
void getChain_recur(int i,int j){
 memset(m,0,sizeof(m));
 memset(s,0,sizeof(s));//初始化数组
 recur_helper(i,j);
}
int recur_helper(int i,int j){
 if(m[i][j]>0)return m[i][j];//已经计算过了
 if(i==j)return 0;

  
 int min_cost=recur_helper(i,i)+recur_helper(i+1,j)+p[i-1]*p[i]*p[j];
 s[i][j]=i;
 for(int k=i+1;k<j;k++){
     int tmp=recur_helper(i,k)+recur_helper(k+1,j)+p[i-1]*p[k]*p[j];
     //更优的分割位置
     if(tmp<min_cost){
         s[i][j]=k;
         min_cost=tmp;
     }
 }
 m[i][j]=min_cost;
 return min_cost;
}
void print(int i,int j)
{
 if(i == j)
 {
 	cout<<"A["<<i<<"]";
 	return;
 }
 cout<<" (";
 //k=s[i][j],划分为（Ai...Ak）(Ak+1...Aj)
 print(i,s[i][j]);
 print(s[i][j]+1,j);
 cout<<")";
}

int main()
{
 // cout<<"请输入矩阵的个数n : "<<endl;
 // cin>>n;

 // cout<<"请依次输入每个矩阵的行数和最后一个矩阵的列数："<<endl;
 // for(int i=0;i<=n;i++)
 // 	cin>>p[i];
 cout<<endl<<"递归:"<<endl;
 getChain_recur(1,n);
 print(1,n);
 cout<<endl;
 cout<<"最小计算量的值为："<<m[1][n]<<endl;

 return 0;
}

备忘录算法耗时O(n³)，将直接递归算法的计算时间从 2ⁿ 降至O(n³)。

动态规划实现

s[i][j]记录括号的位置，表示连乘(A_i…A_j)，例如

#include<iostream>
#include<cstring> 
using namespace std;
 
const int size=20;
int p[size]={30,35,15,5,10,20,25};//储存Ai的尺寸：A1，A2，...An-1的行数，An的列数
int m[size][size];//最优解
int s[size][size];//分割位置
int n=6;

//动态规划
void getChain_dp()
{
	int i,r,j,k;
	memset(m,0,sizeof(m));
	memset(s,0,sizeof(s));//初始化数组
	for(r=2;r<=n;r++)//矩阵连乘的规模为r 
	{
		for(i=1;i<=n-r+1;i++)//遍历每一组的起点:A1A2,...An-1An; A1A2A3,A4A5A6,....;
		{
			j=i+r-1;//每一组的终点
            //在[i,j]中寻找最优分割位置k，使m[i][j]=m[i][k]+m[k+1][j]+p[i-1]p[k]p[j]最小

			m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];//初始划分:k=i, Ai (Ai+1...Aj),避开边界A[0]
			s[i][j]=i;//s[][]存储子问题的分割位置
			for(k=i+1;k<j;k++)//在[i+1,j]寻找最优分割位置k
			{
				int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
				if(t < m[i][j])
				{
					m[i][j]=t;
					s[i][j]=k;
				}
			}
		}
	}
}
//带备忘录的递归
int recur_helper(int i,int j);
void getChain_recur(int i,int j){
	memset(m,0,sizeof(m));
	memset(s,0,sizeof(s));//初始化数组
    recur_helper(i,j);
}
int recur_helper(int i,int j){
    if(m[i][j]>0)return m[i][j];//已经计算过了
    if(i==j)return 0;

     
    int min_cost=recur_helper(i,i)+recur_helper(i+1,j)+p[i-1]*p[i]*p[j];
    s[i][j]=i;
    for(int k=i+1;k<j;k++){
        int tmp=recur_helper(i,k)+recur_helper(k+1,j)+p[i-1]*p[k]*p[j];
        //更优的分割位置
        if(tmp<min_cost){
            s[i][j]=k;
            min_cost=tmp;
        }
    }
    m[i][j]=min_cost;
    return min_cost;
}
void print(int i,int j)
{
	if(i == j)
	{
		cout<<"A["<<i<<"]";
		return;
	}
	cout<<" (";
    //k=s[i][j],划分为（Ai...Ak）(Ak+1...Aj)
	print(i,s[i][j]);
	print(s[i][j]+1,j);
	cout<<")";
}
 
int main()
{
	// cout<<"请输入矩阵的个数n : "<<endl;
	// cin>>n;

	// cout<<"请依次输入每个矩阵的行数和最后一个矩阵的列数："<<endl;
	// for(int i=0;i<=n;i++)
	// 	cin>>p[i];
    cout<<endl<<"递归:"<<endl;
    getChain_recur(1,n);
    print(1,n);
    cout<<endl;
	cout<<"最小计算量的值为："<<m[1][n]<<endl;

    cout<<"动态规划："<<endl;
	getChain_dp(); 
	print(1,n);
	cout<<endl;
	cout<<"最小计算量的值为："<<m[1][n]<<endl;

	return 0;
}

迭代算法的运行过程如下图所示：

 当R=2时，先迭代计算出：
 
 m[1:2]=m[1:1]+m[2:2}+p[0]*p[1]*p[2]；

 m[2:3]=m[2:2]+m[3:3]+p[1]*p[2]*p[3];

 m[3:4]=m[3:3]+m[4][4]+p[2]*p[3]*p[4];

 m[4:5]=m[4:4]+m[5][5]+p[3]*p[4]*p[5];

 m[5:6]=m[5][5]+m[6][6]+p[4]*p[5]*p[6]的值；

 当R=3时，迭代计算出：

 m[1:3]=min(m[1:1]+m[2:3]+p[0]*p[1]*p[3],m[1:2]+m[3:3]+p[0]*p[2]*p[3]);

 m[2:4]=min(m[2:2]+m[3:4]+p[1]*p[2]*p[4],m[2:3]+m[4:4]+p[1]*p[3]*p[4]);

 ......

 m[4:6]=min(m[4:4]+m[5:6]+p[3]*p[4]*p[6],m[4:5]+m[6:6]+p[3]*p[5]*p[6]);

 ......

时间复杂度： 填二维数组Ω（n），每填一个需要线性扫描一次O(n)，T(n)=Ω（n）* O(n) = O(n³)。
空间复杂度：S(n) = O(n²)

运行截图：

凸三角形剖分

凸三角形剖分与矩阵相乘的对应：

递归树

对比矩阵连乘问题，发现两个递归树是同构的：