Fidelity指标

一、纯视觉模型

ViT

1 transformer应用于视觉挑战：

2 vit 架构：

二、多模态模型

CLIP

sos令牌和eos令牌

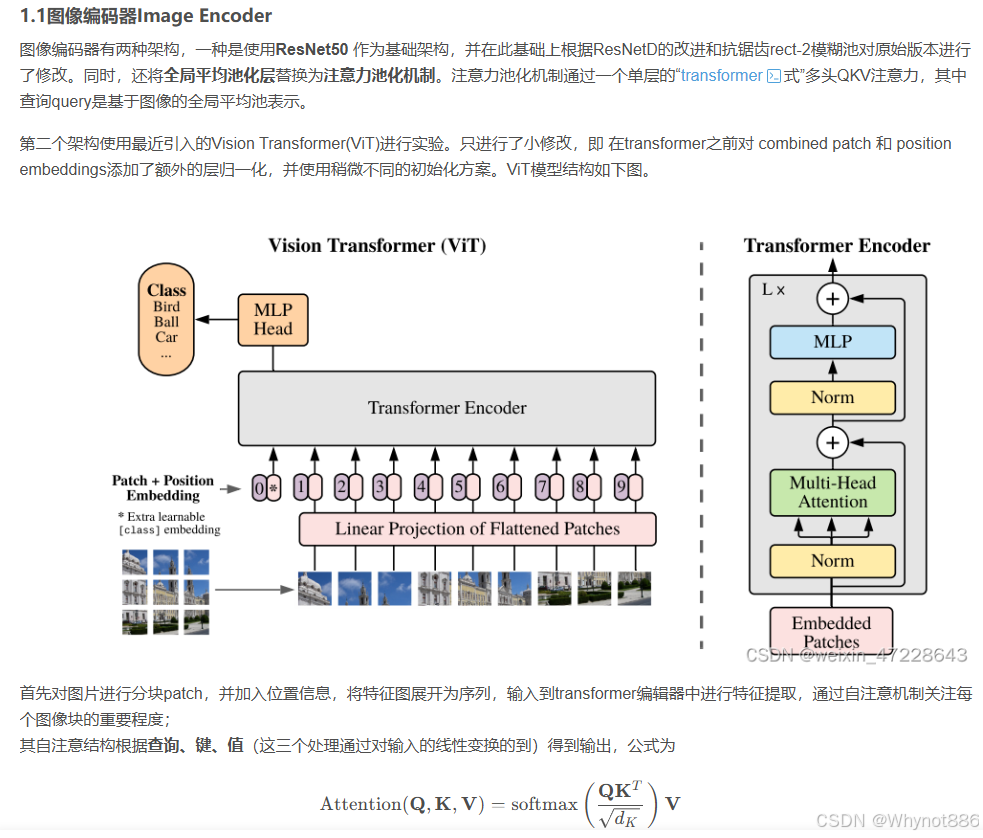
在 CLIP（Contrastive Language-Image Pre-training）模型中，通常没有明确规定 SOS 和 EOS token 必须设为某个固定的具体数值。不过 CLIP 的文本编码器在处理文本时，一般会遵循以下的常见做法：
SOS（Start of Sequence）：CLIP 的文本编码器基于 Transformer 架构，使用小写字节对编码（BPE）表示文本时，SOS 标记用来表示文本序列的开始。它更多是一种标记符号，在实际的嵌入向量表示中，会被映射为一个特定的向量，但这个向量的具体数值取决于模型的初始化和训练过程。
EOS（End of Sequence）：CLIP 模型将 EOS 标记上 Transformer 最高层的激活函数（层归一化）的结果，用作文本的特征表示，然后线性投影到多模态嵌入空间中。同样，EOS 标记对应的向量值也是在模型训练过程中动态确定的，没有一个固定的先验数值。

主要代码

其中只有text-encoder的输出需要投影，visual 不用，投影使用eos token的值，这个叫做文本投影
text是一个所有字符对应数字的数组

**## Q-Former
Q-Former（Query Transformer）是在视觉 - 语言模型领域提出的一种架构，常与大型语言模型（LLM）结合使用，典型的应用是在BLIP - 2模型中。下面详细介绍Q-Former的原理。

背景与设计动机

在视觉 - 语言模型中，如何有效地将视觉信息与语言信息进行融合是一个关键问题。传统方法可能直接将视觉特征输入到语言模型中，但由于视觉特征和语言特征的模态差异较大，以及大型语言模型参数量巨大、计算成本高，直接融合的效果和效率都存在一定问题。Q - Former的设计旨在作为一个中间桥梁，高效地将视觉信息转换为适合语言模型处理的格式。

原理详解

核心组件与结构

• 可学习的查询向量（Learnable Queries）：Q - Former引入了一组可学习的查询向量（Queries），这些查询向量的数量通常远小于视觉特征的数量。例如，在BLIP - 2中，使用了32个查询向量。这些查询向量在训练过程中会不断学习，以捕捉视觉特征中与语言相关的重要信息。
• Transformer架构：Q - Former基于Transformer架构构建，它由多个Transformer层组成。在这些层中，主要包含多头自注意力机制（Multi - Head Self - Attention）和跨注意力机制（Cross - Attention）。

信息交互过程

• 跨注意力机制融合视觉信息：在Q - Former中，跨注意力机制用于将可学习的查询向量与视觉特征进行交互。具体来说，查询向量作为查询（Query），视觉特征作为键（Key）和值（Value），通过跨注意力机制计算得到查询向量与视觉特征之间的注意力分数，然后根据这些分数对视觉特征进行加权求和，从而将视觉信息融入到查询向量中。可以表示为：
  [ \text{CrossAttention}(Q, K_{vis}, V_{vis})=\text{softmax}(\frac{QK_{vis}^T}{\sqrt{d_k}})V_{vis} ]
  其中 (Q) 是可学习的查询向量，(K_{vis}) 和 (V_{vis}) 分别是视觉特征的键和值矩阵，(d_k) 是键向量的维度。
• 自注意力机制提炼特征：在经过跨注意力机制融合视觉信息后，查询向量会通过多头自注意力机制进行信息的提炼和整合。自注意力机制允许查询向量之间相互交互，捕捉它们之间的依赖关系，进一步提取和组织与视觉相关的语义信息。

与大型语言模型的结合

• 生成语言友好的特征：经过Q - Former处理后，可学习的查询向量已经融合了视觉信息并进行了特征提炼，这些查询向量可以被视为一种语言友好的视觉特征表示。
• 输入到语言模型：将这些经过处理的查询向量作为额外的输入序列，与文本输入一起输入到大型语言模型中。由于查询向量的数量相对较少，这样可以在不显著增加计算成本的情况下，将视觉信息有效地传递给语言模型，从而实现视觉 - 语言的联合建模。

优势

• 高效信息融合：通过可学习的查询向量和跨注意力机制，能够高效地将视觉信息融入到语言处理流程中，避免了直接将大量视觉特征输入语言模型带来的计算和融合难题。
• 降低计算成本：使用少量的查询向量代替大量的视觉特征与语言模型交互，大大降低了计算成本，使得在资源有限的情况下也能实现有效的视觉 - 语言模型训练和推理。

CLIP原理

CLIP（Contrastive Language - Image Pretraining）是OpenAI开发的一种多模态模型，能够学习图像和文本之间的关联。以下将从背景、核心原理、训练过程、推理过程几个方面详细介绍CLIP的原理。

背景

传统的图像分类模型通常是针对特定的任务进行训练，需要大量的标注数据，并且只能处理预定义的类别。而CLIP的目标是实现更通用的图像理解，通过学习图像和文本之间的关联，使得模型能够根据任意文本描述来识别图像。

核心原理

CLIP的核心思想是通过对比学习来学习图像和文本之间的语义对齐。它包含两个编码器：图像编码器和文本编码器。

• 图像编码器：将输入的图像编码为一个固定长度的特征向量。常见的图像编码器可以基于卷积神经网络（CNN），如ResNet，或者基于Transformer架构，如ViT（Vision Transformer）。
• 文本编码器：将输入的文本（如一段描述图像的自然语言句子）编码为一个固定长度的特征向量。通常使用基于Transformer的语言模型，如BERT的变体。

CLIP的训练目标是使得图像和与之对应的文本在特征空间中的距离尽可能小，而与不对应的图像 - 文本对的距离尽可能大。

训练过程

数据准备

收集大量的图像 - 文本对数据，这些文本可以是对图像的自然语言描述。例如，一张猫的图片对应的文本可以是“一只可爱的猫坐在沙发上”。

特征编码

• 对于每一个图像 - 文本对，将图像输入到图像编码器中，得到图像特征向量 (I)；将文本输入到文本编码器中，得到文本特征向量 (T)。
• 对特征向量进行归一化处理，使得它们的模长为1，这样可以简化后续的相似度计算。

对比损失计算

• 假设一个批次中有 $N$ 个图像 - 文本对。对于每一个图像特征向量 $I_i$（$i=1,2,\cdots ,N$），计算它与所有文本特征向量 (T_j)（$j=1,2,\cdots ,N$）的相似度。相似度通常使用点积来计算，即 $s(I_i,T_j)=I_i^T{T}_j$。
• 构建一个 $N\times N$ 的相似度矩阵 $S$，其中 $S_{ij}=s(I_i,T_j)$。矩阵的对角线元素 $S_{ii}$ 表示正确的图像 - 文本对的相似度，非对角线元素 $S_{ij}(i\ne j)$ 表示错误的图像 - 文本对的相似度。
• 使用对比损失（Contrastive Loss）来训练模型。CLIP使用的是InfoNCE（Info - Noise Contrastive Estimation）损失，其目标是最大化正确的图像 - 文本对的相似度，同时最小化错误的图像 - 文本对的相似度。具体公式如下：
  • 从图像到文本的损失：$L_{i2t}=-\log \frac{\exp (S_{ii}/\tau )}{{\sum }_{j=1}^N\exp (S_{ij}/\tau )}$
  • 从文本到图像的损失：$L_{t2i}=-\log \frac{\exp (S_{ii}/\tau )}{{\sum }_{j=1}^N\exp (S_{ji}/\tau )}$
  • 总损失：$L=\frac{1}{2}(L_{i2t}+L_{t2i})$
    其中 $\tau$ 是一个温度参数，用于控制相似度的分布。

模型优化

使用优化算法（如Adam）最小化总损失 (L)，不断更新图像编码器和文本编码器的参数，使得模型能够学习到图像和文本之间的语义关联。

推理过程

图像分类

• 给定一个图像和一组候选的文本标签（如“猫”、“狗”、“汽车”等）。
• 使用训练好的图像编码器对图像进行编码，得到图像特征向量 (I)；使用文本编码器对每个文本标签进行编码，得到文本特征向量 $T_1,T_2,\cdots ,T_k$。
• 计算图像特征向量与每个文本特征向量的相似度 $s(I,T_i)$（$i=1,2,\cdots ,k$）。
• 选择相似度最高的文本标签作为图像的分类结果。

图像检索

• 给定一个文本查询（如“一张美丽的风景照片”）和一个图像数据库。
• 使用文本编码器对文本查询进行编码，得到文本特征向量 (T)；使用图像编码器对数据库中的每个图像进行编码，得到图像特征向量 $I_1,I_2,\cdots ,I_n$。
• 计算文本特征向量与每个图像特征向量的相似度 $s(T,I_j)$（$j=1,2,\cdots ,n$）。
• 根据相似度对图像进行排序，返回相似度最高的若干张图像作为检索结果。

Flamingo

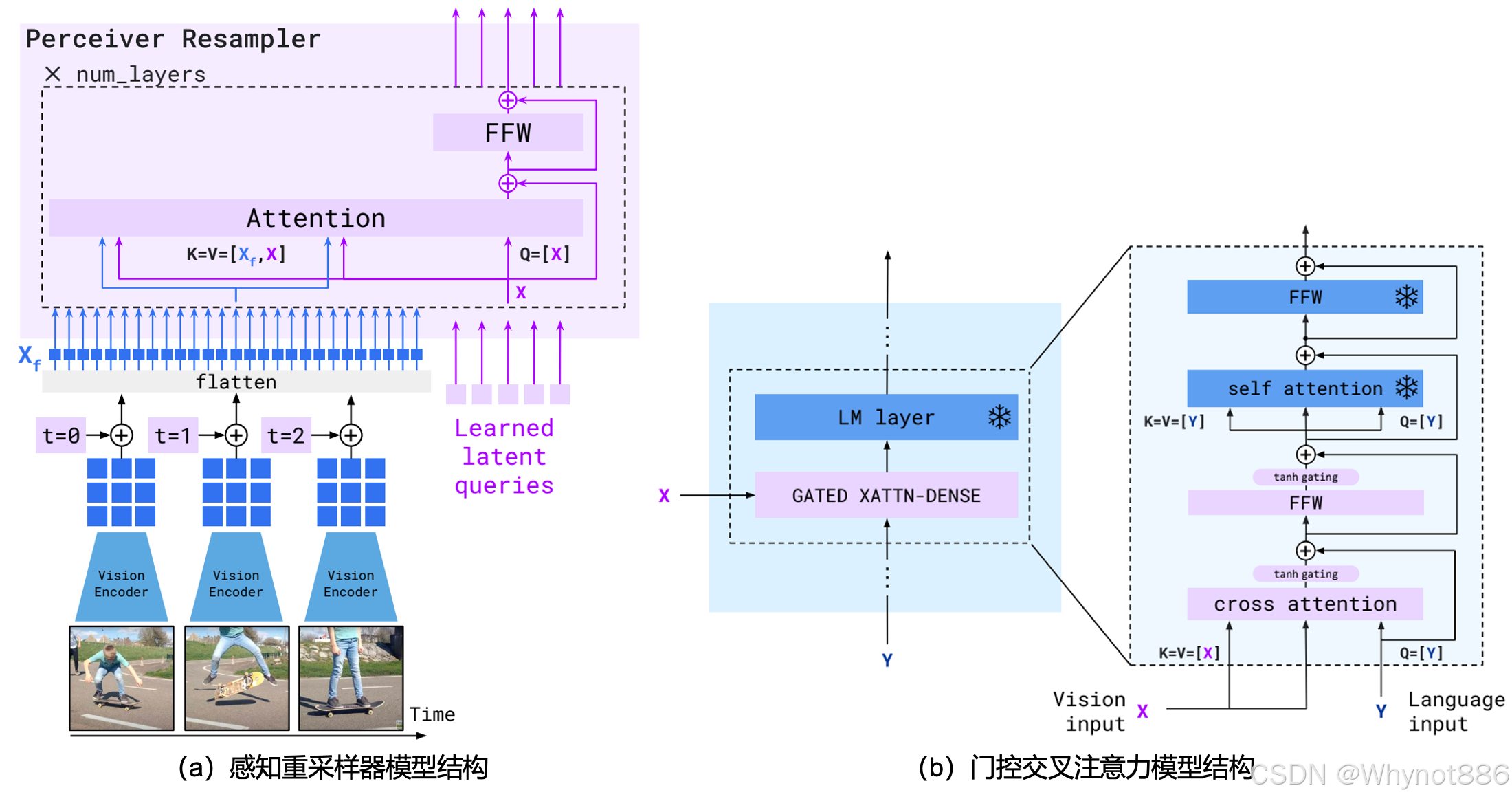
冻结了视觉模型和LLM，使用一个感知重采样器来将视觉token padding到固定长度，然后使用门控交叉注意力机制来进行视觉token和文本token的融合。
网络架构图：

Perceiver Resampler：
这个重采样就是和q-former一样的使用可学习向量来通过交叉注意力机制来整合图像特征，输出固定大小64个视觉token，然后将这64个tokens过一个可学学习的交叉注意力来将视觉信息融入到冻结的LLM中

BLIP

blip任务使用和CLIP同样的带噪声的大规模图文对数据集一下子就完成了三个视觉任务或者不同角度的关联任务的预训练工作，而且他还开创了一个让模型自己来过滤自己数据集的方式对数据集进行筛选和去噪，除了原本的CLIP里面的text encoder和image encoder之外，还加入了一个多模态的编码器和一个多模态的解码器，可以同时训练4个模型

• 网络架构：
• 
  
  

介绍到这里可以大致捋一下 BLIP 的训练思路：先使用含有噪声的网络数据训练一遍 BLIP，再在 COCO 数据集上进行微调以训练 Captioner 和 Filter，然后使用 Filter 从原始网络文本和合成文本中删除嘈杂的字幕，得到干净的数据。最后再使用干净的数据训练一遍得到高性能的 BLIP。
BLIP其实最终训练出来就只有一个文本encoder和一个多模态encoder，其中图像encoder和两个多模态都是共享的参数

BLIP2

BEIT v3

1 背景

当前的视觉语言基础模型通常多任务处理其他预训练目标(如图像-文本匹配)，使得扩展不友好且效率低下。相比之下，我们只使用一个预训练任务，即mask-then-predict，来训练通用的多模态基础模型。通过将图像视为一门外语(即英语)，我们以相同的方式处理文本和图像，没有根本的建模差异。因此，图像-文本对被用作“平行句”，以学习模态之间的对齐。我们还表明，简单而有效的方法学习强可转移表征，在视觉和视觉语言任务上都取得了最先进的性能。显著的成功证明了生成式预训练的优越性[DCLT19, BDPW22]。

第三，模型规模和数据规模的普遍扩大提高了基础模型的泛化质量，使我们可以将其转移到各种下游任务中。我们遵循这一理念，将模型规模扩大到数十亿个参数。此外，我们在实验中扩大了预训练数据的大小，而只使用公开可访问的学术资源。虽然没有使用任何私人数据，但我们的方法比依赖内部数据的最先进的基础模型要好得多。此外，将图像作为一门外语来处理，可以直接重用为大规模语言模型预训练而开发的管道。

在这项工作中，我们利用上述思想预训练了一个通用的多模态基础模型BEIT-3。我们通过对图像、文本和图像-文本对执行屏蔽数据建模来预训练多路变压器。在预训练过程中，我们随机屏蔽一定比例的文本标记或图像补丁。自监督学习的目标是恢复给定损坏输入的原始令牌(即文本令牌或视觉令牌)。该模型是通用的，因为它可以重新用于各种任务，而不管输入方式或输出格式如何。

如图1和表1所示，BEIT-3在广泛的视觉和视觉语言任务中实现了最先进的迁移性能。我们在广泛的下游任务和数据集上评估了BEIT-3，即对象检测(COCO)、实例分割(COCO)、语义分割(ADE20K)、图像分类(ImageNet)、视觉推理(NLVR2)、视觉问答(VQAv2)、图像字幕(COCO)和跨模态检索(Flickr30K, COCO)。具体来说，尽管我们只使用公共资源进行预训练和微调，但我们的模型优于之前的强基础模型[YWV+22, ADL+22, YCC+21]。该模型也获得了比专门模型更好的结果。此外，BEIT-3不仅在视觉语言任务上表现良好，而且在视觉任务(如目标检测、语义分割)上也表现良好。

2 模型架构

大模型微调方法

lora

需要微调的矩阵：
Transformer的权重矩阵包括Attention模块里用于计算query, key, value的Wq，Wk，Wv以及多头attention的Wo和MLP层的权重矩阵，LoRA只应用于Attention模块中的4种权重矩阵，并且通过消融实验发现同时调整 Wq 和 Wv 会产生最佳结果，因此，默认的模块名基本都为 Wq 和 Wv 权重矩阵。

代码

prefix tuning

1 首先arrange一个数组，长度为虚拟token数目
2 建立一个embedding 为 nn.embedding(虚拟token个数，层数*2（每层的key和value）*隐状态维度)
3 然后将embedding分为key和value，加在不同的层上面，把q和k拼接到最前面，在每一层计算时都需要更新参数

P-tuning

在原本的序列前面，中间或者后面插入可学习的embedding，只不过在embedding之后需要使用一个lstm和mlp

P-tuningv2

和prefix tuning相同，只不过移除了重参数，即mlp，而且从自然语言生成任务转变为自然语言理解任务

三、纯语言大模型LLM

Llama

LaMA模型摒弃了Transformer Encoder部分，专注于Decoder结构，使其更适合文本生成任务。Decoder层由一系列堆叠的Decoder Blocks构成，每个Block内部又包含多头自注意力机制（Multi-Head Self-Attention，MHSA）和前馈神经网络（Feed-Forward Network，FFN）两个主要组件。

Pre-Normalization（Pre-Norm，层前归一化）：与原始Transformer的Post-Norm（层后归一化）不同，LLaMA采用了Pre-Norm策略，即将层归一化层置于自注意力和前馈神经网络层之前。这种方法有助于稳定训练过程，尤其是在深层网络中，可以缓解梯度消失或爆炸的问题。

transformer：

层RMSNorm（Root Mean Square Layer Normalization，均方根层归一化）：LLaMA采用了RMSNorm作为一种替代或补充的归一化方案，相比于Layer Normalization，RMSNorm依据均方根准则调整输入特征，以适应大规模模型训练时的动态范围问题。
这里列出LayerNorm与RMSNorm归一化的表达式：

GLU:

旋转位置编码

Bert和GPT的区别

一、模型基础与架构

BERT：

全称：Bidirectional Encoder Representations from Transformers。

架构：基于Transformer的编码器部分进行堆叠构建，通过预训练和微调两个阶段来生成深度的双向语言表征。

特点：使用了Transformer的encoder部分，通过双向语言模型预训练来学习上下文相关的词表示。

GPT：

全称：Generative Pre-trained Transformer。

架构：基于Transformer的解码器部分，通过自回归语言模型预训练来学习生成连贯文本的能力。

特点：采用了自回归语言模型的预训练方式，逐步生成下一个词语，以此生成连贯的文本。

二、训练方式与任务

BERT：

训练任务：主要包括掩码语言模型（Masked Language Model, MLM）和下一句预测（Next Sentence Prediction, NSP）。

MLM：在输入序列中随机掩盖一些词语，要求模型预测这些被掩盖的词语。

NSP：判断两个句子是否是连续的文本序列。

训练方式：双向预训练，同时考虑前后文信息。

GPT：

训练任务：自回归语言模型预训练。

训练方式：单向预训练，从左到右生成文本，只能依赖已生成的上文来预测下一个词语。

三、上下文理解能力

BERT：

由于采用了双向语言模型，BERT能够同时考虑前后文信息，因此在理解整个句子或段落时表现出色。

适用于需要理解整个文本的任务，如分类、命名实体识别和句子关系判断等。

GPT：

作为单向模型，GPT在生成文本时只能依赖已生成的上文，因此在处理需要理解整个文本的任务时可能表现不足。

但其生成文本的能力较强，适用于各种生成式的NLP任务。

四、应用领域

BERT：

因其强大的上下文理解能力，BERT在多种NLP任务中都有广泛应用，如情感分析、问答系统、命名实体识别等。

GPT：

GPT的强项在于生成连贯、有逻辑性的文本，因此在文本生成、机器翻译、对话系统等任务中表现出色。
① Transformer使用自注意力机制进行编码和解码，能够处理长序列数据；

② BERT使用掩码语言模型和下一句预测任务进行训练，能够在不同的自然语言处理任务中取得良好的效果；

③ GPT大模型是一种基于自回归模型的语言模型，能够生成连贯、自然的文本内容。

BERT是一种基于Transformer架构的预训练语言模型它使用大量未标记的文本进行预训练，然后使用标记的数 据进行微调。全称Bidirectional Encoder Representations from Transformers。
BERT的特点在于它可以双向地处理输入序列，从而更好地捕捉上下文中的语义信息。BERT模型的输入是两个序列，一个序列作为模型的输入，另一个序列作为模型的输出，模型需要判断这两个序列是否相互关联。这个过程被称为下一句预测任务。此外，BERT还使用了掩码语言模型，其中模型在输入序列中随机地掩盖一些单词，并要求模型预测这些被掩盖的单词。这个训练任务有助于模型更好地理解语言中的上下文信息。

什么是掩码技术？专业术语叫做masking。

简单理解就是，这种masking的训练技巧可以理解为在做一种语言填空练习，就像我们在学校里做英语完型填空题一样。在这种练习中，Bert会随机选择一些文本中的词汇并进行屏蔽，就像把填空题的空格用一条横线代替一样。然后，Bert需要根据上下文和语法规则来猜测被屏蔽的词汇，就像我们需要根据句子的意义和语法规则来猜测填空题的答案一样。经过不断的反复练习，Bert就变成了一个无情的做题狂魔。这样Bert就能更好地理解和表示文本的含义。此外，由于在屏蔽词汇时需要随机选择，这也可以帮助Bert更好地应对文本中出现的不同词汇和语言变化，增强其泛化能力。

强化学习方法

1 SFT 和 强化学习的区别

大模型幻觉

大模型幻觉（Hallucination in Large Language Models）指的是大语言模型在生成内容时，输出一些与事实不符、无中生有或者逻辑混乱的信息，就好像模型“凭空想象”出了这些内容，常见于文本生成、问答系统等场景。以下为你详细介绍其表现形式、产生原因和应对策略。

表现形式

• 事实性错误：模型输出的内容与客观事实相悖。例如在回答历史问题时，可能会编造不存在的历史事件、人物关系或时间节点；在提供科学知识时，给出错误的定理、公式或概念。比如声称“地球是平的”，或者说“牛顿是因为被苹果砸中脑袋才发现了万有引力定律，且该定律只适用于地球上”（实际上万有引力定律是普遍适用的）。
• 无中生有：生成一些现实中并不存在的信息。比如在描述一部影视作品时，提及不存在的情节、角色；在介绍一个城市时，虚构出当地并不存在的景点、建筑或节日。例如，称某部电影中有一个名为“超级时空穿越大战”的情节，但实际上该电影里并没有。
• 逻辑混乱：输出的内容在逻辑上存在矛盾或不合理之处。可能在一段话中前后观点不一致，或者推理过程不符合常理。例如，前面说“所有的猫都会游泳”，后面又说“这只猫不会游泳，但它属于所有猫的范畴”。

产生原因

• 训练数据问题
  • 数据偏差：训练数据可能存在偏差，包含不完整、不准确或有偏见的信息，导致模型学习到错误的知识。例如，如果训练数据中关于某个领域的信息主要来自于非权威来源，模型可能会输出错误的结论。
  • 数据稀疏：对于某些特定领域或罕见事件，训练数据可能非常有限，模型难以学习到全面准确的知识，从而容易产生幻觉。
• 模型架构和学习机制
  • 泛化过度：模型在学习过程中可能会过度泛化，将一些局部的规律推广到不适用的情况，从而生成错误的内容。
  • 缺乏真实世界感知：大语言模型本质上是基于文本数据进行训练的，缺乏对真实世界的直接感知和理解。它只能根据训练数据中的模式进行生成，而无法判断生成内容的真实性。
• 优化目标和局限性
  • 追求流畅性和连贯性：模型的优化目标通常侧重于生成流畅、连贯的文本，而不是保证内容的真实性。为了满足流畅性要求，模型可能会编造一些信息来使输出看起来更自然。

应对策略

• 数据层面
  • 数据清洗和验证：对训练数据进行严格的清洗和验证，去除错误、虚假和有偏见的信息，确保数据的质量。
  • 引入外部知识：将外部知识库（如维基百科、专业数据库等）与模型相结合，让模型在生成内容时能够参考准确的知识。
• 模型层面
  • 模型优化和正则化：通过改进模型的架构和训练方法，如增加正则化项、调整优化算法等，减少模型的过拟合和泛化过度问题。
  • 后处理和验证机制：在模型生成内容后，使用额外的验证模块对输出进行检查和修正，例如利用知识图谱进行事实核查。
• 交互层面
  • 用户反馈和纠正：鼓励用户对模型输出的错误内容进行反馈，利用用户反馈来不断改进模型。
  • 提示工程：通过设计更清晰、准确的提示，引导模型生成更可靠的内容。例如，在提问时提供更多的背景信息和约束条件。

Transformer中FFN为什么要先升维再降维度，FFN的作用是什么？

Llama1 2 3的区别

llama1

数据集：模型训练数据集使用的都是开源的数据集。
模型结构：原始的Transformer由编码器（Encoder）和解码器（Decoder）两个部分构成。同时Encoder和Decoder这两部分也可以单独使用，llama是基于Transformer Decoder的架构，在此基础上上做了以下改进：
（1）llama将layer-norm 改成RMSNorm(Root Mean square Layer Normalization)，并将其移到input层，而不是output层。
（2）采用SwiGLU激活函数。
（3）采用RoPE位置编码。

分词器：分词器采用BPE算法，使用 SentencePiece 实现，将所有数字拆分为单独的数字，并使用字节来分解未知的 UTF-8 字符。词表大小为 32k 。
优化器：AdamW,是Adam的改进，可以有效地处理权重衰减，提供训练稳定性。
learning rate：使用余弦学习率调整 cosine learning rate schedule，使得最终学习率等于最大学习率的10%，设置0.1的权重衰减和1.0的梯度裁剪。warmup的step为2000，并根据模型的大小改变学习率和批处理大小。
模型效果：llama-13B(gpt-3 1/10大小)在多数benchmarks上超越gpt-3 (175B)。在规模较大的端，65B参数模型也与最好的大型模型（如Chinchilla或PaLM-540B）也具有竞争力。

llama2

由Meta AI 发布，包含 7B、13B 、 34B、70B 四种参数规模的基座语言模型,除了34B其他模型均以开源。开源且免费可商用
数据集：模型训练数据集使用的都是开源的数据集，相比上一代的训练数据增加了 40%，达到了增至2万亿个token，训练数据中的文本来源也更加的多样化。Llama 2对应的微调模型是在超过100万条人工标注的数据下训练而成。（但是Llama 2语料库 仍以英文（89.7%）为主，而中文仅占据了其中的 0.13%。这导致 Llama 2 很难完成流畅、有深度的中文对话。）
模型结构：
（1）Llama 2与Llama 1的主要结构基本一致同样也是在transformer decoder结构上做了3大改进：将layer-norm改成RMSNorm(Root Mean square Layer Normalization)，并将其移到input层，而不是output层、采用SwiGLU激活函数、采用旋转位置嵌入RoPE。
（2）Llama 2上下文长度由之前的2048升级到4096，可以理解和生成更长的文本。
（3）7B和13B 使用与 LLaMA 相同的架构，34B和70B模型采用分组查询注意力（GQA）。
优化器：AdamW 其中β1=0.9，β2=0.95，eps=10−5。
learning rate：使用cosine learning rate schedule，使得最终学习率等于最大学习率的10%，设置0.1的权重衰减和1.0的梯度裁剪。warmup的step为2000，并根据模型的大小改变学习率和批处理大小。
分词器：分词器采用BPE算法，使用 SentencePiece 实现，将所有数字拆分为单独的数字，并使用字节来分解未知的 UTF-8 字符。词汇量为 32k token。
模型效果：从模型评估上看，Llama 2在众多的基准测试中，如推理、编程、对话能力和知识测验上，都优于Llama1和现有的开源大模型。Llama 2 70B在MMLU和GSM8K上接近GPT-3.5（OpenAI，2023），但在编码基准方面存在显著差距。Llama 2 70B的结果在几乎所有基准上都与PaLM（540B）（Chowdhery et al.，2022）不相上下或更好。Llama 2 70B与GPT-4 和PaLM-2-L在性能上仍有很大差距。

llama3

数据集：llama2相比上一代的训练数据增加了 40%，达到了2T个token，Llama 3 的预训练数据集增加至15T，这些数据都是从公开来源收集的高质量数据集（依旧强调高质量的训练数据集至关重要）。其中包括了4 倍以上的代码 token 以及 30 种语言中 5% 的非英语 token（这意味着LLAMA-3在代码能力以及逻辑推理能力的性能将大幅度提升）。微调数据包括公开可用的指令数据集以及超过1000万个人工注释的示例。预训练和微调数据集均不包含元用户数据。（主要还是以英语为主了，中文占比依旧很低，前面测试也可以看出来) 。通过开发一系列数据过滤流程：包括使用启发式筛选器、NSFW 筛选器、语义重复数据删除方法和文本分类器
来预测数据质量。以及使用 Llama 2 为 Llama 3 提供支持的文本质量分类器生成训练数据。
模型结构：Llama 3 中选择了相对标准的纯解码器decoder-only transformer架构，总体上与 Llama 2 相比没有重大变化。在 Llama 2 中只有34B,70B使用了分组查询注意 (GQA)，但为了提高模型的推理效率，Llama 3所有模型都采用了GQA。
分词器：与Llama 2不同的是，Llama 3将tokenizer
由sentencepiece换成tiktoken,词汇量从 的32K增加到 128K，增加了 4 倍。更大的词汇库能够更高效地编码文本，增加编码效率，可以实现更好的下游性能。不过这也会导致嵌入层的输入和输出矩阵尺寸增大，模型参数量也会增大。
序列长度：输入上下文长度从 4096（Llama 2）和 2048（Llama 1）增加到 8192。但相对于GPT-4 的 128K来说还是相当小。
缩放定律：对于像 8B 参数这样“小”的模型来说，扩展法则
Chinchilla 最优训练计算量对应于 ~200B Tokens，但是Meta使用到了 15T Tokens。从目前模型效果来看，Meta使用的Scaling Law法则是非常有效的，Meta得到了一个非常强大的模型，它非常小，易于使用和推理,而且mate表示，即使这样，该模型似乎也没有在标准意义上“收敛”,性能还能改善。这就意味着，一直以来我们使用的 LLM 训练是不足的，远远没有达到使模型收敛的那个点。较大的模型在训练计算较少的情况下可以与较小模型的性能相匹配，但考虑到推理过程中使效率更高，还是会选择小模型。如此说来训练和发布更多经过长期训练的甚至更小的模型，会不会是以后大模型发展的一个方向？
系统：为了训练最大的 Llama 3 模型，Meta结合了三种类型的并行化：数据并行化、模型并行化
和管道并行化。最高效的实现是在 16K GPU 上同时训练时，每个 GPU 的计算利用率超过 400 TFLOPS。在两个定制的 24K GPU 集群上进行了训练。
指令微调：为了在聊天用例中充分释放预训练模型的潜力，Meta对指令调整方法进行了创新。训练方法结合了监督微调 （SFT）、拒绝采样、近端策略优化（PPO） 和直接策略优化 （DPO） 的组合。这种组合训练，提高了模型在复杂推理任务中的表现。
模型效果：LLaMA 3有基础版，和 instruct两个版本。每个版本拥有 8B 和 70B 两种参数规模的模型，它们在多项行业基准测试中展示了最先进的性能，而且 instruct效果相当炸裂。

Grouped-Query Attention, GQA

多头注意力(Multi-Head Attention, MHA):
对于每一个注意力机制，qkv都需要存储h个头，为dim_q = hhead_dims, dim_k = hhead_dims, dim_v = hhead_dims 精度高，运算速度和显存占用大
多查询注意力(Multi-Query Attention, MQA)： 对于每一个注意力机制，q存储h个头，kv存储一个头，dim_q = hhead_dims, dim_k = 1head_dims, dim_v = 1head_dims 精度低一点，运算速度和显存占用小一点
分组查询注意力(Grouped-Query Attention, GQA)： 对于每一个注意力机制，q存储h个头，kv分成g组，kv存储个头，dim_q = hhead_dims, dim_k = ghead_dims, dim_v = g*head_dims MHA和MQA的折衷

数据清洗流程

数据清洗是指对数据进行审查和校验的过程，目的是删除重复信息、纠正存在的错误，并使数据保持一致性。其流程一般包括以下几个步骤：

数据收集

• 从各种数据源获取原始数据，这些数据源可能包括数据库、文件系统、网页、传感器等。数据的形式可以是结构化的（如表格数据）、半结构化的（如XML、JSON数据）或非结构化的（如文本、图像、音频等）。

数据集成

• 将从多个数据源收集到的数据结合起来并统一存储。在这个过程中，可能会遇到数据重复、数据不一致等问题，需要进行初步的处理和协调。

数据清理

• 去除重复数据：使用数据处理工具或编程语言中的相关函数，根据数据的唯一标识或特征来识别并删除重复的记录。
• 处理缺失值
  • 删除法：当缺失值的比例较低且对分析结果影响不大时，可以直接删除包含缺失值的记录。
  • 插补法：根据其他数据的特征和关系，使用均值、中位数、众数等统计量或基于机器学习算法来预测并填充缺失值。
• 纠正错误数据：通过数据验证和逻辑检查，发现并纠正数据中的错误。对于明显偏离正常范围的异常值，需要根据业务逻辑和数据特点进行处理，可能是修正为合理的值，也可能是删除。
• 数据标准化：将数据转换为统一的格式和标准，如日期格式、数字格式等，确保数据的一致性和可比性。对不同量纲和取值范围的特征进行标准化处理，使数据具有相同的尺度，常用的方法有Min-Max标准化、Z-Score标准化等。

数据转换

• 数据编码：将分类数据转换为数值形式，以便于模型处理，常见的编码方式有独热编码、标签编码等。
• 数据离散化：将连续型数据转换为离散型数据，例如将年龄划分为不同的年龄段。
• 特征提取与选择：从原始数据中提取出对分析和建模有意义的特征，并选择最具代表性和区分度的特征，去除冗余和无关的特征，降低数据维度，提高模型效率和准确性。

数据验证

• 数据质量评估：使用数据质量评估指标，如准确率、召回率、F1值、均方误差等，对清洗后的数据进行质量评估，检查数据是否满足业务需求和分析要求。
• 业务规则验证：根据具体的业务规则和逻辑，对数据进行再次检查，确保数据在业务层面的合理性和合规性。

数据存储

• 将清洗和处理后的数据存储到合适的数据仓库、数据库或文件系统中，以便后续的数据分析、挖掘和应用。

ppl 困惑度求法

四、机器学习知识点

1 LN和BN的原理与区别

BN的作用：

• 加快收敛
• 防止过拟合，防止朝着一个方向学习，会学到每个batch的特征
• 防止梯度爆炸和梯度消失
  
  
  

2、损失函数推导

手撕交叉熵损失代码

sigmoid公式和手撕代码

3 手撕多头注意力代码

Self-Attention

class MultiHeadAttention(nn.Module):
    def __init__(self):
        super(MultiHeadAttention, self).__init__()
        ## 输入进来的QKV是相等的，我们会使用映射linear做一个映射得到参数矩阵Wq, Wk,Wv
        self.W_Q = nn.Linear(d_model, d_k * n_heads)
        self.W_K = nn.Linear(d_model, d_k * n_heads)
        self.W_V = nn.Linear(d_model, d_v * n_heads)
        self.linear = nn.Linear(n_heads * d_v, d_model)
        self.layer_norm = nn.LayerNorm(d_model)
 
    def forward(self, Q, K, V, attn_mask):
 
        ## 这个多头分为这几个步骤，首先映射分头，然后计算atten_scores，然后计算atten_value;
        ##输入进来的数据形状： Q: [batch_size x len_q x d_model], K: [batch_size x len_k x d_model], V: [batch_size x len_k x d_model]
        residual, batch_size = Q, Q.size(0)
        # (B, S, D) -proj-> (B, S, D) -split-> (B, S, H, W) -trans-> (B, H, S, W)
 
        ##下面这个就是
 
 
 
 
        q_s = self.W_Q(Q).view(batch_size, -1, n_heads, d_k).transpose(1,2)  # q_s: [batch_size x n_heads x len_q x d_k]
        k_s = self.W_K(K).view(batch_size, -1, n_heads, d_k).transpose(1,2)  # k_s: [batch_size x n_heads x len_k x d_k]
        v_s = self.W_V(V).view(batch_size, -1, n_heads, d_v).transpose(1,2)  # v_s: [batch_size x n_heads x len_k x d_v]
 
        ## 输入进行的attn_mask形状是 batch_size x len_q x len_k，然后经过下面这个代码得到 新的attn_mask : [batch_size x n_heads x len_q x len_k]，就是把pad信息重复了n个头上
        attn_mask = attn_mask.unsqueeze(1).repeat(1, n_heads, 1, 1)
 
 
        ##然后我们计算 ScaledDotProductAttention 这个函数，去7.看一下
        ## 得到的结果有两个：context: [batch_size x n_heads x len_q x d_v], attn: [batch_size x n_heads x len_q x len_k]
        context, attn = ScaledDotProductAttention()(q_s, k_s, v_s, attn_mask)
        context = context.transpose(1, 2).contiguous().view(batch_size, -1, n_heads * d_v) # context: [batch_size x len_q x n_heads * d_v]
        output = self.linear(context)
        return self.layer_norm(output + residual), attn # output: [batch_size x len_q x d_model]

Cross-Attention

import torch
import torch.nn as nn

class CrossAttention(nn.Module):
    def __init__(self, d_in, d_out, dropout, num_heads, qkv_bias=False):
        super().__init__()
        assert d_out % num_heads == 0, "d_out 必须能够被 num_heads 整除"

        self.d_out = d_out
        self.num_heads = num_heads
        self.head_dim = d_out // num_heads  # 每个头的维度

        self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)  # 查询的线性变换
        self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)    # 键的线性变换
        self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)  # 值的线性变换
        self.out_proj = nn.Linear(d_out, d_out)               # 输出的线性变换
        self.dropout = nn.Dropout(dropout)                    # Dropout层

    def forward(self, queries, keys, values, mask=None):
        """
        queries: (batch_size, seq_len_q, d_in)
        keys: (batch_size, seq_len_kv, d_in)
        values: (batch_size, seq_len_kv, d_in)
        mask: (batch_size, num_heads, seq_len_q, seq_len_kv) 或 None
        """
        b, seq_len_q, d_in = queries.shape
        _, seq_len_kv, _ = keys.shape

        # 线性变换
        queries = self.W_query(queries)  # (b, seq_len_q, d_out)
        keys = self.W_key(keys)          # (b, seq_len_kv, d_out)
        values = self.W_value(values)    # (b, seq_len_kv, d_out)

        # 重塑为多头形式
        queries = queries.view(b, seq_len_q, self.num_heads, self.head_dim).transpose(1, 2)  # (b, num_heads, seq_len_q, head_dim)
        keys = keys.view(b, seq_len_kv, self.num_heads, self.head_dim).transpose(1, 2)      # (b, num_heads, seq_len_kv, head_dim)
        values = values.view(b, seq_len_kv, self.num_heads, self.head_dim).transpose(1, 2)  # (b, num_heads, seq_len_kv, head_dim)

        # 计算注意力得分
        attn_scores = torch.matmul(queries, keys.transpose(-2, -1))  # (b, num_heads, seq_len_q, seq_len_kv)
        attn_scores = attn_scores / (self.head_dim ** 0.5)            # 缩放

        # 应用mask（如果提供）
        if mask is not None:
            attn_scores = attn_scores.masked_fill(mask == 0, float('-inf'))

        # 计算注意力权重
        attn_weights = torch.softmax(attn_scores, dim=-1)            # (b, num_heads, seq_len_q, seq_len_kv)
        attn_weights = self.dropout(attn_weights)                   # Dropout

        # 计算上下文向量
        context_vec = torch.matmul(attn_weights, values)            # (b, num_heads, seq_len_q, head_dim)
        context_vec = context_vec.transpose(1, 2).contiguous()      # (b, seq_len_q, num_heads, head_dim)
        context_vec = context_vec.view(b, seq_len_q, self.d_out)    # (b, seq_len_q, d_out)

        # 输出投影
        context_vec = self.out_proj(context_vec)                    # (b, seq_len_q, d_out)

        return context_vec

# 设置随机种子以确保结果可复现
torch.manual_seed(123)

# 模拟查询和键值序列 (batch_size, seq_len_q/kv, d_in)
batch_size = 3
seq_len_q = 5  # 查询序列长度
seq_len_kv = 7  # 键和值的序列长度
d_in = 10      # 输入维度
d_out = 8      # 输出维度
num_heads = 2  # 多头数量
dropout = 0.1  # dropout 概率

# 创建 CrossAttention 实例
cross_attention = CrossAttention(d_in, d_out, dropout, num_heads)

# 输入的随机张量
queries = torch.randn(batch_size, seq_len_q, d_in)
keys = torch.randn(batch_size, seq_len_kv, d_in)
values = torch.randn(batch_size, seq_len_kv, d_in)

# 如果需要应用mask，例如因果遮蔽，可以创建mask
# 这里我们创建一个全1的mask，不进行遮蔽
mask = torch.ones(batch_size, num_heads, seq_len_q, seq_len_kv)

# 调用 forward 函数，输出上下文向量
output = cross_attention(queries, keys, values, mask=mask)

# 输出上下文向量的形状和内容
print("上下文向量的形状:", output.shape)
print("上下文向量 (context vectors):")
print(output)

3 为什么Relu能缓解梯度消失

ReLU（Rectified Linear Unit）函数能够在一定程度上解决梯度消失问题，主要与其函数特性及在反向传播中的梯度计算方式有关。下面为你详细阐述：

1. ReLU函数的定义

ReLU函数的数学表达式为：
$$f(x)=\{\begin{array}{ll}0,& \text{如果 }x<0\\ x,& \text{如果 }x\ge 0\end{array}$$

2. 梯度消失问题的背景

在深度神经网络中，梯度消失问题通常出现在采用Sigmoid或Tanh等激活函数的网络中。在反向传播过程中，梯度是从输出层向输入层逐层传递的。这些传统激活函数的导数在某些区间内的值较小，比如Sigmoid函数的导数$f^{\prime }(x)=f(x)(1-f(x))$，其值始终小于0.25 。当网络层数较多时，经过多层的梯度相乘，梯度会变得越来越小，最终趋近于0，导致靠近输入层的神经元的权重难以更新，网络训练难以收敛。

3. ReLU解决梯度消失的原理

• 正向传播：当输入$x\ge 0$时，ReLU函数的输出等于输入，这种线性关系使得信息能够较为直接地在网络中传递，避免了像Sigmoid等函数对信号的过度压缩。
• 反向传播：ReLU函数的导数为：
  $$f^{\prime }(x)=\{\begin{array}{ll}0,& \text{如果 }x<0\\ 1,& \text{如果 }x\ge 0\end{array}$$
  在反向传播过程中，当$x\ge 0$时，梯度在经过ReLU单元时不会发生衰减，因为其导数为1，这就保证了梯度能够有效地传递到前面的层，从而缓解了梯度消失的问题。即使在$x<0$时导数为0会导致神经元暂时不更新，但在实际训练中，部分神经元仍会处于$x\ge 0$的状态，使得网络整体仍能正常学习。

4. ReLU的改进：leakyReLU

1. Leaky ReLU函数定义

   • Leaky ReLU是ReLU函数的一种变体。其数学表达式为：
     $$f(x)=\{\begin{array}{ll}x,& \text{如果 }x\ge 0\\ \alpha x,& \text{如果 }x<0\end{array}$$
     其中，(\alpha)是一个较小的正数，通常取值在(0.01)左右。

2. 梯度消失问题背景回顾

   • 在深度神经网络训练中，梯度消失是一个常见问题。当使用如Sigmoid、Tanh等传统激活函数时，反向传播过程中梯度在各层间传递会不断衰减。例如，Sigmoid函数导数$f^{\prime }(x)=f(x)(1-f(x))$，其值最大为$0.25$。随着网络层数增加，经过多层的梯度相乘，梯度会趋近于(0)，使得靠近输入层的神经元权重更新缓慢，网络难以收敛。

3. Leaky ReLU解决梯度消失问题的原理

   • 正向传播：与ReLU类似，当$x\ge 0$时，Leaky ReLU输出为$x$，信号能直接传递。当$x<0$时，虽然函数值被压缩，但不像ReLU那样直接置零，而是乘以一个较小的非零系数$\alpha$，这使得负输入也能有一定程度的信号通过，避免了信息的完全丢失。
   • 反向传播：Leaky ReLU的导数为：
     $$f^{\prime }(x)=\{\begin{array}{ll}1,& \text{如果 }x\ge 0\\ \alpha ,& \text{如果 }x<0\end{array}$$
     在反向传播时，无论$x$的取值如何，梯度都不会为$0$。当$x\ge 0$时，梯度为$1$，不会导致梯度衰减；当$x<0$时，虽然梯度变为$\alpha$, $\alpha$较小但非零），相比于ReLU在$x<0$时梯度直接为$0$，Leaky ReLU能保证在整个定义域内都有梯度流动，使得处于负区间的神经元也能参与权重更新，从而在一定程度上解决了梯度消失问题，提升了深度神经网络的训练效果。

4 Adam优化器的原理

• 原点矩和中心矩：在概率论和统计学中，矩是用来描述随机变量的分布特征的一组数值。对于一个随机变量 $X$，其 $k$ 阶矩的定义如下：
• 原点矩：$E(X^k)$ ，表示随机变量 $X$ 的 $k$ 次方的期望。
• 中心矩：$E[(X-E(X){)}^k]$ ，其中 $E(X)$ 是随机变量 $X$ 的期望，它描述了随机变量相对于其均值的偏离程度。一阶原点矩就是随机变量的期望 $E(X)$ ，它反映了随机变量取值的平均水平；而一阶中心矩恒为 $0$ 。二阶原点矩 $E(X^2)$ 反映了随机变量平方的平均大小；二阶中心矩 $E[(X-E(X){)}^2]$ 就是方差，描述了随机变量相对于其均值的离散程度。

Adam（Adaptive Moment Estimation）优化器是一种常用于随机梯度下降的优化算法，广泛应用于深度学习模型训练。其原理综合了Adagrad和RMSProp算法的优点，能够自适应地调整每个参数的学习率。以下从核心概念、算法步骤、超参数等方面详细介绍Adam优化器原理：

1. 核心概念

• 梯度下降： 是一种常用的优化算法，旨在通过迭代更新模型参数，使目标函数值沿梯度相反方向下降，最终找到目标函数的最小值。在深度学习中，通过反向传播计算梯度，公式为$\theta =\theta -\alpha \nabla J(\theta )$，其中$\theta$是模型参数，$\alpha$是学习率，$\nabla J(\theta )$是目标函数$J(\theta )$关于参数$\theta$的梯度。
• 动量（Momentum）：模拟物理中的动量概念，在梯度下降过程中，不仅考虑当前梯度，还结合之前梯度的“惯性”。这有助于加速收敛，特别是在梯度方向一致的维度上，同时减少振荡，在梯度方向变化较大的维度上更稳定地更新。
• 自适应学习率：不同参数根据自身情况拥有独立学习率，在训练过程中动态调整。对于频繁更新的参数，降低学习率以避免步长过大导致错过最优解；对于更新不频繁的参数，增大学习率以促使其更快收敛。

2. 算法步骤

1. 初始化参数：
   • 初始化一阶矩估计（均值）$m_t$和二阶矩估计（未中心化的方差）$v_t$为0向量，即$m_0=0$，$v_0=0$。
   • 设置时间步$t=0$。
   • 选择超参数：学习率$\alpha$（通常为0.001），矩估计的指数衰减率${\beta }_1$（通常为0.9）和${\beta }_2$（通常为0.999），以及一个小常数$ϵ$（通常为$1e^{-8}$）防止除零操作。
2. 迭代更新：在每次迭代$t$中：
   • 计算梯度：给定当前参数${\theta }_t$，使用反向传播计算目标函数$J(\theta )$关于参数$\theta$的梯度$\nabla J({\theta }_t)$。
   • 更新一阶矩估计：计算梯度的指数加权移动平均（均值），公式为$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)\nabla J({\theta }_t)$。$m_t$近似为过去梯度的平均值，体现了当前梯度与过去梯度的综合影响。
   • 更新二阶矩估计：计算梯度平方的指数加权移动平均，公式为$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)(\nabla J({\theta }_t){)}^2$。$v_t$近似为过去梯度平方的平均值，反映了梯度的二阶矩信息，用于衡量梯度的变化幅度。
   • 偏差修正：由于$m_t$和$v_t$初始化为0，在训练初期会偏向于0，需要进行偏差修正。修正后的一阶矩估计为${\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}$，修正后的二阶矩估计为${\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}$。随着$t$增加，偏差修正的影响逐渐减小。
   • 更新参数：根据修正后的一阶矩和二阶矩估计更新参数，公式为${\theta }_{t+1}={\theta }_t-\frac{\alpha {\hat{m}}_t}{\sqrt{{\hat{v}}_t}+ϵ}$。这里$\frac{\alpha {\hat{m}}_t}{\sqrt{{\hat{v}}_t}+ϵ}$相当于调整后的学习率，它根据每个参数的梯度统计信息自适应变化。

3. 超参数说明

• 学习率$\alpha$：决定参数更新步长，过大可能导致错过最优解，过小则使收敛速度过慢。
• 矩估计的指数衰减率${\beta }_1$和${\beta }_2$：${\beta }_1$控制一阶矩估计中过去梯度信息的保留程度，接近1时，$m_t$对历史梯度记忆更久；${\beta }_2$控制二阶矩估计中过去梯度平方信息的保留程度，接近1时，$v_t$对历史梯度平方记忆更久。
• $ϵ$：防止分母为零，保证算法稳定性，通常设为一个极小正数。

Adam优化器虽然主要是基于数学推导与算法设计，但其中部分机制可以类比一些物理原理，这有助于直观理解其工作方式：

1. 动量（Momentum）类比

• 物理动量原理：在物理学中，动量是与物体的质量和速度相关的物理量，其定义为 (p = mv)（(p) 是动量，(m) 是质量，(v) 是速度）。一个具有动量的物体在不受外力作用时，会保持匀速直线运动状态。当受到外力作用时，外力会改变物体的动量，进而改变其速度。
• Adam优化器中的类比：在Adam优化器中，一阶矩估计 (m_t) 类似于动量的概念。公式 (m_t = \beta_1 m_{t - 1} + (1 - \beta_1)\nabla J(\theta_t)) 可以类比为物体动量的更新。这里 ((1 - \beta_1)\nabla J(\theta_t)) 类似于施加在物体上的外力（梯度类似于力的方向和大小），它改变了动量 (m_t) 的大小和方向。而 (\beta_1 m_{t - 1}) 则像是物体由于惯性保持原来的运动趋势。通过这种方式，优化过程不仅仅依赖于当前的梯度（力），还考虑了过去梯度的累积影响，使得参数更新能够在一定程度上保持方向的一致性，避免在复杂的损失函数空间中频繁改变方向，就像具有动量的物体不会轻易突然转向一样，有助于加速收敛。

2. 自适应学习率与摩擦力类比

• 摩擦力原理：摩擦力是阻碍物体相对运动或相对运动趋势的力。当一个物体在不同表面上运动时，不同表面的摩擦系数不同，会导致物体受到不同大小的摩擦力，从而影响物体的运动速度。例如，在粗糙表面上摩擦力大，物体运动速度会较快降低；在光滑表面上摩擦力小，物体能保持相对较高的速度运动。
• Adam优化器中的类比：Adam优化器中的二阶矩估计 (v_t) 以及基于它得到的自适应学习率部分与摩擦力概念有相似之处。二阶矩估计 (v_t = \beta_2 v_{t - 1} + (1 - \beta_2)(\nabla J(\theta_t))^2) 反映了梯度变化的幅度。在更新参数的公式 (\theta_{t + 1} = \theta_t - \frac{\alpha \hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}) 中，(\sqrt{\hat{v}_t}) 类似于一种“摩擦力”，它会根据梯度的波动情况自适应地调整参数更新的步长。如果梯度波动较大（即 (\sqrt{\hat{v}_t}) 较大），相当于“摩擦力”较大，那么参数更新的步长就会变小，就像物体在粗糙表面上运动速度减慢一样，避免参数更新过于激进；反之，如果梯度波动较小（(\sqrt{\hat{v}_t}) 较小），则步长相对较大，如同物体在光滑表面上能更顺畅地移动。这样，自适应学习率机制能够根据每个参数的梯度变化情况，动态地调整更新步长，使优化过程更加稳定和高效。

总之，给物体一个外力并不会直接将动量变成这个力的，而是产生的动量影响被叠加到原来的动量上，使得梯度的变化趋势变缓，而二阶矩估计再开方可以衡量梯度变化的大小趋势，而使用动量可以使其变化大小得到缓和。

5 AUC曲线计算

真正例（True Positive，TP）、假反例（False Negative，FN）、假正例（False Positive，FP）和真反例（True Negative，TN）是在二分类问题中用于评估模型预测结果的重要概念，以下结合具体例子进行详细定义：

基本定义

在二分类问题里，样本的真实标签只有两种类别，通常标记为正类（Positive）和负类（Negative）；而模型对样本的预测结果同样也分为正类和负类。通过将真实标签和预测结果进行交叉对比，就能得到这四个评估指标。

真实情况 \ 预测结果	预测为正类	预测为负类
实际为正类	真正例（TP）	假反例（FN）
实际为负类	假正例（FP）	真反例（TN）

这个给后面的

详细解释

• 真正例（TP）：指的是那些实际属于正类，并且被模型正确地预测为正类的样本。例如在一个癌症诊断的二分类问题中，正类代表患有癌症，负类代表未患癌症。如果一个患者实际上患有癌症，而模型也准确地预测该患者患有癌症，那么这个样本就属于真正例。
• 假反例（FN）：表示实际属于正类，但模型却错误地预测为负类的样本。继续以癌症诊断为例，若一个患者实际上患有癌症，但模型却预测该患者未患癌症，这个样本就属于假反例，也被称为漏诊。
• 假正例（FP）：是指实际属于负类，然而模型却错误地预测为正类的样本。在癌症诊断场景中，如果一个患者实际上并未患癌症，但模型却预测该患者患有癌症，这个样本就属于假正例，也被称为误诊。
• 真反例（TN）：即实际属于负类，同时模型也正确地预测为负类的样本。在癌症诊断中，若一个患者实际上未患癌症，模型也准确地预测该患者未患癌症，那么这个样本就属于真反例。
  正例和反例都是根据模型的预测结果来说的，预测的是正就是正样例，预测的是反就是负样例。

基本概念

ROC曲线以假正率（False Positive Rate，FPR）为横轴，真正率（True Positive Rate，TPR）为纵轴，通过在不同分类阈值下计算FPR和TPR的值，将这些值对应的点连接起来形成的曲线。在二分类问题中，模型会对每个样本预测一个属于正类的概率，通过设定不同的阈值，可以将样本划分为正类或负类，不同的阈值会导致不同的FPR和TPR组合，从而在ROC曲线上表现为不同的点。

相关指标计算

• 真正率（TPR）：也称为灵敏度（Sensitivity）或召回率（Recall），表示模型正确预测为正类的样本占实际正类样本的比例。计算公式为$TPR=\frac{TP}{TP+FN}$，其中$TP$（True Positive）是真正例，即实际为正类且被模型正确预测为正类的样本数量；$FN$（False Negative）是假反例，即实际为正类但被模型错误预测为负类的样本数量。
• 假正率（FPR）：表示模型错误预测为正类的样本占实际负类样本的比例。计算公式为$FPR=\frac{FP}{FP+TN}$，其中$FP$（False Positive）是假正例，即实际为负类但被模型错误预测为正类的样本数量；$TN$（True Negative）是真反例，即实际为负类且被模型正确预测为负类的样本数量。
  真正率是所有正样本中被模型预测为正的比例，假正率是所有负样本中被模型预测为正确的比例

绘制方法

1. 预测概率：使用训练好的二分类模型对测试集样本进行预测，得到每个样本属于正类的概率。
2. 设定阈值：从预测概率的最大值到最小值之间选择一系列不同的阈值。
3. 计算指标：对于每个阈值，根据上述公式计算对应的TPR和FPR。
4. 绘制曲线：以FPR为横轴，TPR为纵轴，将每个阈值下计算得到的(FPR, TPR)点绘制在平面直角坐标系中，然后将这些点连接起来，就得到了ROC曲线。

ROC曲线的特点和解读

• 对角线：ROC曲线中的对角线（从点(0, 0)到点(1, 1)的直线）表示一个随机分类器的性能。也就是说，如果一个模型的ROC曲线接近这条对角线，说明该模型的分类效果与随机猜测差不多。
• 曲线位置：ROC曲线越靠近左上角，说明模型的性能越好。因为左上角对应的点是(0, 1)，即FPR为0且TPR为1，这意味着模型能够完美地将正类和负类样本区分开来。
• AUC值：ROC曲线下的面积（Area Under the Curve，AUC）是一个常用的衡量模型性能的指标。AUC的取值范围在0到1之间，AUC值越大，说明模型的性能越好。当AUC = 0.5时，模型性能等同于随机分类器；当AUC = 1时，模型具有完美的分类性能。
• 你想问的可能是AUC（Area Under the Curve），它指的是ROC曲线（受试者工作特征曲线）下的面积，是衡量二分类模型性能的重要指标。以下为你详细介绍其计算方式：

1. 基于定义的积分计算（理论方法）

从数学定义上讲，AUC是ROC曲线下的面积。由于ROC曲线是连续的，但在实际计算中我们只有有限个样本，因此通常采用离散化的方法近似计算该积分。

2. 基于排序的方法

原理

AUC可以理解为在所有正负样本对中，正样本预测概率大于负样本预测概率的概率。

计算步骤

设正样本数量为$m$，负样本数量为$n$。

• 将所有样本（正样本和负样本）按照模型预测为正类的概率进行降序排列。
• 遍历排序后的样本，对于每个正样本，统计排在它后面的负样本的数量，将这些数量累加起来，记为$sum$。
• 根据公式$AUC=\frac{sum}{m\times n}$计算AUC值。

Python代码示例

import numpy as np

def auc_calculate(y_true, y_scores):
    pos_scores = y_scores[y_true == 1]
    neg_scores = y_scores[y_true == 0]
    m = len(pos_scores)
    n = len(neg_scores)
    sum_rank = 0
    for pos in pos_scores:
        for neg in neg_scores:
            if pos > neg:
                sum_rank += 1
            elif pos == neg:
                sum_rank += 0.5
    auc = sum_rank / (m * n)
    return auc

# 示例数据
y_true = np.array([1, 1, 0, 0])
y_scores = np.array([0.8, 0.7, 0.3, 0.2])
print(auc_calculate(y_true, y_scores))

3. 基于ROC曲线离散点的梯形面积求和法

原理

通过在不同分类阈值下计算FPR（假正率）和TPR（真正率），得到一系列坐标点，连接这些点形成ROC曲线，然后计算这些离散点构成的梯形面积之和来近似ROC曲线下的面积。

计算步骤

• 确定不同阈值下的TPR和FPR：从预测概率的最大值到最小值之间选择一系列的阈值$t$。对于每个阈值$t$，统计预测概率大于等于$t$的正样本数量（真正例，$TP$）、负样本数量（假正例，$FP$），以及实际正样本总数（$P$）和实际负样本总数（$N$）。根据公式$TPR=\frac{TP}{P}$，$FPR=\frac{FP}{N}$分别计算真正率和假正率。
• 计算AUC：将得到的所有点按照FPR从小到大排序。假设共有$k$个点$(FP{R}_i,TP{R}_i)$，$i=1,2,\cdots ,k$，且$FP{R}_1=0$，$TP{R}_1=0$，$FP{R}_k=1$，$TP{R}_k=1$。AUC通过对相邻点之间的梯形面积进行累加得到，公式为$AUC={\sum }_{i=1}^{k-1}\frac{(FP{R}_{i+1}-FP{R}_i)\times (TP{R}_{i+1}+TP{R}_i)}{2}$。

Python代码示例

from sklearn.metrics import roc_curve, auc
import numpy as np

y_true = np.array([1, 1, 0, 0])
y_scores = np.array([0.8, 0.7, 0.3, 0.2])
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
auc_value = auc(fpr, tpr)
print(auc_value)

4. 使用专门的机器学习库计算

许多机器学习库都提供了直接计算AUC的函数，如scikit-learn库中的roc_auc_score函数。

Python代码示例

from sklearn.metrics import roc_auc_score
import numpy as np

y_true = np.array([1, 1, 0, 0])
y_scores = np.array([0.8, 0.7, 0.3, 0.2])
auc_value = roc_auc_score(y_true, y_scores)
print(auc_value)

这些方法各有优缺点，基于排序的方法直观易懂，但在样本数量较大时计算效率较低；基于梯形面积求和的方法和使用库函数的方法计算效率较高，在实际应用中更为常用。

6 python装饰器的作用

Python装饰器是一种特殊的函数，它可以接受一个函数作为输入，并返回一个新的函数。装饰器本质上是一个语法糖，用于增强函数或类的功能，而无需修改它们的源代码。以下详细介绍装饰器的常见作用：

1. 代码复用与功能增强

装饰器可以将一些通用的功能封装起来，然后应用到多个函数上，避免代码重复。比如，日志记录、性能测试、权限验证等功能，都可以通过装饰器来实现。

日志记录示例

def log_decorator(func):
    def wrapper(*args, **kwargs):
        print(f"Calling function {func.__name__} with args: {args}, kwargs: {kwargs}")
        result = func(*args, **kwargs)
        print(f"Function {func.__name__} finished execution.")
        return result
    return wrapper

@log_decorator
def add(a, b):
    return a + b

print(add(3, 5))

在这个例子中，log_decorator 是一个装饰器，它在调用被装饰的函数前后添加了日志记录功能。通过 @log_decorator 语法，将这个功能应用到了 add 函数上。

2. 性能测试

使用装饰器可以方便地对函数的执行时间进行测量，帮助开发者找出性能瓶颈。

性能测试示例

import time

def performance_decorator(func):
    def wrapper(*args, **kwargs):
        start_time = time.time()
        result = func(*args, **kwargs)
        end_time = time.time()
        print(f"Function {func.__name__} took {end_time - start_time} seconds to execute.")
        return result
    return wrapper

@performance_decorator
def long_running_function():
    time.sleep(2)
    return "Done"

print(long_running_function())

这个例子中，performance_decorator 装饰器记录了 long_running_function 函数的执行时间。

3. 权限验证

在Web开发或其他需要权限控制的场景中，可以使用装饰器来验证用户是否具有执行某个函数的权限。

权限验证示例

def auth_decorator(func):
    def wrapper(user, *args, **kwargs):
        if user == "admin":
            return func(user, *args, **kwargs)
        else:
            print("You don't have permission to execute this function.")
    return wrapper

@auth_decorator
def sensitive_operation(user):
    print("Performing sensitive operation...")

sensitive_operation("admin")
sensitive_operation("guest")

这里的 auth_decorator 装饰器会检查用户是否为 “admin”，如果是则允许执行被装饰的函数，否则给出权限不足的提示。

4. 缓存功能

装饰器可以实现函数结果的缓存，避免重复计算，提高程序的运行效率。

缓存示例

def cache_decorator(func):
    cache = {}
    def wrapper(*args):
        if args in cache:
            return cache[args]
        result = func(*args)
        cache[args] = result
        return result
    return wrapper

@cache_decorator
def factorial(n):
    if n == 0 or n == 1:
        return 1
    return n * factorial(n - 1)

print(factorial(5))
print(factorial(5))  # 第二次调用直接从缓存中获取结果

在这个例子中，cache_decorator 装饰器使用一个字典来缓存函数的计算结果，当再次调用相同参数的函数时，直接从缓存中返回结果，避免了重复计算。

5. 代码解耦

装饰器可以将与核心业务逻辑无关的功能（如日志、权限验证等）从函数中分离出来，使代码结构更加清晰，提高代码的可维护性和可测试性。被装饰的函数只需要专注于实现核心业务逻辑，而其他辅助功能由装饰器来完成。

7 softmax的公式和代码实现

1. Softmax公式

Softmax函数常用于多分类问题中，它将一个实数向量转换为一个概率分布，使得向量中的每个元素都在0到1之间，并且所有元素的和为1。

假设输入向量为 $\mathbf{z}=[z_1,z_2,\cdots ,z_K]$，其中 $K$ 是向量的维度，Softmax函数对向量 $\mathbf{z}$ 中的第 $i$ 个元素的计算方式如下：

$$\sigma (\mathbf{z}{)}_i=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}\text{for }i=1,2,\cdots ,K$$

其中，$\sigma (\mathbf{z}{)}_i$ 表示经过Softmax变换后向量的第 $i$ 个元素，$e$ 是自然常数（约为2.71828）。

2. 代码实现

2.1 使用Python原生代码实现

import math

def softmax(z):
    """
    实现softmax函数
    :param z: 输入的实数列表
    :return: 经过softmax变换后的概率分布列表
    """
    exp_values = [math.exp(i) for i in z]
    sum_exp = sum(exp_values)
    return [i / sum_exp for i in exp_values]

# 示例输入
z = [1.0, 2.0, 3.0]
result = softmax(z)
print(result)

2.2 使用NumPy库实现

import numpy as np

def softmax_numpy(z):
    """
    使用NumPy实现softmax函数
    :param z: 输入的NumPy数组
    :return: 经过softmax变换后的概率分布NumPy数组
    """
    exp_values = np.exp(z)
    sum_exp = np.sum(exp_values)
    return exp_values / sum_exp

# 示例输入
z = np.array([1.0, 2.0, 3.0])
result = softmax_numpy(z)
print(result)

2.3 处理数值稳定性问题

在实际应用中，当输入的元素值较大时，直接使用上述公式可能会导致数值溢出问题。为了解决这个问题，可以通过减去输入向量中的最大值来进行数值稳定化处理。

import numpy as np

def stable_softmax(z):
    """
    实现数值稳定的softmax函数
    :param z: 输入的NumPy数组
    :return: 经过softmax变换后的概率分布NumPy数组
    """
    z = z - np.max(z)  # 减去最大值以避免数值溢出
    exp_values = np.exp(z)
    sum_exp = np.sum(exp_values)
    return exp_values / sum_exp

# 示例输入
z = np.array([1000.0, 1001.0, 1002.0])
result = stable_softmax(z)
print(result)

在深度学习框架中，如TensorFlow和PyTorch，也提供了内置的Softmax函数，使用起来更加方便，例如在PyTorch中可以这样使用：

import torch
import torch.nn.functional as F

z = torch.tensor([1.0, 2.0, 3.0])
result = F.softmax(z, dim=0)
print(result)

这些实现方式都基于Softmax的基本公式，通过不同的工具和方法完成了将输入向量转换为概率分布的功能。

在Softmax函数中使用指数运算而非直接求比例，主要有以下几个方面的原因：

1. 突出差异

• 放大输入值的差异：指数函数是一个单调递增的函数，并且增长速度非常快。当输入向量中的元素存在差异时，经过指数运算后，这些差异会被显著放大。例如，假设有两个输入值 $z_1=1$ 和 $z_2=3$，直接求比例可能不能很好地体现出它们之间的相对大小关系。但如果使用指数运算，$e^1\approx 2.72$，$e^3\approx 20.09$，差异被明显放大。
• 增强区分度：在多分类问题中，这种放大差异的特性非常有用。它可以使得模型更倾向于选择概率最大的类别，增强了分类结果的区分度。例如在图像分类任务中，模型对不同类别的预测得分经过Softmax处理后，得分较高的类别对应的概率会远远大于得分较低的类别，从而更明确地给出分类结果。

2. 保证输出为正

• 指数函数的非负性：指数函数 $y=e^x$ 的值域始终大于 0，对于任意实数 $x$，$e^x>0$。这确保了Softmax函数的输出，即每个类别的概率都是非负的，符合概率的基本定义（概率值必须在 0 到 1 之间）。
• 避免负概率问题：如果直接求比例，输入值可能为负数，会导致计算出的比例也可能为负数，这在概率的概念中是没有意义的。而使用指数运算可以避免这个问题，保证所有输出都是有效的概率值。

3. 可微性

• 便于梯度计算：在深度学习中，模型的训练通常基于梯度下降等优化算法，这就要求目标函数是可微的。指数函数具有良好的可微性，其导数形式简单（$ (e^x)\prime=e^x$）。Softmax函数使用指数运算后，在计算梯度时相对容易，使得模型可以通过反向传播算法高效地更新参数。
• 支持模型优化：可微性是模型能够进行有效训练的关键。如果不使用指数运算而直接求比例，可能会导致函数不可微或者求导过程非常复杂，从而影响模型的训练效率和性能。

4. 数学性质良好

• 满足概率分布要求：Softmax函数通过指数运算和归一化处理，使得输出的向量满足概率分布的两个基本条件：所有元素非负且元素之和为 1。这使得它可以很好地应用于多分类问题中，将模型的输出转化为每个类别的概率估计。

8 如何缓解梯度爆炸和梯度消失

梯度爆炸和梯度消失是在深度神经网络训练过程中常见的问题，会导致模型无法有效学习。以下分别介绍这两个问题产生的原因及对应的缓解方法。

梯度爆炸

原因

在深度神经网络中，梯度是通过反向传播算法计算得到的。当网络层数较多时，梯度在反向传播过程中可能会不断累积，导致梯度的范数变得非常大，从而引发梯度爆炸。这通常发生在使用Sigmoid或Tanh等激活函数，以及学习率设置过大的情况下。

缓解方法

• 梯度裁剪（Gradient Clipping）
  • 原理：在反向传播计算得到梯度后，对梯度的范数进行限制。如果梯度的范数超过了预设的阈值，就将梯度按比例缩小，使得梯度的范数不超过该阈值。
  • 代码示例（使用PyTorch）：

import torch
import torch.nn as nn
import torch.optim as optim

model = nn.Sequential(
    nn.Linear(10, 20),
    nn.ReLU(),
    nn.Linear(20, 1)
)
optimizer = optim.SGD(model.parameters(), lr=0.01)
loss_fn = nn.MSELoss()

# 模拟训练过程
inputs = torch.randn(32, 10)
targets = torch.randn(32, 1)

optimizer.zero_grad()
outputs = model(inputs)
loss = loss_fn(outputs, targets)
loss.backward()

# 梯度裁剪
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)

optimizer.step()

• 使用合适的优化器
  • 原理：一些优化器（如Adagrad、Adadelta、RMSProp和Adam）能够自适应地调整每个参数的学习率，从而在一定程度上缓解梯度爆炸的问题。这些优化器会根据梯度的历史信息动态地调整学习率，避免某些参数的梯度过大。

梯度消失

原因

梯度消失通常是由于使用了Sigmoid或Tanh等激活函数，这些函数在输入值较大或较小时，导数趋近于 0。在深度神经网络中，梯度在反向传播过程中需要不断乘以激活函数的导数，当网络层数较多时，多次乘以趋近于 0 的导数会导致梯度变得非常小，甚至趋近于 0，从而使得模型无法有效地更新参数。

缓解方法

• 使用合适的激活函数

  • ReLU及其变体：ReLU（Rectified Linear Unit）激活函数的定义为 $f(x)=\max (0,x)$，其导数在 $x>0$ 时为 1，在 $x\le 0$ 时为 0。ReLU能够有效地缓解梯度消失问题，因为它在正区间内的导数为常数 1，不会使梯度在反向传播过程中不断变小。此外，还有一些ReLU的变体，如Leaky ReLU、Parametric ReLU等，它们在 $x\le 0$ 时也有一个非零的导数，进一步避免了“神经元死亡”的问题。

• 批量归一化（Batch Normalization）

  • 原理：批量归一化是在神经网络的每一层输入之前，对输入数据进行归一化处理，使得输入数据的均值为 0，方差为 1。这样可以加速网络的收敛速度，缓解梯度消失问题。批量归一化还具有一定的正则化作用，能够提高模型的泛化能力。

• 残差连接（Residual Connection）

  • 原理：残差连接是在深度神经网络中引入的一种结构，它允许网络跳过一些层，直接将输入连接到后面的层。这样可以使得梯度在反向传播过程中能够更直接地传递，避免了梯度在多层之间传递时不断衰减。

9 KL散度

KL散度（Kullback - Leibler Divergence）的推导可以从信息论的角度出发，下面将详细介绍其推导过程，分为离散概率分布和连续概率分布两种情况。

离散概率分布下KL散度的推导

1. 信息熵

在信息论中，信息熵（Entropy）是用来衡量一个随机变量不确定性的指标。对于一个离散随机变量 $X$，其取值为 $x_1,x_2,\cdots ,x_n$，对应的概率分布为 $P(X=x_i)=p_i$，其中 ${\sum }_{i=1}^n{p}_i=1$ 且 $p_i\ge 0$，则 $X$ 的信息熵 $H(P)$ 定义为：
$$H(P)=-\sum _{i=1}^n{p}_i\log p_i$$
信息熵越大，说明随机变量的不确定性越大。

2. 交叉熵

假设我们有另一个概率分布 $Q$，其取值为 $x_1,x_2,\cdots ,x_n$，对应的概率为 $q_i$，其中 ${\sum }_{i=1}^n{q}_i=1$ 且 $q_i\ge 0$。交叉熵 $H(P,Q)$ 用于衡量使用概率分布 $Q$ 来编码服从概率分布 $P$ 的数据时所需要的平均编码长度，定义为：
[H(P,Q)=-\sum_{i = 1}^{n}p_i\log q_i]

3. KL散度的推导

KL散度可以理解为使用概率分布 $Q$ 来近似概率分布 $P$ 时所增加的平均编码长度，即交叉熵与信息熵的差值。
$$\begin{array}{rl}{D}_{KL}(P||Q)& =H(P,Q)-H(P)\\ & =-\sum _{i=1}^n{p}_i\log q_i-(-\sum _{i=1}^n{p}_i\log p_i)\\ & =\sum _{i=1}^n{p}_i\log p_i-\sum _{i=1}^n{p}_i\log q_i\\ & =\sum _{i=1}^n{p}_i(\log p_i-\log q_i)\\ & =\sum _{i=1}^n{p}_i\log \frac{p_i}{q_i}\end{array}$$

连续概率分布下KL散度的推导

1. 连续随机变量的信息熵

对于连续随机变量 $X$，其概率密度函数为 $p(x)$，则 $X$ 的信息熵 $H(P)$ 定义为：
[H§=-\int_{-\infty}^{\infty}p(x)\log p(x)dx]

2. 连续随机变量的交叉熵

假设有另一个概率密度函数 $q(x)$，则使用 $q(x)$ 来编码服从 $p(x)$ 的数据时的交叉熵 $H(P,Q)$ 定义为：
[H(P,Q)=-\int_{-\infty}^{\infty}p(x)\log q(x)dx]

3. KL散度的推导

同样，KL散度是交叉熵与信息熵的差值：
$$\begin{array}{rl}{D}_{KL}(P||Q)& =H(P,Q)-H(P)\\ & =-{\int }_{-\infty }^{\infty }p(x)\log q(x)dx-(-{\int }_{-\infty }^{\infty }p(x)\log p(x)dx)\\ & ={\int }_{-\infty }^{\infty }p(x)\log p(x)dx-{\int }_{-\infty }^{\infty }p(x)\log q(x)dx\\ & ={\int }_{-\infty }^{\infty }p(x)(\log p(x)-\log q(x))dx\\ & ={\int }_{-\infty }^{\infty }p(x)\log \frac{p(x)}{q(x)}dx\end{array}$$

综上所述，通过信息熵和交叉熵的概念，我们可以推导出离散概率分布和连续概率分布下的KL散度公式。KL散度衡量了用一个概率分布去近似另一个概率分布时所损失的信息。
KL散度（Kullback - Leibler Divergence），也被称为相对熵，是用于衡量两个概率分布之间差异的一种度量方法。下面从定义、公式、性质和应用场景几个方面详细介绍：

定义与直观理解

KL散度可以理解为描述当用一个概率分布 $Q$ 来近似另一个概率分布 $P$ 时所损失的信息。如果两个概率分布完全相同，那么KL散度的值为 0；两个分布之间的差异越大，KL散度的值也就越大。

公式

• 离散概率分布：
  假设 $P(x)$ 和 $Q(x)$ 是定义在离散随机变量 $X$ 上的两个概率分布，那么 $P$ 相对于 $Q$ 的KL散度定义为：
  [D_{KL}(P||Q)=\sum_{x\in\mathcal{X}}P(x)\log\frac{P(x)}{Q(x)}]
  其中，$\mathcal{X}$ 是随机变量 $X$ 的取值空间，$\log$ 通常是以自然常数 $e$ 为底。
• 连续概率分布：
  若 $P(x)$ 和 $Q(x)$ 是连续随机变量 $X$ 的概率密度函数，那么 $P$ 相对于 $Q$ 的KL散度定义为：
  [D_{KL}(P||Q)=\int_{-\infty}^{\infty}P(x)\log\frac{P(x)}{Q(x)}dx]

性质

• 非负性：$D_{KL}(P||Q)\ge 0$，当且仅当 $P(x)=Q(x)$ 对于所有的 $x$ 都成立时，等号成立。这表明用一个分布去近似另一个分布时，总会有信息损失，除非两个分布完全相同。
• 不对称性：一般情况下，$D_{KL}(P||Q)\ne D_{KL}(Q||P)$。这意味着KL散度不是一个真正意义上的距离度量（距离度量需要满足对称性），它只是一种衡量两个分布差异的指标。

应用场景

• 机器学习
  • 模型训练：在很多机器学习算法中，如变分自编码器（VAE），KL散度被用于衡量模型学习到的分布与目标分布之间的差异，作为损失函数的一部分来优化模型参数，使得模型生成的样本分布尽可能接近真实数据的分布。
  • 特征选择：可以通过计算不同特征对应的概率分布与目标变量分布之间的KL散度，来评估特征的重要性，从而选择出对模型预测最有帮助的特征。
• 信息论：在信息论中，KL散度用于衡量两个信源之间的差异。例如，在数据压缩中，可以通过最小化KL散度来找到最优的编码方案，使得编码后的信息损失最小。
• 统计学：在统计学中，KL散度可以用于比较两个统计模型的拟合优度。通过计算观测数据的经验分布与模型预测分布之间的KL散度，可以评估模型对数据的拟合程度。

在上述代码中，使用 scipy.special.rel_entr 函数计算两个离散概率分布之间的相对熵，然后求和得到KL散度。

10 手撕NMS

优化前

import numpy as np

def nms(dets, iou_thred, cfd_thred):
    if len(dets)==0: return []
    bboxes = np.array(dets)
    ## 对整个bboxes排序
    bboxes = bboxes[np.argsort(bboxes[:,4])]
    pick_bboxes = []
#     print(bboxes)
    while bboxes.shape[0] and bboxes[-1,-1] >= cfd_thred:
        bbox = bboxes[-1]
        x1 = np.maximum(bbox[0], bboxes[:-1,0])
        y1 = np.maximum(bbox[1], bboxes[:-1,1])
        x2 = np.minimum(bbox[2], bboxes[:-1,2])
        y2 = np.minimum(bbox[3], bboxes[:-1,3])
        inters = np.maximum(x2-x1+1, 0) * np.maximum(y2-y1+1, 0)
        unions = (bbox[2]-bbox[0]+1)*(bbox[3]-bbox[1]+1) + (bboxes[:-1,2]-bboxes[:-1,0]+1)*(bboxes[:-1,3]-bboxes[:-1,1]+1) - inters
        ious = inters/unions
        keep_indices = np.where(ious<iou_thred)
        bboxes = bboxes[keep_indices]	## indices一定不包括自己
        pick_bboxes.append(bbox)
    return np.asarray(pick_bboxes)
    


###   肌肉记忆了
import numpy as np

def nms(preds, iou_thred=0.5, score_thred=0.5):
    ## preds: N * 5, [x1, y1, x2, y2, score]
    orders = np.argsort(preds[:,4])
    det = []
    arears = (preds[:, 2] - preds[:, 0]) * (preds[:, 3] - preds[:, 1])
    while orders.shape[0] and preds[orders[-1], 4] >= score_thred:
        pick = preds[orders[-1]]
        xx1 = np.maximum(pick[0], preds[orders[:-1], 0])
        yy1 = np.maximum(pick[1], preds[orders[:-1], 1])
        xx2 = np.minimum(pick[2], preds[orders[:-1], 2])
        yy2 = np.minimum(pick[3], preds[orders[:-1], 3])
        inters = np.maximum((xx2-xx1), 0) * np.maximum((yy2-yy1), 0)
        unions = arears[orders[-1]] + arears[orders[:-1]] - inters
        iou = inters / unions
        keep = iou < iou_thred
        orders = orders[:-1][keep]
        det.append(pick)
    return np.asarray(det)
    
dets = np.asarray([[187, 82, 337, 317, 0.9], [150, 67, 305, 282, 0.75], [246, 121, 368, 304, 0.8]])
nms(dets)
dets = [[187, 82, 337
, 317, 0.9], [150, 67, 305, 282, 0.75], [246, 121, 368, 304, 0.8]]
dets_nms =  nms(dets, 0.5, 0.3)
print(dets_nms)

优化后

import numpy as np

def nms(dets, iou_thred, cfd_thred):
    if len(dets)==0: return []
    bboxes = np.array(dets)
    ## 维护orders
    orders = np.argsort(bboxes[:,4])
    pick_bboxes = []
    x1 = bboxes[:,0]
    y1 = bboxes[:,1]
    x2 = bboxes[:,2]
    y2 = bboxes[:,3]
    areas = (x2-x1+1)*(y2-y1+1)		## 提前计算好bboxes面积，防止在循环中重复计算
    
    while orders.shape[0] and bboxes[orders[-1],-1] >= cfd_thred:
        bbox = bboxes[orders[-1]]
        xx1 = np.maximum(bbox[0], x1[orders[:-1]])
        yy1 = np.maximum(bbox[1], y1[orders[:-1]])
        xx2 = np.minimum(bbox[2], x2[orders[:-1]])
        yy2 = np.minimum(bbox[3], y2[orders[:-1]])
        inters = np.maximum(xx2-xx1+1, 0) * np.maximum(yy2-yy1+1, 0)
        unions = areas[orders[-1]] + areas[orders[:-1]] - inters
        ious = inters/unions
        keep_indices = np.where(ious<iou_thred)
        pick_bboxes.append(bbox)
        orders = orders[keep_indices]
    return np.asarray(pick_bboxes)
    

dets = [[187, 82, 337, 317, 0.9], [150, 67, 305, 282, 0.75], [246, 121, 368, 304, 0.8]]
dets_nms = nms(dets, 0.5, 0.3)
print(dets_nms)

11 L1正则化和L2正则化的区别

L1和L2正则化是机器学习和深度学习中常用的正则化方法，它们都用于防止模型过拟合，提高模型的泛化能力，但在原理、数学形式、对模型参数的影响以及应用场景等方面存在一些区别

数学形式

• L1正则化：也称为Lasso正则化，它是在原目标函数（损失函数）的基础上加上参数的绝对值之和作为正则化项。对于线性回归模型，假设原目标函数为均方误差 $J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$，加入L1正则化后的目标函数为：
  $J_{L1}(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\frac{\lambda }{m}{\sum }_{j=1}^n|{\theta }_j|$
  其中，$\lambda$ 是正则化参数，控制正则化的强度，${\theta }_j$ 是模型的参数，$m$ 是样本数量，$n$ 是参数的数量。
• L2正则化：也称为Ridge正则化，它是在原目标函数的基础上加上参数的平方和作为正则化项。同样对于线性回归模型，加入L2正则化后的目标函数为：
  $J_{L2}(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$

对模型参数的影响

• 参数稀疏性
  • L1正则化：具有产生稀疏解的特性，即它会使部分参数变为零。这是因为L1正则化的导数在参数为零时不可导，在优化过程中，参数更容易被压缩到零。这种稀疏性可以用于特征选择，将不重要的特征对应的参数置为零，从而减少模型的复杂度。
  • L2正则化：不会使参数变为零，而是将参数的值缩小到接近零。L2正则化的导数是连续的，在优化过程中，参数会逐渐趋近于零，但很难完全为零。
• 参数分布
  • L1正则化：由于其对参数的绝对值进行惩罚，会使得参数的分布更加集中在零附近，部分参数为零，其他参数也相对较小。
  • L2正则化：对参数的平方进行惩罚，会使得参数更加平滑地分布，避免参数出现过大的值。

优化求解难度

• L1正则化：由于L1正则化项在参数为零时不可导，使得优化问题变得非光滑，不能直接使用传统的基于梯度的优化算法（如梯度下降法）进行求解。通常需要使用专门的算法，如坐标下降法、近端梯度法等。
• L2正则化：L2正则化项是可导的，优化问题是一个光滑的凸优化问题，可以使用传统的基于梯度的优化算法进行求解，求解过程相对简单。

应用场景

• L1正则化：适用于需要进行特征选择的场景，当数据集中包含大量的特征，但只有部分特征是真正重要的时，L1正则化可以帮助筛选出这些重要特征，减少模型的复杂度。例如，在基因数据分析、文本分类等领域，特征数量可能非常庞大，使用L1正则化可以有效降低特征维度。
• L2正则化：适用于需要防止过拟合，同时保留所有特征的场景。当数据集中的特征都可能对模型的预测有一定的贡献时，L2正则化可以通过缩小参数的值来降低模型的复杂度，提高模型的泛化能力。例如，在图像识别、语音识别等领域，通常会使用L2正则化来优化模型。

过拟合是指模型在训练数据上表现良好，但在未见过的测试数据上表现不佳，这通常是因为模型过于复杂，学习到了训练数据中的噪声和细节。L2正则化（Ridge正则化）可以有效缓解过拟合问题：

从模型复杂度角度

• 限制参数大小：L2正则化是在原目标函数（如均方误差损失函数）的基础上添加参数的平方和作为正则化项。以线性回归为例，原目标函数为 $J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$，加入L2正则化后的目标函数变为 $J_{L2}(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$，其中 $\lambda$ 是正则化参数，${\theta }_j$ 是模型的参数。在训练过程中，为了最小化这个新的目标函数，模型会尝试同时降低原损失和参数平方和。这就使得参数 $\theta$ 的取值不能过大，避免模型过于复杂。因为复杂的模型往往需要较大的参数值来拟合训练数据中的噪声和细节，而L2正则化限制了参数大小，从而使模型变得更简单，减少了过拟合的风险。
• 降低模型方差：在统计学中，模型的误差可以分解为偏差（Bias）和方差（Variance）。过拟合的模型通常具有较高的方差，即对训练数据的微小变化非常敏感。L2正则化通过限制参数大小，使得模型对训练数据中的噪声和异常值不那么敏感，从而降低了模型的方差。模型变得更加稳定，在面对新的数据时，能够更好地泛化，减少预测误差。

从梯度更新角度

• 调整梯度方向和大小：在使用梯度下降等优化算法更新参数时，L2正则化会对梯度产生影响。对加入L2正则化后的目标函数求关于参数 (\theta_j) 的梯度，原损失部分的梯度加上正则化项的梯度。正则化项 (\frac{\lambda}{2m}\sum_{j = 1}^{n}\theta_j2) 关于 (\theta_j) 的梯度为 (\frac{\lambda}{m}\theta_j)。在每次参数更新时，这个额外的梯度会使得参数的更新方向发生改变，并且在参数值较大时，更新的幅度也会受到限制。例如，当某个参数 (\theta_j) 较大时，其梯度中的正则化项 (\frac{\lambda}{m}\theta_j) 也较大，会在更新时对该参数进行较大程度的调整，使其向零的方向靠近。这样可以避免参数在训练过程中过度增长，防止模型过拟合。
• 平滑参数更新过程：L2正则化使得参数的更新更加平滑。在没有正则化的情况下，模型可能会因为训练数据中的噪声而出现参数的剧烈波动。而L2正则化通过对参数平方和的惩罚，使得参数的更新受到一定的约束，不会出现过大的跳跃。这有助于模型在训练过程中更加稳定地收敛，避免陷入局部最优解，从而提高模型的泛化能力。

从特征选择和模型稳定性角度

• 均衡特征影响：L2正则化会对所有的参数进行惩罚，使得每个特征对模型的贡献相对均衡。在没有正则化的情况下，某些特征可能会因为其数值较大或者与目标变量的相关性较强，而在模型中占据主导地位。这可能导致模型过度依赖这些特征，对其他特征的信息利用不足，从而增加过拟合的风险。L2正则化通过限制参数大小，使得每个特征都能在模型中发挥一定的作用，提高了模型的稳定性和泛化能力。
• 增强模型鲁棒性：由于L2正则化使得模型的参数更加稳定，对输入数据的微小变化不那么敏感，因此模型具有更强的鲁棒性。在实际应用中，数据可能会受到各种噪声和干扰的影响，L2正则化可以帮助模型更好地应对这些不确定性，减少过拟合的可能性。例如，在图像识别任务中，图像可能会受到光照、噪声等因素的影响，使用L2正则化的模型能够更好地适应这些变化，提高识别的准确率。
  均值主要衡量的是一组数据的集中趋势，即数据围绕哪个数值进行分布, 方差主要衡量的是一组数据的离散程度或波动程度。它反映了数据点相对于均值的分散情况。

12 BatchNormalization中的可学习参数

批归一化（Batch Normalization，简称BN）是深度学习中一种常用的技术，可学习参数主要是缩放因子 $\gamma$ 和偏移因子 $\beta$，下面详细介绍它们的获取方式：

批归一化的基本原理回顾

在神经网络的训练过程中，批归一化通常应用在每一层的线性变换和非线性激活函数之间。对于输入的一批数据 $x^{(1)},x^{(2)},\cdots ,x^{(m)}$（$m$ 为这批数据的样本数量），批归一化的操作步骤如下：

1. 计算这批数据的均值 ${\mu }_B$：
   • ${\mu }_B=\frac{1}{m}{\sum }_{i=1}^m{x}^{(i)}$
2. 计算这批数据的方差 ${\sigma }_B^2$：
   • ${\sigma }_B^2=\frac{1}{m}{\sum }_{i=1}^m(x^{(i)}-{\mu }_B{)}^2$
3. 对数据进行标准化处理：
   • ${\hat{x}}^{(i)}=\frac{x^{(i)}-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$，其中 $ϵ$ 是一个很小的正数，用于防止分母为零。
4. 引入可学习参数进行缩放和偏移：
   • $y^{(i)}=\gamma {\hat{x}}^{(i)}+\beta$

这里的 $\gamma$ 和 $\beta$ 就是批归一化层的可学习参数，$\gamma$ 用于缩放，$\beta$ 用于偏移，它们的作用是让模型能够学习到适合自己的归一化后的数据分布。

在训练开始之前，需要对可学习参数 $\gamma$ 和 $\beta$ 进行初始化。通常的初始化方式如下：

• 缩放因子 $\gamma$：初始化为全 1 的向量。因为初始时我们希望归一化后的数据不进行缩放，保持标准化后的分布。
• 偏移因子 $\beta$：初始化为全 0 的向量。这意味着初始时不进行偏移操作。

BN本质因为深层神经网络在做非线性变换前的激活输入值随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因

BN的本质是对于每个隐层神经元，把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布，使得非线性变换函数的输入值落入对输入比较敏感的区域，以此避免梯度消失问题。

因为梯度能保持比较大的状态，所以对神经网络的参数调整效率比较高，也就是说收敛地快，经过BN后，目前大部分Activation的值落入非线性函数的线性区内，其对应的导数远离导数饱和区，这样来加速训练收敛过程。变换后某个神经元的激活x形成了均值为0，方差为1的正态分布，目的是把值往后续要进行的非线性变换的线性区拉动，增大导数值，增强反向传播信息流动性，加快训练收敛速度。但是这样会导致网络表达能力下降

如何缓解过拟合问题

过拟合是指模型在训练数据上表现良好，但在未见过的测试数据上表现不佳的现象，通常是因为模型过于复杂，学习到了训练数据中的噪声和细节。以下从数据、模型和训练策略三个方面为你介绍缓解过拟合问题的方法：

数据层面

• 增加数据量
  • 收集更多数据：尽可能收集更多与问题相关的数据，以增加训练数据的多样性和规模。例如，在图像识别任务中，可以通过网络爬虫、与数据供应商合作等方式获取更多的图像数据。
  • 数据增强：对已有的数据进行变换和扩充，生成新的训练样本。在图像领域，可以进行翻转、旋转、缩放、裁剪、添加噪声等操作；在文本领域，可以进行同义词替换、句子重组等操作。
• 数据清洗
  • 去除噪声数据：检查训练数据中是否存在错误标注、异常值等噪声数据，并将其去除。例如，在手写数字识别任务中，如果某些图像存在明显的污渍或干扰，可能会影响模型的学习，需要将这些图像剔除。
  • 处理缺失值：对于数据中的缺失值，可以采用删除、填充（如均值填充、中位数填充）等方法进行处理。

模型层面

• 简化模型结构
  • 减少模型参数：对于神经网络模型，可以减少网络的层数、神经元的数量等。例如，在设计卷积神经网络时，适当减少卷积层和全连接层的数量，或者降低每层的神经元个数。
  • 使用简单模型：如果复杂模型容易过拟合，可以尝试使用更简单的模型。例如，对于一些线性可分的问题，使用线性回归或逻辑回归模型可能比深度神经网络更合适。
• 正则化方法
  • L1和L2正则化：在损失函数中添加正则化项，限制模型参数的大小。L1正则化会使部分参数变为零，具有特征选择的作用；L2正则化会使参数的值缩小，但不会使其变为零。例如，在线性回归模型中加入L2正则化项，目标函数变为 (J(\theta)=\frac{1}{2m}\sum_{i = 1}^{{m}(h_{\theta}(x}{(i)}) - y^{(i)})2+\frac{\lambda}{2m}\sum_{j = 1}^{n}\theta_j2)，其中 (\lambda) 是正则化参数。
  • Dropout：在训练过程中，随机“丢弃”一部分神经元，使得模型不能过度依赖某些特定的神经元，从而增强模型的泛化能力。例如，在神经网络的某一层中，设置Dropout概率为0.5，意味着在每次训练时，该层的每个神经元有50%的概率被暂时忽略。

训练策略层面

• 早停策略
  • 在训练过程中，将数据集划分为训练集和验证集。随着训练的进行，定期在验证集上评估模型的性能。当验证集上的性能不再提升（如验证集损失开始上升）时，停止训练，选择此时的模型作为最终模型。
• 集成学习
  • Bagging：从原始数据集中有放回地抽样，生成多个子集，每个子集训练一个模型，最后将这些模型的预测结果进行综合（如投票、平均等）。例如，随机森林就是基于Bagging思想的集成学习方法，它由多个决策树组成。
  • Boosting：通过迭代训练多个弱分类器，每个弱分类器都在前一个弱分类器的基础上进行改进，最终将这些弱分类器组合成一个强分类器。常见的Boosting算法有AdaBoost、Gradient Boosting等。

Dropout的介绍

Dropout是深度学习中一种简单而有效的正则化技术，由 Geoffrey Hinton 等人在 2012 年提出，能有效缓解过拟合问题，提升模型的泛化能力。以下从原理、实现方式、作用机制和优缺点几个方面为你详细介绍：

原理

Dropout的核心思想是在神经网络的训练过程中，随机“丢弃”（设置为 0）一部分神经元，使得模型不能过度依赖某些特定的神经元，从而迫使模型学习到更具鲁棒性和泛化能力的特征表示。具体来说，在每次前向传播时，每个神经元都有一个固定的概率 (p) 被丢弃，这个概率 (p) 是一个超参数，通常取值为 0.2 - 0.5。在测试阶段，所有神经元都会参与计算，但为了保证输出的期望值与训练阶段一致，每个神经元的输出需要乘以 (1 - p)。

实现方式

以下是在不同深度学习框架中实现 Dropout 的示例：

PyTorch

import torch
import torch.nn as nn

# 定义一个包含 Dropout 层的简单神经网络
class SimpleNet(nn.Module):
    def __init__(self):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(10, 20)
        self.dropout = nn.Dropout(p=0.5)  # 设置 Dropout 概率为 0.5
        self.fc2 = nn.Linear(20, 1)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.dropout(x)
        x = self.fc2(x)
        return x

model = SimpleNet()
input_data = torch.randn(1, 10)
output = model(input_data)

TensorFlow/Keras

import tensorflow as tf
from tensorflow.keras import layers

# 定义一个包含 Dropout 层的简单神经网络
model = tf.keras.Sequential([
    layers.Dense(20, activation='relu', input_shape=(10,)),
    layers.Dropout(0.5),  # 设置 Dropout 概率为 0.5
    layers.Dense(1)
])

input_data = tf.random.normal([1, 10])
output = model(input_data)

作用机制

• 减少神经元之间的共适应：在没有 Dropout 的情况下，神经网络中的神经元可能会相互适应，形成特定的依赖关系，导致模型对训练数据过拟合。Dropout 通过随机丢弃神经元，打破了这种共适应关系，使得每个神经元都需要学习到更具通用性的特征，而不是依赖于其他特定神经元的输出。
• 模型平均：从另一个角度看，Dropout 相当于在每次训练时都随机生成一个子网络，整个训练过程可以看作是对多个不同子网络的训练。在测试阶段，这些子网络的预测结果被平均起来，相当于进行了一种模型平均，从而提高了模型的泛化能力。

优点

• 有效缓解过拟合：大量实验表明，Dropout 能够显著减少模型在训练数据上的过拟合现象，提高模型在测试数据上的性能。
• 简单易实现：Dropout 的实现非常简单，只需要在神经网络中添加一个 Dropout 层即可，不需要对模型结构进行复杂的修改。
• 计算效率高：Dropout 不会增加模型的训练时间和计算复杂度，反而由于减少了过拟合，可能会加快模型的收敛速度。

缺点

• 需要调整超参数：Dropout 概率 (p) 是一个超参数，需要通过实验来选择合适的值。不同的数据集和模型结构可能需要不同的 Dropout 概率，这增加了模型调优的难度。
• 训练和测试阶段处理方式不同：Dropout 在训练和测试阶段的处理方式有所不同，需要额外的代码来实现这种差异，增加了代码的复杂度。

13 DPO训练策略

DPO（Direct Preference Optimization）即直接偏好优化算法，是一种用于微调大语言模型的无奖励模型的方法，它为解决基于人类反馈的强化学习（RLHF）中存在的一些问题提供了新思路。下面为你详细介绍其原理。

背景知识：理解RLHF与问题

在传统的基于人类反馈的强化学习（RLHF）流程中，通常分为三个步骤：

1. 监督微调（SFT）：使用有标签的数据对预训练模型进行有监督的训练。
2. 奖励模型训练（RM）：收集人类对模型不同输出的偏好数据，训练一个奖励模型来评估生成结果的好坏。
3. 基于强化学习的微调：利用奖励模型作为环境反馈，使用强化学习算法（如PPO）对模型进行进一步微调。

不过，RLHF存在一些局限性，比如奖励模型训练需要大量人力标注数据，且奖励模型本身可能存在不准确的情况，还会引入额外的训练开销和不稳定性。

DPO算法原理

核心思想

DPO算法的核心思想是直接优化模型，使其输出更符合人类的偏好，而无需训练一个显式的奖励模型。它通过最大化模型生成的更受偏好输出和较不受偏好输出之间的对数概率差异来实现这一目标。

数学原理

假设我们有一组人类偏好数据，对于每个输入 $x$，有两个输出 $y_w$（更受偏好的输出）和 $y_l$（较不受偏好的输出）。模型 $p_{\theta }(y|x)$ 表示在输入 $x$ 下生成输出 $y$ 的概率。

DPO算法的目标是最大化以下目标函数：
$
J_{DPO}(\theta)=\mathbb{E}{(x,y_w,y_l)\sim D}\left[\log\left(\frac{p{\theta}(y_w|x)}{p_{\theta}(y_l|x)}\right)-\alpha \cdot \left(D_{KL}(p_{\theta}(\cdot|x)||p_{\pi}(\cdot|x))\right)\right]
$
其中：

• ${\mathbb{E}}_{(x,y_w,y_l)\sim D}$ 表示对所有偏好数据的期望。
• $\log \left(\frac{p_{\theta }(y_w|x)}{p_{\theta }(y_l|x)}\right)$ 衡量了模型生成更受偏好输出 $y_w$ 和较不受偏好输出 $y_l$ 的对数概率差异，最大化这个差异可以让模型更倾向于生成人类偏好的输出。
• $\alpha$ 是一个超参数，用于控制正则化的强度。
• $D_{KL}(p_{\theta }(\cdot |x)||p_{\pi }(\cdot |x))$ 是模型 $p_{\theta }$ 和参考模型 $p_{\pi }$ 之间的KL散度，作为正则化项，用于防止模型过度偏离参考模型（通常是监督微调后的模型），保证模型在优化过程中的稳定性。

算法步骤

1. 数据收集：收集人类对模型不同输出的偏好数据，即对于每个输入 $x$，标记出更受偏好的输出 $y_w$ 和较不受偏好的输出 $y_l$。
2. 初始化模型：通常使用经过监督微调（SFT）后的模型作为初始模型 $p_{\theta }$。
3. 目标函数优化：使用随机梯度下降（SGD）或其变种（如Adam）等优化算法来最大化上述目标函数 $J_{DPO}(\theta )$，不断更新模型的参数 $\theta$。
4. 模型评估：在训练过程中，定期使用验证集评估模型的性能，根据评估结果调整超参数（如 $\alpha$），直到模型收敛或达到预设的训练轮数。

优势

• 简化流程：无需训练额外的奖励模型，减少了人力标注成本和训练开销。
• 提高稳定性：避免了奖励模型不准确带来的问题，使得模型微调过程更加稳定。
• 高效性：可以更直接地优化模型以符合人类偏好，在一定程度上提高了训练效率。

14 GPT和Bert的架构和参数量

GPT（Generative Pretrained Transformer）和BERT（Bidirectional Encoder Representations from Transformers）都是基于Transformer架构的预训练模型，但在结构设计和参数量方面存在一定差异，以下为你详细介绍：

结构对比

整体架构基础

GPT和BERT都以Transformer架构为基础。Transformer是一种基于注意力机制的深度学习模型，主要由编码器（Encoder）和解码器（Decoder）组成。编码器负责对输入序列进行特征提取和表示学习，解码器则根据编码器的输出生成目标序列。

GPT的结构

• 仅使用解码器：GPT系列模型只使用了Transformer的解码器部分。解码器由多个相同的解码层堆叠而成，每个解码层包含多头自注意力机制（Masked Multi - Head Self - Attention）和前馈神经网络（Feed - Forward Network）。
• 单向语言模型：GPT采用单向的自注意力机制，在进行自注意力计算时，每个位置只能关注到其之前的位置，这使得它非常适合用于生成式任务，如文本生成、对话系统等。在生成文本时，模型从左到右依次生成每个词，根据之前生成的词来预测下一个词。

BERT的结构

• 仅使用编码器：BERT只使用了Transformer的编码器部分。编码器由多个相同的编码层堆叠而成，每个编码层包含多头自注意力机制（Multi - Head Self - Attention）和前馈神经网络。
• 双向语言模型：BERT采用双向的自注意力机制，每个位置可以关注到输入序列中的所有位置，能够充分利用上下文信息。这使得它在理解文本的语义和语境方面表现出色，适合用于各种自然语言处理的理解任务，如文本分类、命名实体识别、问答系统等。

参数量对比

GPT系列

• GPT - 1：参数量约为1.17亿。它是GPT系列的第一个模型，通过在大规模文本数据上进行无监督的预训练，学习到了丰富的语言知识。
• GPT - 2：参数量有多个版本，最小的版本参数量约为1.24亿，最大的版本参数量达到15亿。GPT - 2在生成文本的质量和多样性上有了显著提升。
• GPT - 3：具有多种不同参数量的版本，最小的版本参数量为1.25亿，而最大的版本参数量高达1750亿。巨大的参数量使得GPT - 3在语言理解和生成能力上达到了一个新的高度，能够完成各种复杂的自然语言处理任务。
• GPT - 4：OpenAI并未公开其具体参数量，但从其强大的性能表现来看，参数量可能比GPT - 3更大。

BERT系列

• BERT - Base：参数量约为1.1亿，包含12层编码器，768个隐藏单元，12个注意力头。
• BERT - Large：参数量约为3.4亿，包含24层编码器，1024个隐藏单元，16个注意力头。与BERT - Base相比，BERT - Large在模型复杂度和性能上都有了进一步提升，在多个自然语言处理任务上取得了更好的效果。

15 FlashAttention

Flash Attention

背景与核心目标

在Transformer架构里，标准注意力机制的计算复杂度高、内存占用大，尤其是处理长序列数据时，效率问题更为突出。Flash Attention就是为解决这些问题而生，它能显著提升注意力计算的速度，同时降低内存消耗。

原理

• 分块策略：把查询矩阵 (Q)、键矩阵 (K) 和值矩阵 (V) 划分成多个小块。在计算注意力时，无需一次性将整个 (QK^T) 矩阵存于内存，而是分块计算部分注意力分数。例如，将 (Q) 分成 (m) 个查询块 (Q_1,Q_2,\cdots,Q_m)，(K) 和 (V) 分别分成 (n) 个键块 (K_1,K_2,\cdots,K_n) 和值块 (V_1,V_2,\cdots,V_n)。
• 重排序策略：在计算每个查询块 (Q_i) 与键块 (K_j) 的注意力分数时，采用特殊的重排序方式，减少内存读写次数。同时，在计算softmax操作时也采用分块方式，避免一次性处理整个注意力分数矩阵。

优势

• 内存高效：分块计算极大减少了内存占用，处理长序列时可避免内存不足问题。
• 计算高效：重排序和分块计算减少了内存访问次数与计算量，在GPU等硬件上计算速度快。

应用场景

广泛应用于各类基于Transformer架构的模型，如语言模型、图像模型等，能加速模型训练与推理过程。

Flash Attention 2

对Flash Attention的改进

Flash Attention 2是Flash Attention的升级版，在多个方面有显著优化。

• 内存访问优化：进一步优化了内存访问模式，更充分利用硬件的内存层次结构，减少了内存带宽的需求。它通过更精细的分块和数据布局策略，降低了数据在不同存储层次（如全局内存、共享内存、寄存器）之间的传输开销。
• 计算并行度提升：对计算过程进行了更深度的并行优化，更好地发挥了GPU等硬件的并行计算能力。通过调整线程块和线程的分配方式，使得更多的计算任务可以同时进行，提高了整体计算效率。

性能提升

• 速度更快：相比Flash Attention，Flash Attention 2在相同的硬件条件下能实现更快的计算速度。例如，在处理长序列数据时，计算时间大幅缩短，加速比更为明显。
• 内存占用更低：进一步减少了内存占用，使得在有限的硬件资源下可以处理更长的序列或更大的批量数据。这对于训练和部署大规模的Transformer模型非常重要。

代码与兼容性

• 易用性增强：提供了更简洁易用的代码接口，方便开发者集成到现有的深度学习项目中。许多深度学习框架（如PyTorch）可以方便地调用Flash Attention 2进行加速。
• 兼容性好：与多种硬件平台和深度学习框架具有良好的兼容性，能够在不同的计算环境中发挥作用。

其他的高效注意力计算：
Memory Efficient Attention（内存高效注意力机制）是为了解决传统注意力机制在处理长序列数据时内存占用过大问题而提出的一系列技术。下面从背景、常见方法和优势几个方面进行介绍：

Sparse Attention

• 原理：传统注意力机制中每个查询向量会关注所有的键向量，而稀疏注意力机制限制每个查询向量只关注部分键向量。例如，采用局部注意力（每个查询只关注其附近的键）、扩张注意力（每隔一定间隔关注键）等稀疏模式，减少不必要的计算和内存占用。
• 优势：计算复杂度较低，能有效处理长序列，在一些任务中可取得与全注意力机制相近的性能。

Linformer

• 原理：对键（(K)）和值（(V)）矩阵进行线性投影，将序列长度从 (n) 降低到 (k)（(k\ll n)）。引入投影矩阵 (E) 和 (F)，使 (K’ = KE) 和 (V’ = VF)，从而将注意力计算的复杂度从 (O(n^{2}d)) 降低到 (O(nkd))。
• 优势：减少了计算和内存开销，在处理长序列时能保持较好的性能。

Performer

• 原理：基于核方法和随机特征映射，用近似的核函数代替传统点积注意力中的softmax操作。通过随机特征将输入映射到低维空间，在低维空间中高效计算注意力，计算复杂度从 (O(n^{2}d)) 降低到 (O(nd^{2}))。
• 优势：能在不损失太多性能的前提下，大幅减少计算复杂度和内存占用，可处理非常长的序列。

16 混合精度训练

FP16（半精度浮点数）量化训练是一种通过将模型参数和计算过程从FP32（单精度浮点数）转换为FP16来加速深度学习模型训练的技术。以下将从原理、具体策略以及可能面临的问题和解决办法几个方面详细介绍FP16量化训练的策略。

原理

FP32使用32位来表示一个浮点数，能提供较高的数值精度，但会占用较多的内存和计算资源。而FP16只使用16位，内存占用仅为FP32的一半，并且在支持FP16计算的硬件（如NVIDIA GPU）上，计算速度更快。不过，FP16的数值表示范围和精度低于FP32，在训练过程中可能会出现数值下溢或上溢的问题。

具体策略

混合精度训练

• 原理：结合FP32和FP16进行训练。在大部分计算（如矩阵乘法）中使用FP16以减少内存占用和提高计算速度，而在一些对精度要求较高的操作（如梯度累加）中使用FP32以保证模型的稳定性和收敛性。
• 实现步骤
  • 参数副本：维护两份模型参数，一份FP16参数用于前向和反向传播计算，另一份FP32参数作为主参数用于存储高精度的参数值。
  • 前向传播：使用FP16参数进行前向传播计算，得到预测结果和损失值。
  • 反向传播：计算FP16参数的梯度，然后将梯度转换为FP32并累加到FP32主参数的梯度上。
  • 参数更新：根据FP32主参数的梯度更新FP32主参数，再将更新后的FP32主参数复制回FP16参数。

在PyTorch中，可以使用torch.cuda.amp模块来实现混合精度训练，示例代码如下：

import torch
import torch.nn as nn
import torch.optim as optim
from torch.cuda.amp import GradScaler, autocast

# 定义模型、损失函数和优化器
model = nn.Linear(10, 1).cuda()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 创建梯度缩放器
scaler = GradScaler()

# 模拟输入数据
inputs = torch.randn(32, 10).cuda()
labels = torch.randn(32, 1).cuda()

# 训练循环
for epoch in range(10):
    optimizer.zero_grad()
    # 开启自动混合精度上下文
    with autocast():
        outputs = model(inputs)
        loss = criterion(outputs, labels)
    # 缩放损失并反向传播
    scaler.scale(loss).backward()
    # 更新参数
    scaler.step(optimizer)
    scaler.update()
    print(f'Epoch {epoch + 1}, Loss: {loss.item()}')

梯度缩放（Gradient Scaling）

• 原理：由于FP16的数值范围较小，梯度可能会因为数值下溢而变为零，导致模型无法正常更新。梯度缩放通过将损失值乘以一个缩放因子，使得梯度在反向传播过程中被放大，避免数值下溢。在更新参数之前，再将梯度除以相同的缩放因子，恢复梯度的原始值。
• 动态调整缩放因子：为了避免梯度上溢，通常采用动态调整缩放因子的方法。如果在反向传播过程中检测到梯度上溢（如出现NaN或Inf），则降低缩放因子；如果连续多个步骤没有出现梯度上溢，则增加缩放因子。

权重初始化

• 合适的初始化方法：选择合适的权重初始化方法可以减少FP16量化训练过程中的数值不稳定问题。例如，使用Xavier初始化或He初始化方法，确保模型参数在训练开始时具有合适的数值范围。

可能面临的问题和解决办法

数值下溢和上溢

• 表现：梯度变为零（下溢）或梯度值变得非常大（上溢），导致模型无法正常训练。
• 解决办法：采用梯度缩放、动态调整缩放因子以及混合精度训练等策略来缓解数值下溢和上溢问题。

模型精度下降

• 表现：与FP32训练相比，FP16量化训练后的模型在测试集上的性能可能会有所下降。
• 解决办法：在混合精度训练中，梯度缩放是一项关键技术，主要用于解决FP16（半精度浮点数）数值范围较小，在反向传播过程中梯度容易出现下溢问题。以下详细介绍梯度缩放的过程：

梯度下溢问题背景

FP16 相较于 FP32（单精度浮点数），其表示的数值范围更小。在深度学习训练的反向传播过程中，计算得到的梯度可能非常小，当使用 FP16 进行存储和计算时，这些小梯度可能会因为超出 FP16 能表示的最小数值而被舍入为零，导致梯度信息丢失，模型无法正常更新参数。

梯度缩放的基本流程

1. 初始化缩放因子

在训练开始前，需要初始化一个缩放因子（scale factor），通常这个值会设置得比较大，例如 2^16 。这个缩放因子用于在反向传播前放大损失值，从而使计算得到的梯度也相应放大，避免梯度下溢。

2. 前向传播

使用 FP16 参数进行前向传播计算。在这个过程中，模型接收输入数据，经过一系列的计算得到预测结果，然后根据预测结果和真实标签计算损失值。由于使用的是 FP16 进行计算，此时的计算速度更快，内存占用也更少。

3. 梯度缩放

将计算得到的损失值乘以缩放因子，即 scaled_loss = loss * scale_factor。然后使用缩放后的损失值进行反向传播计算梯度。这样，梯度也会被相应地放大，处于 FP16 能够表示的数值范围内，减少了梯度下溢的风险。

4. 反向传播

对缩放后的损失值进行反向传播，计算模型参数的梯度。此时得到的梯度是经过缩放后的梯度。

5. 梯度检查

在更新模型参数之前，需要检查梯度是否出现上溢（例如梯度值变为 NaN 或 Inf）。如果出现上溢，说明缩放因子设置得过大，需要降低缩放因子；如果连续多个步骤都没有出现上溢，则可以适当增加缩放因子，以充分利用 FP16 的数值范围。

6. 梯度还原

如果梯度没有出现上溢，在更新模型参数之前，需要将缩放后的梯度除以缩放因子，还原为原始的梯度值并转化为fp32，即 original_grad = scaled_grad / scale_factor。

7. 参数更新

使用还原后的梯度更新模型的 FP32 主参数（在混合精度训练中，通常会维护一份 FP32 的主参数用于存储高精度的参数值）。然后将更新后的 FP32 主参数复制回 FP16 参数，用于下一次的前向传播。

17 batch_size对模型训练有什么影响？应该如何设置

batch_size对模型训练的影响

1. 训练速度

• 小batch_size：每次训练使用的数据量较少，模型参数更新频繁。在CPU或GPU上，每次计算的开销相对较小，但频繁的参数更新会带来额外的计算和内存管理开销，例如频繁的梯度计算和参数更新操作，这可能会增加训练的总时间。而且小batch_size在并行计算方面的效率较低，不能充分利用GPU的并行计算能力。
• 大batch_size：一次处理更多的数据，能够更好地利用GPU的并行计算能力，减少了参数更新的频率，降低了额外的开销，从而提高训练速度。然而，如果batch_size过大，可能会导致GPU内存不足，无法将数据一次性加载到GPU中，从而需要更多的时间来处理数据。

2. 模型性能

• 小batch_size：由于每次迭代使用的数据量少，梯度估计的方差较大，这意味着每次更新的方向可能会有较大的波动。这种波动有时可以帮助模型跳出局部最优解，使得模型在某些情况下可能更快地收敛到全局最优解。但同时，这种不稳定性也可能导致训练过程中损失函数值出现较大的震荡，模型的训练过程不够平滑。
• 大batch_size：梯度估计更加稳定，因为它综合了更多数据的信息。这使得模型在训练过程中更加平滑，损失函数的下降趋势更加稳定。但大batch_size可能会陷入局部最优解，因为它的更新方向相对保守，缺乏足够的随机性来跳出局部最优。

3. 泛化能力

• 小batch_size：相当于在每次更新参数时引入了更多的噪声，这种噪声可以看作是一种正则化手段，有助于模型学习到更具泛化性的特征。因为模型需要适应不同小批量数据中的变化，从而减少了对训练数据的过拟合，提高了模型在测试数据上的性能。
• 大batch_size：模型可能会对训练数据产生过拟合，因为它在更新参数时更多地依赖于整体数据的统计信息，而忽略了数据中的局部特征和变化。这可能导致模型在训练数据上表现良好，但在测试数据上的性能下降。

4. GPU内存占用

• 小batch_size：每次加载到GPU中的数据量较少，因此对GPU内存的需求较低。这使得在GPU内存有限的情况下，也可以进行模型训练。
• 大batch_size：需要将更多的数据加载到GPU中，对GPU内存的需求较高。如果batch_size设置得过大，超过了GPU的内存上限，会导致内存溢出错误，训练过程无法正常进行。

如何设置batch_size以避免跑到GPU内存上限

1. 初始试探

• 从一个较小的batch_size开始尝试，例如2、4、8等。观察训练过程中GPU的内存使用情况和训练速度。如果GPU内存使用远低于上限，且训练速度较慢，可以逐步增加batch_size。
• 可以使用深度学习框架提供的工具来监控GPU内存使用情况，如PyTorch中的torch.cuda.memory_allocated()和torch.cuda.max_memory_allocated()函数。

2. 考虑模型复杂度

• 模型越复杂，参数越多，需要的GPU内存就越大。对于复杂的模型，如具有大量层和神经元的深度神经网络，应该选择较小的batch_size。
• 例如，对于一个具有数十亿参数的大型语言模型，可能需要将batch_size设置为1或2，以避免GPU内存溢出。

3. 数据维度和类型

• 数据的维度和类型也会影响GPU内存的使用。高分辨率的图像数据、长序列的文本数据等会占用更多的内存。
• 如果数据维度较大，可以适当减小batch_size。同时，使用低精度的数据类型（如FP16）可以减少内存占用，从而允许使用更大的batch_size。

4. 经验法则

• 在实际应用中，有一些经验法则可以参考。对于常见的图像分类任务，batch_size通常设置为32、64或128；对于自然语言处理任务，batch_size可能会根据数据集和模型的不同而有所变化，一般在16 - 64之间。

5. 动态调整

• 在训练过程中，可以根据GPU内存的使用情况动态调整batch_size。如果发现GPU内存使用接近上限，可以适当减小batch_size；如果GPU内存有较大的空闲，可以尝试增加batch_size以提高训练速度。

18 Pre-Norm 和Post-Norm的区别

四 AIGC

1采样方式

1） DDPM

其中

这里的训练和推理过程都是无控制的，即无法控制其输出图片是什么，如果要添加控制，要在U-net中额外加入控制条件。

2） DDIM

DDIM将求一个概率分布求成了一个确切的值，即将DDPM中的采样过程中的、sigma_t 设为0，即其去除了随机性，同一个初始噪声得到的结果是相同的，但ddpm时随机的。
而且将采样的连续步长改为了一个可以不连续的步长，但是必须是严格单调递增的。即去除了DDPM中的隐马尔可夫假设


不再根据贝叶斯公式求取去噪过程，而是直接假设

3） Improved DDPM

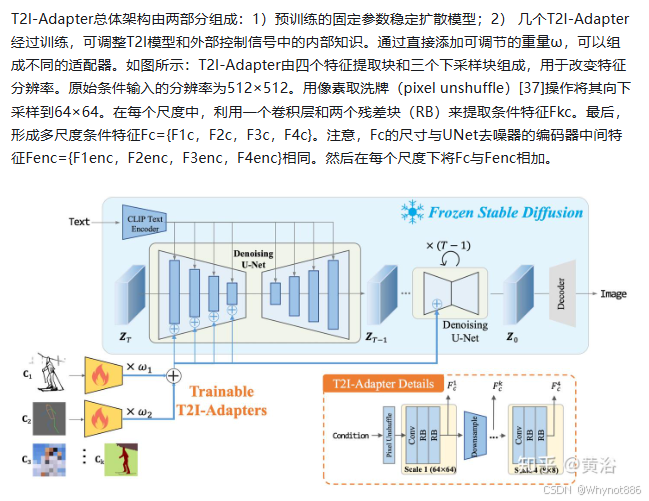
3 T2I-Adapter

4 ControlNet

整体架构：

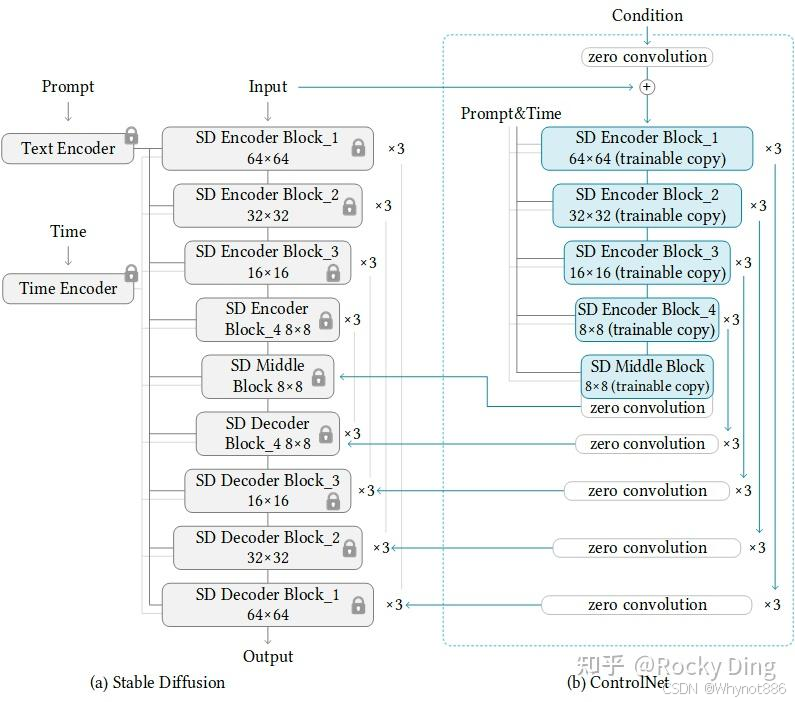
除了右边的controlnet多了一个condition输入，其余的输入都是一样的
conditions编码过程：

CFG权重重新分配


总之只要一个模块他的输入不是全0，那他的导数就不一定为0

5 SD 1 2 3 XL区别

6 扩散模型为什么要使用高斯噪声，能否使用别的分布代替？

在扩散模型中添加高斯噪声主要有以下几个原因：

数学性质优良

• 易于处理：高斯分布具有简单而明确的数学形式，其概率密度函数由均值和方差完全确定。在扩散模型的正向过程中，向数据中添加高斯噪声可以通过简单的线性组合来实现，即 $x_t=\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}$ ，其中 ${ϵ}_{t-1}$ 是从高斯分布中采样得到的噪声。这种简单的数学形式使得在理论分析和实际计算中都非常方便，便于模型的训练和优化。
• 中心极限定理：根据中心极限定理，大量独立同分布的随机变量之和近似服从高斯分布。在扩散过程中，多次添加小的噪声可以看作是多个随机变量的累加，因此最终的噪声分布近似为高斯分布。这为在扩散模型中使用高斯噪声提供了理论依据，使得模型能够更好地模拟自然数据的分布特性。

符合数据分布特性

• 数据平滑与去结构化：高斯噪声具有平滑的特性，能够逐步破坏数据的原始结构，将数据从其原始分布逐渐转换为一个简单的、各向同性的高斯分布。在图像数据中，这意味着将图像的像素值逐渐打乱，使其失去原有的纹理、形状和语义信息，最终变成一团噪声。这种去结构化的过程使得模型能够更好地学习数据的潜在分布，从而在反向去噪过程中生成高质量的样本。
• 模拟自然噪声：在现实世界中，许多自然现象和信号都受到高斯噪声的影响。例如，图像在采集、传输和处理过程中会受到高斯噪声的干扰。因此，在扩散模型中添加高斯噪声可以更好地模拟这些自然过程，使模型生成的样本更加真实和自然。

便于模型训练和反向采样

• 反向过程的可解性：由于高斯分布的数学性质，在扩散模型的反向去噪过程中，可以通过简单的数学推导得到从噪声中恢复原始数据的方法。例如，通过预测添加的高斯噪声，并根据已知的噪声时间表和扩散过程的参数，可以逐步反向推导得到原始数据的估计值。这种可解性使得模型的训练和反向采样过程更加高效和稳定。
• 训练稳定性：高斯噪声的引入有助于提高模型的训练稳定性。在训练过程中，模型需要学习如何从带噪声的数据中恢复出原始数据，高斯噪声的平稳性和可预测性使得模型能够更好地学习到数据的本质特征，避免过拟合和梯度爆炸等问题。
• 在扩散模型中，除了高斯噪声，也可以使用其他类型的噪声，但高斯噪声因其独特优势成为主流选择，以下为你介绍其他类型噪声使用的可能性及相关问题：

理论上可行的其他噪声类型

• 均匀噪声
  • 原理：均匀噪声在一个固定的区间内均匀分布，每个值出现的概率相等。在图像中添加均匀噪声时，像素值会在一定范围内随机变化。
  • 应用情况：理论上可用于扩散模型。例如在一些对图像细节要求不高、更注重整体风格和随机变化的场景中可以尝试使用。不过，由于均匀噪声的分布特性，它可能会导致图像出现块状或颗粒状的不自然效果，因为其分布不像高斯噪声那样平滑。
• 椒盐噪声
  • 原理：椒盐噪声是由图像中的随机黑白像素点组成，会在图像中随机出现黑色或白色的噪点，就像撒在图像上的椒盐一样。
  • 应用情况：在某些特殊的图像生成任务中可能有应用价值，比如模拟图像的损坏或老化效果。但椒盐噪声是一种脉冲噪声，其离散性和随机性较强，与扩散模型通常假设的平滑数据分布不太相符，会增加模型学习和去噪的难度。

使用其他噪声面临的挑战

• 数学处理复杂性：高斯噪声具有良好的数学性质，如在计算均值、方差和进行概率推导时较为简单。而其他类型的噪声可能不具备这些特性，导致在扩散模型的正向和反向过程中，数学处理变得复杂，难以进行有效的理论分析和模型优化。
• 模型训练难度：不同类型的噪声会对数据分布产生不同的影响。扩散模型通常是基于高斯噪声的假设进行设计和训练的，如果使用其他噪声，模型可能需要重新调整架构和训练策略，以适应新的噪声分布。这可能会增加模型训练的难度和时间成本，甚至可能导致模型性能下降。
• 生成效果不确定性：高斯噪声在扩散模型中的应用已经经过了大量的实验和验证，能够生成高质量、多样化的样本。而使用其他类型的噪声时，生成效果可能难以预测和控制，可能无法达到与高斯噪声相同的生成质量和稳定性。

7 文生图微调方法：

textual inverse：

首先确定一个代表你新生成物体的占位符和能用自然语言最接近地描述这个物体的初始化词
计算这个占位符在tokenizer词表中的id，然后记录下来，之后将这个占位符的embedding用初始化词的embedding替换掉用作初始化，然后微调整个embedding空间。最后将原本embedding中除了占位符之外token的embedding还原，只留下占位符的embedding

DreamBooth

1 新物体的文本提示不再是一个词表中没有的词而是一个词表中的罕见词，
使用经常使用的词会使模型忘掉之前词的意思，而使用过长的随即词会使词被分为多个token
2
权重默认为1，就是两个损失函数平均相加

8 Classifier Guidance 和 Classifier-Free Guidance

CFG的输出是无条件噪声+权重乘以（有条件噪声减去无条件噪声的差）

9 DIT (diffusion transformer)

模型仍然使用一个LDM的架构，先将图片通过VQVAE转换到隐状态，然后再进行去噪

1）加噪方式：训练过程中的加噪方式不再是一个DDPM中的线性加噪，而是一个cos加噪，即Improved DDPM

2） 模型架构选取了四种模型架构，实验发现adaLN-zero是最优的效果，四种方案和模型架构：

3）AdaLN-zero Block 就是对于原始的LN中的均值和标准差的可学习参数删掉，让这个均值和方差由控制条件经过MLP之后得到

4）时间编码器或嵌入器实现方式：先使用正弦余弦位置编码，然后经过MLP映射维度

5）类别嵌入器只使用一个embedding

6）decoder：

10 Imagen系列

1）imagen1

模型架构

text encoder

动态CFG阈值

融合机制

高效Unet

Drawbench

2）Imagen2 没有论文 只是一些功能上的扩展

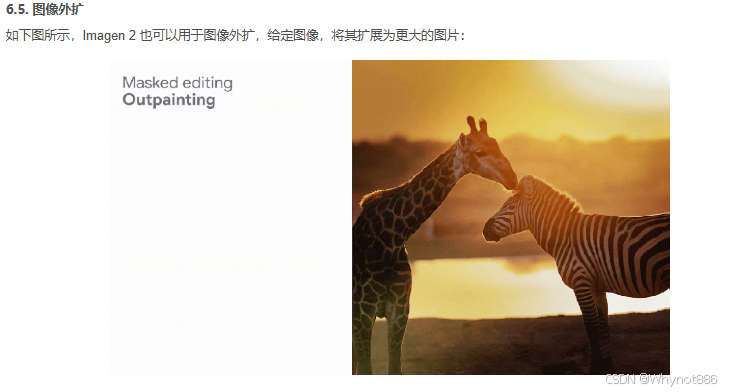
11 Dall-E 系列

1）dalle1

模型架构

包括一个vqvae 将图像转化为token，使用BPE将文本转化为token，将文本token和图像token拼接起来放到GPT内部，以文本作为前缀，自回归的预测下一个图片token

训练

推理

2）DallE2

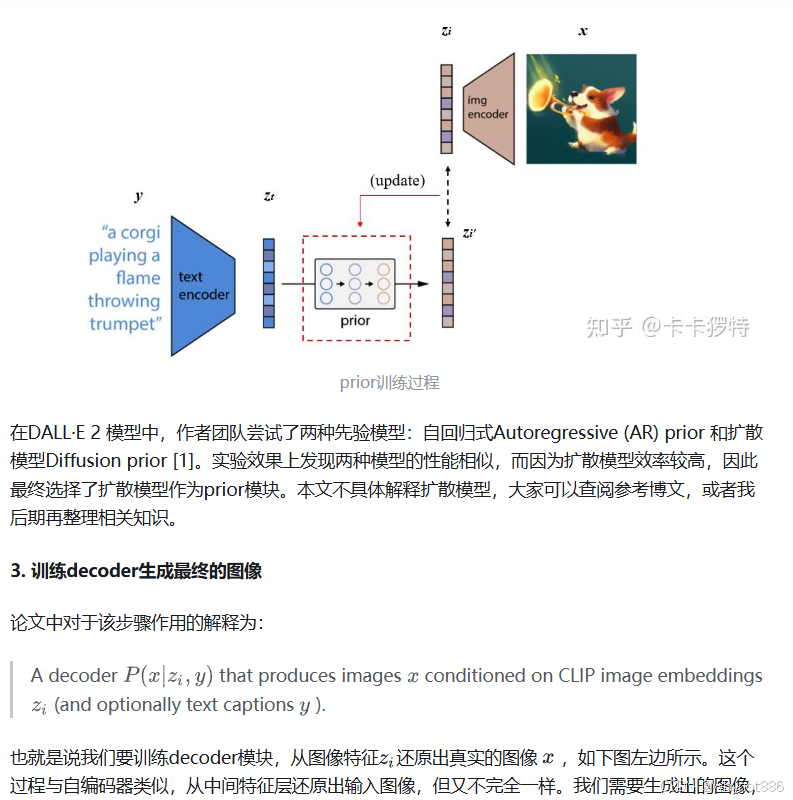
12 VAE GAN DM的区别

13 使用CLIP编码特征的优缺点

在文生图任务中使用CLIP（Contrastive Language - Image Pretraining）编码特征有其独特的优势，但也存在一些缺点，以下为你详细分析：

优点

强大的跨模态理解能力

• 语义关联：CLIP经过大规模的图像 - 文本对数据训练，能够学习到图像和文本之间的语义关联。在文生图任务中，它可以准确地将输入的文本描述映射到对应的视觉概念上。例如，当输入“一只奔跑的白色小狗”这样的文本时，CLIP能够理解其中“小狗”“奔跑”“白色”等语义信息，并将其转化为适合图像生成模型使用的特征，使得生成的图像更符合文本描述。
• 泛化性：由于训练数据的多样性，CLIP具有很强的泛化能力。它可以处理各种不同领域、不同风格的文本描述，无论是常见的自然场景、动物，还是抽象的概念、艺术风格等，都能较好地编码出有意义的特征，为图像生成提供丰富的语义指导。

提高生成图像的质量和一致性

• 细节捕捉：CLIP能够捕捉文本中的细微语义差别，帮助图像生成模型生成更具细节和准确性的图像。比如，对于“一个穿着红色连衣裙、戴着珍珠项链的年轻女孩”的描述，CLIP可以将这些细节信息编码到特征中，使生成的图像能够呈现出女孩的穿着、配饰等细节。
• 一致性保证：在生成图像的过程中，使用CLIP编码的特征可以确保生成的图像与输入文本在语义上保持一致。避免出现生成的图像与文本描述不符的情况，提高了图像生成的可靠性和质量。

易于集成和使用

• 开放性：CLIP是开源的，并且有成熟的预训练模型可供使用。这使得开发者可以方便地将其集成到各种文生图模型中，无需从头开始训练跨模态模型，节省了大量的时间和计算资源。
• 灵活性：CLIP可以作为一个独立的模块，与不同的图像生成架构（如扩散模型、GAN等）相结合。它可以在不同的训练和推理阶段发挥作用，为图像生成系统提供了很大的灵活性。

缺点

计算资源消耗

• 训练和推理成本：CLIP模型本身规模较大，在进行特征编码时需要消耗一定的计算资源和时间。尤其是在处理大规模数据集或进行实时图像生成时，计算成本可能会成为一个限制因素。
• 硬件要求：为了保证编码效率，需要配备较高性能的GPU等硬件设备。这对于一些资源有限的用户或场景来说，可能会增加使用门槛。

语义理解的局限性

• 复杂语义处理：尽管CLIP具有较强的语义理解能力，但在处理一些复杂的、模糊的或具有歧义的文本描述时，可能会出现理解不准确的情况。例如，对于一些隐喻、双关语或需要特定文化背景知识的文本，CLIP可能无法完全理解其深层含义，从而影响生成图像的质量。
• 缺乏上下文推理：CLIP在编码文本特征时，主要基于当前输入的文本，缺乏对上下文的深度推理能力。在一些需要根据上下文信息来生成图像的场景中，可能无法提供足够准确的特征指导。

生成多样性的限制

• 特征偏差：由于CLIP的训练数据和方式的影响，它可能会存在一定的特征偏差。这可能导致在使用CLIP编码特征进行文生图时，生成的图像在风格、视角等方面存在一定的局限性，缺乏足够的多样性。

最大token个数限制了输入文本序列的长度

五 RAG 检索增强生成

1 数据准备

1. 数据收集与清洗

• ‌多源数据采集‌：从PDF、数据库、网页等多渠道获取非结构化数据，需进行格式标准化与隐私脱敏（如医疗领域患者信息处理）‌:ml-citation{ref=“3,4” data=“citationList”}
• ‌多模态处理‌：对图文混合文档采用端到端编码技术（如ViRAG），避免传统OCR解析导致的信息丢失‌:ml-citation{ref=“4,6” data=“citationList”}

2. 分块策略优化

• ‌动态切分方法‌：
  • 基础分块：按固定字符长度划分（512-1024 tokens）‌
  • 语义分块：结合句法分析识别段落边界‌
  • 递归分块：构建树状层级结构处理长文档
• ‌质量验证‌：通过实体覆盖率（≥85%）评估分块信息完整性

3. 向量化与索引构建

• ‌嵌入模型选择‌：
  • 单模态：BERT/GPT系列文本嵌入‌
  • 多模态：集成CLIP/ViT实现图文联合编码
• ‌混合索引架构‌：

  索引类型	技术实现	典型场景
  向量索引	FAISS/Milvus	语义相似度匹配‌
  关键词倒排索引	Elasticsearch	精确术语检索‌
  知识图谱	Neo4j	实体关系推理

4.优化方法

元数据增强

• 添加创作者、时间戳、数据来源等标签，提升检索精准度（如音乐BGM标注节奏、流派）‌
• 支持文档版本管理与增量更新（Delta Index技术）

质量评估体系

• ‌分块质量‌：实体覆盖率检测与语义连贯性分析
• ‌向量表征‌：余弦相似度方差计算（目标值≥0.3）
• ‌检索效率‌：百万级数据延迟控制（目标<200ms）

5. 典型挑战与解决方案

挑战类型	解决方案	技术支撑
图文数据对齐	ViRAG技术实现联合编码	CLIP模型
长文档信息割裂	递归分块+层级注意力机制	Transformer-XL‌:ml-citation
实时更新需求	增量索引构建（Delta Index）	Pinecone‌:ml-citation

2 检索过程

RAG（Retrieval-Augmented Generation）检索是将用户输入与向量数据库中的知识进行匹配，为后续的文本生成提供相关信息的重要过程。以下为你详细介绍其各个步骤：

1. 用户输入接收与解析

• 接收输入：用户提出问题、给出指令或提供一段文本，这是整个RAG检索流程的起点。输入可以是自然语言问题，如“珠穆朗玛峰的高度是多少？”，也可以是特定领域的查询请求。
• 输入解析：系统会对用户输入进行初步处理，包括去除噪声，如特殊字符、多余空格等，统一大小写，以及进行分词操作。对于中文输入，可能会使用专业的分词工具，将句子拆分成单个的词语；对于英文输入，会将句子按空格分割成单词。

2. 输入编码

• 选择编码器：选用合适的文本编码器将解析后的用户输入转化为向量表示。常见的编码器包括基于Transformer架构的预训练语言模型，如BERT、Sentence - BERT、Dense Passage Retrieval（DPR）编码器等。这些模型在大规模文本数据上进行了预训练，能够学习到文本的语义信息，将文本映射到低维向量空间中。
• 编码操作：将处理后的用户输入送入选定的编码器，模型会根据自身的参数和结构，对输入进行计算，最终输出一个固定维度的向量。这个向量代表了用户输入的语义特征，可用于后续在向量数据库中的相似度计算。

3. 向量数据库检索

• 相似度计算：将编码后的用户输入向量与向量数据库中的所有向量（或部分经过筛选的向量）进行相似度计算。常用的相似度度量方法有余弦相似度、欧几里得距离、曼哈顿距离等。余弦相似度衡量的是两个向量的方向相似性，值越接近1表示越相似；欧几里得距离衡量的是两个向量在空间中的实际距离，值越小表示越相似。
• 检索策略：向量数据库通常采用一些索引结构和算法来加速检索过程，如KD树、球树、局部敏感哈希（LSH）、可导航小世界图（NSW）、乘积量化（PQ）等。这些方法可以减少不必要的相似度计算，提高检索效率。在检索时，根据相似度得分对数据库中的向量进行排序，找出与用户输入向量最相似的若干个向量。

4. 关联文本获取

• 数据映射：向量数据库中的每个向量通常都与原始的文本数据（如文档、段落、句子等）存在关联关系。在检索到相似向量后，根据这种关联关系，从数据库中提取对应的原始文本内容。
• 文本筛选：对获取到的相关文本进行初步筛选，去除一些质量较差、不相关或重复的文本。例如，如果检索结果中包含一些广告、无关的注释等内容，可以将其过滤掉。

5. 文本重排序与筛选

• 综合评估：对筛选后的文本进行进一步的重排序和筛选。除了考虑向量相似度得分外，还可以结合其他因素进行综合评估，如文本的权威性、时效性、相关性等。例如，在新闻检索中，优先选择权威媒体发布的、最新的报道。
• 排序算法：可以使用一些机器学习模型或启发式算法对文本进行排序。例如，训练一个二分类模型，判断文本与用户输入的相关性；或者使用基于规则的方法，根据文本的特征（如标题、关键词出现频率等）进行排序。

6. 结果输出与传递

• 输出结果：将经过重排序和筛选后的文本作为最终的检索结果输出。结果可以是一个或多个文本片段，也可以是完整的文档。
• 传递给生成模块：将检索结果传递给后续的文本生成模块。生成模块会结合这些相关信息和自身的语言生成能力，生成回答用户问题或满足用户需求的文本内容。例如，在问答系统中，根据检索到的关于珠穆朗玛峰高度的信息，生成一个清晰、准确的回答。

3 RAG出现幻觉

4 RAG的微调

5 数据集

1. 2WikiMultiHopQA

2WikiMultiHopQA 数据集侧重于多跳推理问题，所谓多跳推理，是指回答一个问题需要从多个不同的文档或信息片段中收集和整合信息，就像在知识图谱上进行多次“跳跃”来找到最终答案。该数据集基于维基百科文章构建，旨在模拟现实世界中需要复杂推理的问答场景。

• 问题生成：数据集中的问题是人工精心设计的，这些问题需要模型进行多步推理才能找到答案。例如，问题可能涉及到多个实体之间的关系，需要在不同的维基百科页面中查找相关信息并进行整合。
• 文档选择：为每个问题选择相关的维基百科文档，这些文档包含了回答问题所需的信息。文档的选择确保了问题的答案可以通过对这些文档的推理和分析得到。
• 答案标注：对每个问题标注了正确答案，同时还提供了支持答案的证据文档和推理步骤，方便模型训练和评估。

2. Musique

MuSiQue数据集是一个多跳问答数据集，通过组合来自其他单跳数据集（如SQuAD、T-REx、Natural Questions、MLQA和Zero Shot RE）的问题创建。数据集包含两个配置：answerable和full，每个配置都有训练集和验证集。特征包括id、paragraphs、question、question_decomposition、answer和answerable。使用该数据集时需要注意避免信息泄露，特别是当使用其种子单跳数据集时。

3. HotpotQA

HotpotQA是英文维基百科上收集的问答数据集，包含大约 113K 的众包问题，这些问题被构建为需要两篇维基百科文章的介绍段落来回答。数据集中的每个问题都带有两个黄金段落，以及这些段落中的句子列表，众包工作者认为这些句子是回答问题所必需的支持事实。
HotpotQA 具有多种推理策略，包括涉及问题中缺失实体的问题、交集问题（什么满足属性 A 和属性 B？）以及比较问题，其中两个实体通过共同属性进行比较等。在少文档干扰器设置中，QA 模型有十个段落，其中保证找到黄金段落；在开放域 fullwiki 设置中，模型只给出问题和整个维基百科。模型根据它们的答案准确性和可解释性进行评估，其中前者被测量为具有精确匹配 (EM) 和 unigram F1 的预测和黄金答案之间的重叠，后者关注预测的支持事实句子与人类注释的匹配程度（支持事实EM/F1)。

4. CQA

ConcurrentQA是一个文本多跳问答基准，要求跨多个数据分布（如维基百科和电子邮件数据）进行并发检索。该数据集由斯坦福大学和FAIR的研究人员构建，遵循了HotpotQA的数据收集过程和模式。该基准可用于研究检索中的泛化能力以及跨多个隐私范围（如公共维基百科文档和私人电子邮件）进行推理时的隐私问题

6 Baselines

Efficient RAG（高效检索增强生成）是为了提升RAG（Retrieval-Augmented Generation）系统效率而提出的一系列方法和技术，旨在解决传统RAG在计算资源、时间成本等方面的问题，以下从优化思路、关键技术、应用场景和优势几方面进行介绍：

优化思路
传统RAG系统在检索和生成过程中可能面临计算量大、速度慢等问题。Efficient RAG主要从检索模块和生成模块两个方面进行优化，以提高系统的整体效率，同时尽可能保证生成结果的质量。

关键技术

检索模块优化

• 轻量级检索器：设计更简单、计算量更小的检索模型来替代复杂的大型检索器。例如，使用基于哈希的近似最近邻搜索算法（如局部敏感哈希LSH），可以在保证一定检索精度的前提下，显著降低检索的时间复杂度。
• 预过滤和索引优化：对知识库进行预过滤，只保留与常见查询相关的文档，减少检索空间。同时，优化索引结构，如采用分层索引或多粒度索引，提高检索的速度。例如，在大规模文本知识库中，先通过粗粒度的索引快速定位到可能包含相关信息的文档子集，再在子集中进行细粒度的检索。
• 多阶段检索：采用多阶段检索策略，先使用快速但精度较低的方法进行初步检索，筛选出少量候选文档，然后再使用更精确但计算量较大的方法对候选文档进行精细检索，从而在保证检索准确性的同时提高效率。

生成模块优化

• 知识蒸馏：将大型、复杂的生成模型的知识蒸馏到小型、轻量级的模型中。通过让小型模型学习大型模型的输出分布，在减少模型参数和计算量的同时，保持相近的生成性能。
• 自适应生成：根据检索到的信息的数量和质量，动态调整生成过程。例如，当检索到的信息足够丰富时，采用更简洁的生成策略；当信息不足时，通过更多的推理和泛化来生成内容，避免不必要的计算。
• 增量生成：对于较长的生成任务，采用增量生成的方式，逐块生成内容，同时可以根据已生成的部分和检索到的信息实时调整后续的生成，提高生成效率。

应用场景

• 实时问答系统：在需要快速响应用户问题的场景中，如智能客服、实时搜索等，Efficient RAG可以在短时间内完成检索和生成过程，提供及时准确的回答。
• 资源受限环境：在移动设备、嵌入式系统等计算资源有限的环境中，Efficient RAG可以通过减少计算量和内存占用，使RAG系统能够正常运行。
• 大规模数据处理：当面对大规模的知识库和大量的用户查询时，Efficient RAG能够有效提高系统的处理能力和效率，满足实际应用的需求。

优势

• 降低成本：通过减少计算资源的消耗，降低了系统的运行成本，包括硬件成本、能源成本等。
• 提高响应速度：能够在更短的时间内完成检索和生成任务，提高了系统的实时性和用户体验。
• 增强可扩展性：在处理大规模数据和高并发查询时表现更优，使得RAG系统能够更好地适应不同规模和复杂度的应用场景。

Auto RAG（自动化检索增强生成）是在RAG（Retrieval-Augmented Generation）基础上发展而来，强调检索和生成过程的自动化，以下从基本概念、实现方式、优势和应用场景几个方面为你详细介绍：

AutoRAG

传统的RAG系统在检索和生成过程中，可能需要人工进行一些参数调整、示例选择等操作。而Auto RAG旨在通过自动化的方式，让系统能够自动完成从查询输入到结果生成的整个流程，减少人工干预，提高效率和准确性。

• 自动化检索
  • 自适应检索策略：系统能够根据输入查询的特点，自动选择合适的检索策略。例如，对于简单的查询，采用快速的近似检索方法；对于复杂的查询，使用更精确但计算量较大的检索算法。
  • 动态索引更新：能够自动监测知识库的变化，实时更新索引结构，确保检索的准确性和效率。当有新的文档加入知识库或旧文档被更新时，系统可以自动对索引进行调整。
• 自动化生成
  • 自动提示生成：根据检索到的信息，自动生成合适的提示信息，引导生成模块生成更准确、更符合需求的内容。例如，在生成回答时，自动组织检索到的关键信息作为提示，让生成模块围绕这些信息进行回答。
  • 模型自动选择和调优：系统可以根据任务的类型和数据的特点，自动选择最合适的生成模型，并对模型的参数进行自动调优。例如，对于不同领域的问答任务，自动选择在该领域表现较好的生成模型，并通过自动化的超参数搜索方法调整模型的参数。

SelfRAG

SelfRAG是一种在RAG（Retrieval - Augmented Generation）基础上发展起来的创新方法，它强调系统的自我优化和自我反馈机制，以提升整体性能。以下从核心概念、工作机制、优势和应用场景几个方面详细介绍：

传统的RAG系统通常由检索模块和生成模块组成，而SelfRAG在这基础上增加了自我监督和自我改进的能力。它能够在运行过程中不断评估自身的输出质量，根据评估结果自动调整检索策略和生成方式，从而实现系统性能的持续提升。
工作机制

• 自我评估：SelfRAG系统会对生成的结果进行自我评估。评估指标可以包括答案的准确性、完整性、相关性等。例如，在问答场景中，系统可以通过与已知的标准答案进行对比，或者利用一些预定义的规则和模型来判断生成的回答是否正确和有用。
• 反馈调整：根据自我评估的结果，系统会自动调整检索模块和生成模块的参数和策略。如果发现生成的答案不准确，可能是检索到的信息不够相关，系统会调整检索的相似度阈值或者更换检索算法；如果答案不够完整，可能会调整生成模块的生成策略，使其更全面地利用检索到的信息。
• 迭代优化：通过不断地进行自我评估和反馈调整，SelfRAG系统会进行迭代优化，逐步提高在各种任务上的性能。每一次的优化都会作为下一次评估和调整的基础，形成一个良性的循环。

优势

• 自适应优化：SelfRAG能够根据不同的输入和任务自动调整自身的行为，适应各种复杂的场景。无需人工手动调整参数，系统可以在运行过程中不断学习和改进，提高了系统的灵活性和适应性。
• 提高性能稳定性：通过持续的自我评估和调整，系统能够及时发现和纠正自身的错误和不足，减少因数据变化、模型偏差等因素导致的性能波动，使系统的性能更加稳定。
• 减少人工干预：在传统的RAG系统中，需要人工进行大量的参数调整和模型优化工作。而SelfRAG的自我优化机制大大减少了人工干预的需求，降低了人力成本和时间成本。

Iter-RetGen

Iter-RetGen 即迭代式检索 - 生成（Iterative Retrieval - Generation），是对传统 RAG（Retrieval - Augmented Generation）架构的一种优化与拓展，旨在通过多次迭代检索和生成过程，不断提升生成结果的质量。以下为你详细介绍：

核心概念
传统的 RAG 通常是进行一次检索操作获取相关文档，然后基于这些文档进行内容生成。而 Iter - RetGen 引入了迭代机制，在初始检索和生成之后，会根据生成的中间结果再次进行检索，获取更多补充信息，然后再次进行生成，如此反复迭代，逐步完善最终的生成结果。

工作流程

1. 初始检索：当接收到用户的查询后，系统首先利用检索模块从知识库中检索与查询相关的文档。这一过程可以采用传统的检索算法，如基于向量相似度的检索方法，获取一批初步认为相关的文档。
2. 首次生成：生成模块根据初始检索得到的文档信息，生成一个初步的回答或结果。这个结果可能并不完善，可能存在信息缺失、不准确等问题。
3. 迭代循环：
   • 重新检索：对首次生成的结果进行分析，识别出其中可能需要进一步补充信息的部分。然后，以这些信息需求为新的查询，再次使用检索模块从知识库中检索相关文档。新检索到的文档可以提供更多的细节、证据或不同角度的信息。
   • 再次生成：生成模块将新检索到的文档信息与之前的生成结果相结合，重新生成一个更完善的回答或结果。
   • 循环判断：判断是否满足迭代终止条件，如达到预设的迭代次数、生成结果的质量提升不再显著等。如果不满足终止条件，则继续进行下一轮的重新检索和再次生成。
4. 最终输出：当满足迭代终止条件时，将最终的生成结果作为系统的输出返回给用户。

优势

• 提升信息完整性：通过多次迭代检索和生成，能够不断补充新的信息，使生成的结果更加全面、完整。例如，在回答一个复杂的历史问题时，初始生成的结果可能只涵盖了主要事件，经过迭代可以补充更多的背景信息、相关人物的细节等。
• 增强结果准确性：每一次迭代都可以对之前生成的内容进行修正和完善，提高生成结果的准确性。可以根据新检索到的信息纠正之前的错误或不准确的表述。
• 适应复杂问题：对于那些需要多方面知识和深入分析的复杂问题，Iter - RetGen 能够通过迭代的方式逐步挖掘和整合相关信息，更好地应对复杂任务。

6 评价指标

RAG（Retrieval - Augmented Generation，检索增强生成）系统结合了信息检索和文本生成，其评价指标可以从检索模块、生成模块以及整体系统效果等多个维度来考量，以下是一些常见的评价指标：

1）检索模块评价指标

准确率（Precision）

• 定义：检索出的相关文档数量占检索出的所有文档数量的比例。例如，系统检索出了10篇文档，其中有6篇是与查询相关的，那么准确率就是 $6÷10=0.6$。
• 作用：衡量检索结果的相关性程度，准确率越高，说明检索出的文档中相关文档的比例越大。

召回率（Recall）

• 定义：检索出的相关文档数量占数据集中所有相关文档数量的比例。假设数据集中总共有20篇相关文档，系统检索出了6篇，那么召回率就是 $6÷20=0.3$。
• 作用：反映检索系统能够找到所有相关文档的能力，召回率越高，说明检索系统能够覆盖更多的相关文档。

F1值

• 定义：准确率和召回率的调和平均数，公式为 $F1=2\times \frac{Precision\times Recall}{Precision+Recall}$。
• 作用：综合考虑了准确率和召回率，当需要同时平衡准确率和召回率时，F1值是一个很好的评价指标。

平均精度均值（Mean Average Precision，MAP）

• 定义：对于每个查询，计算其在检索结果排序中的平均精度，然后对所有查询的平均精度求平均值。平均精度是指在检索到的相关文档位置上的准确率的平均值。
• 作用：考虑了检索结果的排序情况，更全面地评价了检索系统在多个查询上的性能。

平均倒数排名（Mean Reciprocal Rank，MRR）

定义：对于每个查询，计算其第一个相关文档在检索结果中的排名的倒数，然后对所有查询的倒数排名求平均值得到。主要用于评估检索系统在返回第一个相关结果时的效率。
计算公式：MRR = （1 / 第一个相关文档的排名）的平均值。例如，对于三个查询，第一个相关文档的排名分别为 2、3、1，则 MRR = （1/2 + 1/3 + 1/1）/3 = 11/18≈0.61。MRR 的值越高，说明检索系统越能快速地将相关文档排在前面。

命中率

命中率指的是在检索任务中，检索到的相关文档包含了标准答案所需信息的比例。简单来说，就是检索结果中能够命中正确信息的概率。

假设进行了 $N$ 次检索任务，其中有 $M$ 次检索到的文档包含了与标准答案相关的信息，则命中率（HR）的计算公式为：
$HR=\frac{M}{N}\times 100\%$

例如，在一个问答系统中，用户提出了 100 个问题，检索模块针对这些问题进行文档检索，其中有 80 次检索到的文档包含了可以用于回答问题的有效信息，那么该检索模块的命中率就是 $\frac{80}{100}\times 100\%=80\%$。

2）生成模块评价指标

BLEU（Bilingual Evaluation Understudy）

• 定义：主要用于评价机器翻译结果，但也可用于评价文本生成的质量。它通过比较生成文本和参考文本之间的n - gram（连续的n个词）匹配程度来计算得分。
• 作用：衡量生成文本与参考文本的相似度，得分越高说明生成文本与参考文本越相似。

ROUGE（Recall - Oriented Understudy for Gisting Evaluation）

• 定义：有多种变体，如ROUGE - N（N - gram匹配）、ROUGE - L（最长公共子序列匹配）等。它侧重于评价生成文本与参考文本之间的召回率。
• 作用：常用于评价文本摘要生成的质量，得分越高表示生成文本能够覆盖参考文本的信息越多。

METEOR（Metric for Evaluation of Translation with Explicit ORdering）

• 定义：综合考虑了单词语义匹配、词干匹配和词序等因素，通过计算生成文本和参考文本之间的匹配得分来评价生成质量。
• 作用：在评价文本生成时，能够更全面地考虑语义和词序信息，比单纯的n - gram匹配更具优势。

3） 整体系统评价指标

准确性（Accuracy）

• 定义：系统生成的回答正确的比例。在问答系统中，可以通过人工判断或与标准答案对比来确定回答是否正确。
• 作用：直接衡量整个RAG系统生成的回答的正确性。

连贯性（Coherence）

• 定义：生成的文本在逻辑和语义上是否连贯一致。可以通过人工评估或使用一些基于语言模型的连贯性度量方法来评价。
• 作用：确保生成的文本易于理解，逻辑清晰，符合正常的语言表达习惯。

有用性（Usefulness）

• 定义：生成的回答对用户是否有实际帮助。可以通过用户反馈或人工评估来判断。
• 作用：从用户的角度评价系统生成的回答是否能够满足他们的需求。

4）ROUGE（Recall-Oriented Understudy for Gisting Evaluation）是一种在自然语言处理领域中，用于评估自动文本摘要和机器翻译等任务中生成文本质量的常用指标。以下是关于它的详细介绍：

主要类型

• ROUGE-N
  • 含义：基于n-gram的重叠来计算得分。它统计生成文本与参考文本中共同出现的n-gram的数量。
  • 计算方式：例如ROUGE-1表示单字（unigram）的重叠情况，ROUGE-2表示双字（bigram）的重叠等。计算公式为$ROUGE-N=\frac{{\sum }_{n-gram\in ref}{\sum }_{n-gram\in sys}Coun{t}_{match}(n-gram)}{{\sum }_{n-gram\in ref}Count(n-gram)}$，其中$Coun{t}_{match}(n-gram)$是生成文本和参考文本中共同的n-gram的数量，$Count(n-gram)$是参考文本中n-gram的数量。
• ROUGE-L
  • 含义：基于最长公共子序列（Longest Common Subsequence，LCS）来计算。它考虑了生成文本和参考文本之间最长的连续子序列的匹配情况，不要求匹配的子序列在原文中是连续的，但顺序必须一致。
  • 计算方式：得分基于LCS的长度，结合召回率和准确率的计算方式，如$F_{LCS}=\frac{(1+{\beta }^2)P_{LCS}{R}_{LCS}}{P_{LCS}+{\beta }^2{R}_{LCS}}$，其中$P_{LCS}$是基于LCS的准确率，$R_{LCS}$是基于LCS的召回率，$\beta$通常取1，用于平衡准确率和召回率。
• ROUGE-W
  • 含义：是ROUGE-L的扩展，它对最长公共子序列中的元素赋予了权重，更注重较长的连续匹配序列，给长的匹配子序列更高的权重，以突出文本中较长、更有意义的片段的匹配。
  • 计算方式：在计算最长公共子序列的基础上，为每个匹配的子序列元素根据其在子序列中的位置和长度等因素分配权重，然后计算加权后的得分。
• ROUGE-S
  • 含义：基于skip-bigram的统计。Skip-bigram是指允许在两个词之间跳过一定数量的词形成的二元组。它可以捕捉文本中词与词之间的远距离依赖关系，比传统的bigram更灵活地反映文本的语义结构。
  • 计算方式：统计生成文本和参考文本中共同出现的skip-bigram的数量，并根据出现的频率等因素计算得分。

特点

• 基于召回率：ROUGE指标的设计核心是基于召回率，重点关注生成文本能够覆盖参考文本的程度，即有多少参考文本中的信息在生成文本中被体现出来。
• 多维度评估：通过不同类型的ROUGE指标，如ROUGE-N关注n-gram的精确匹配，ROUGE-L考虑最长公共子序列等，可以从多个角度评估生成文本与参考文本的相似性，更全面地反映文本生成的质量。
• 广泛应用：在自动文本摘要、机器翻译、问答系统等自然语言处理任务的评估中被广泛使用，是衡量生成文本与人工标注的参考文本之间相似度的重要工具，有助于比较不同模型或算法在文本生成任务上的性能。

局限性

• 语义理解有限：主要基于文本的表面形式进行匹配，对文本的语义理解能力相对较弱，可能无法准确判断语义相同但表达方式不同的文本的相似性。
• 参考文本依赖：评估结果高度依赖于参考文本的质量和多样性，如果参考文本存在偏差或不完整，可能会影响对生成文本质量的准确评估。
• 难以评估连贯性和流畅性：对于生成文本的连贯性、流畅性等方面的评估能力不足，主要关注文本内容的匹配，而对文本的整体质量的其他方面考虑不够全面。

5）METEOR（Metric for Evaluation of Translation with Explicit ORdering）

作为一种机器翻译评估指标，在计算方式、特点及应用等方面还有很多细节，以下是更详细的介绍：

详细计算方法

1. 标记化和对齐
   • 首先对候选翻译和参考翻译进行标记化处理，将句子分割成单词或短语等基本单元。
   • 然后通过各种匹配方式找到候选翻译和参考翻译之间的对应关系，建立对齐。
2. 匹配类型及权重
   • 精确匹配：这是最直接的匹配方式，若候选翻译中的单词与参考翻译中的单词完全相同，则记为精确匹配。精确匹配在METEOR的计算中通常占有一定的基础权重。
   • 词干匹配：利用词干提取算法，将单词还原为词干形式进行匹配。比如“compute”“computing”“computed”的词干都是“compute”。词干匹配的权重一般低于精确匹配，因为它在一定程度上允许了词汇形式的变化，但仍保持核心意义的一致。
   • 同义词匹配：借助同义词词典或知识库来确定两个单词是否为同义词。例如在英语中，“big”和“large”可视为同义词。同义词匹配的权重相对较低，因为同义词之间可能存在细微的语义差别。
   • 基于WordNet的匹配：WordNet是一种广泛使用的英语词汇语义知识库，METEOR会利用WordNet中的语义关系来寻找更复杂的语义匹配。例如，若两个单词在WordNet中属于同一语义类别或具有特定的语义关联，也会被视为一种匹配。这种匹配方式在METEOR计算中所占权重较小，但能捕捉到更深入的语义相似性。
3. 惩罚机制
   • 碎片惩罚：如果匹配的单词或短语在候选翻译中是分散的、不连续的，会根据不连续的程度给予一定的惩罚。例如，若参考翻译是“the quick brown fox”，候选翻译是“the fox quick brown”，虽然单词都匹配，但顺序混乱，会受到碎片惩罚。
   • 语法惩罚：METEOR会分析句子的语法结构，若候选翻译的语法结构与参考翻译差异较大，也会进行惩罚。比如，参考翻译是主动语态，而候选翻译错误地使用了被动语态，就可能触发语法惩罚。
4. 最终得分计算
   • 综合考虑各种匹配类型的数量和权重，以及惩罚因素，使用特定的公式计算METEOR得分。一般来说，先计算出匹配得分，然后根据惩罚项对匹配得分进行调整，最终得到一个在0到1之间的分数。具体公式为：(METEOR = \frac{(1 + \beta^2)PR}{\beta2P + R})，其中(P)是准确率，(R)是召回率，(\beta)是用于平衡准确率和召回率的参数，通常取值为3，这意味着更注重召回率。准确率和召回率的计算会考虑各种匹配情况和惩罚因素。

与其他评估指标的比较

• 与BLEU的对比
  • BLEU：侧重于计算n-gram的精确匹配率，对句子中连续的单词片段匹配较为敏感，但对语义和语法的理解相对有限，不太能处理同义词替换、词序变化等情况。
  • METEOR：更注重语义和语法层面的匹配，不仅考虑单词的表面形式，还能通过词干、同义词等匹配方式捕捉更丰富的语义信息，对词序变化等情况也有更好的适应性。
• 与ROUGE的对比
  • ROUGE：主要用于自动摘要系统的评估，侧重于计算生成的摘要与参考摘要之间的重叠单元，如n-gram、词块等。
  • METEOR：专门为机器翻译评估设计，在考虑词汇和语义匹配的基础上，还针对翻译任务中的语法、词序等特点进行了优化，更适合评估翻译文本的质量。

在不同语言对翻译评估中的表现

• 在印欧语系语言对中的表现
  • 对于英语、法语、德语等印欧语系语言之间的翻译评估，METEOR能够很好地利用这些语言丰富的词汇资源和相对规范的语法体系，通过词干提取、同义词匹配等方式准确地评估翻译质量，其评估结果与人工评估结果通常具有较高的一致性。
• 在跨语系语言对中的表现
  • 对于如中英、中日等跨语系语言对的翻译评估，METEOR也能通过合理选择和调整匹配策略及参数，较好地处理语言之间在词汇、语法和文化等方面的差异。例如，在中英翻译评估中，它可以借助中文的分词技术和英文的词汇处理方法，找到两种语言之间的语义对应关系，从而给出较为合理的评估结果。

应用案例及局限性

• 应用案例
  • 在WMT（Workshop on Machine Translation）等国际知名的机器翻译评测竞赛中，METEOR是常用的评估指标之一，用于比较不同参赛团队的机器翻译系统性能，推动了机器翻译技术的发展。
  • 许多机器翻译研究机构和企业在研发过程中，使用METEOR来评估和优化自己的翻译模型，帮助提高翻译质量。
• 局限性
  • 依赖参考翻译的质量：METEOR的评估结果高度依赖参考翻译的准确性和质量。如果参考翻译存在错误或不恰当的表达，可能会影响METEOR对候选翻译的评估。
  • 对一些语言现象处理有限：对于一些具有丰富文化内涵、隐喻、口语化等复杂语言现象的翻译，METEOR可能无法完全准确地评估其质量，因为它主要基于词汇和语法层面的匹配，对深层次的文化和语用信息处理能力有限。
  • 计算成本相对较高：与一些简单的评估指标相比，METEOR由于涉及多种匹配方式和复杂的计算过程，计算成本较高，在处理大规模数据时可能会面临效率问题。