直观理解特征值、特征向量

把矩阵看作是运动，对于运动而言，最重要的当然就是运动的速度和方向

• 特征值就是运动的速度
• 特征向量就是运动的方向

说明下，因为线性变换总是在各种基之间变来变去，所以我下面画图都会把作图所用的基和原点给画出来。

在$\vec{i}，\vec{j}$下面有个向量$\vec{v}$ ：

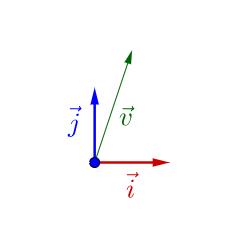
随便左乘一个矩阵$A$，图像看上去没有什么特殊的：

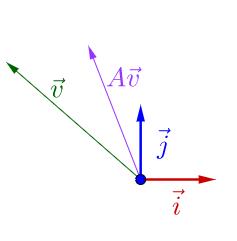
我调整下 $\vec{v}$ 的方向，图像看上去有点特殊了：

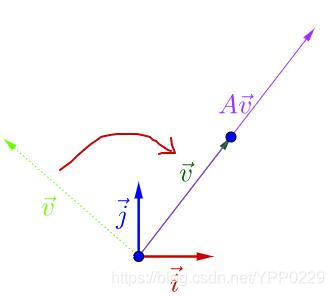
可以观察到，调整后的$\vec{v}$和$A\vec{v}$在同一根直线上，只是$A\vec{v}$的长度相对$\vec{v}$的长度变长了。

此时，我们就称$\vec{v}$是$A$的特征向量，而 $A\vec{v}$ 的长度是$\vec{v}$的长度的 $\lambda$ 倍，$\lambda$ 就是特征值。

从而，特征值与特征向量的定义式就是这样的：

其实之前的 $A$ 不止一个特征向量，还有一个特征向量：

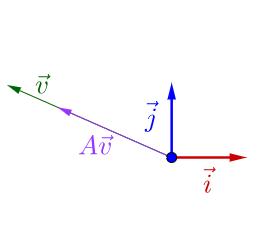
容易从 $A\vec{v}$ 相对于 $\vec{v}$ 是变长了还是缩短看出，这两个特征向量对应的特征 $\lambda$ 值，一个大于1，一个小于1。

从特征向量和特征值的定义式还可以看出，特征向量所在直线上的向量都是特征向量：

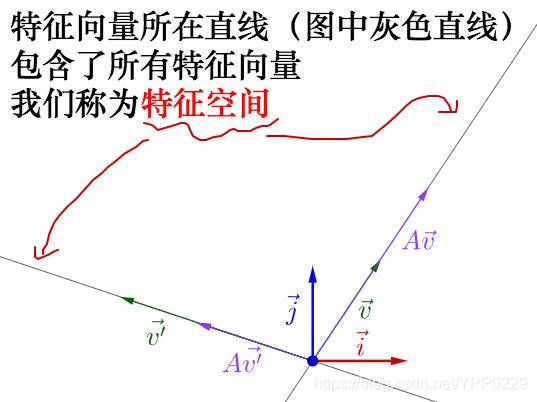
一般来说，矩阵我们可以看作某种运动，而二维向量可以看作平面上的一个点（或者说一个箭头）。对于点我们是可以观察的，但是运动我们是不能直接观察的。

就好像，跑步这个动作，我们不附加到具体的某个事物上是观察不到的，我们只能观察到：人跑步、猪跑步、老虎跑步、…，然后从中总结出跑步的特点。

所以，要观察矩阵所代表的运动，需要把它附加到向量上才观察的出来：

似乎还看不出什么。但是如果我反复运用矩阵乘法的话：

就像之前颜料混合一样，反复运用矩阵乘法，矩阵所代表的运动的最明显的特征，即速度最大的方向，就由最大特征值对应的特征向量展现了出来。

本文内容，均转载自“马同学高等数学”微信公众号，从知乎追到微信，真的受益颇多！