1. 定积分是怎么定义的？
按照现在的语言就是 ∫ a b f ( x ) d x = ∑ f ( x ) d x \int_a^bf(x)dx=\sum f(x)dx ∫abf(x)dx=∑f(x)dx，所以定积分最初是被定义成面积的。
2. 牛顿-莱布尼兹公式
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
\int_a^bf(x)dx=F(b)-F(a)
∫abf(x)dx=F(b)−F(a)
定积分可以求面积，我们已经知道了，但是用于计算定积分的最出名的牛顿-莱布尼兹公式是怎么被牛顿、莱布尼兹发现的？
牛顿搞物理研究，就是喜欢求导数。
给位移求导数得到速度，给速度求导数得到加速度。
搞数学研究也这么搞，他想给面积求下导数：
接下来，我们对面积函数
A
(
x
)
A(x)
A(x)来求导：
A
′
(
x
)
=
d
A
(
x
)
d
x
=
A
(
x
+
d
x
)
−
A
(
x
)
d
x
=
f
(
x
)
d
x
d
x
=
f
(
x
)
A'(x)=\frac{dA(x)}{dx}=\frac{A(x+dx)-A(x)}{dx}=\frac{f(x)dx}{dx}=f(x)
A′(x)=dxdA(x)=dxA(x+dx)−A(x)=dxf(x)dx=f(x)
所以牛顿得出结论，面积的导数就是曲线，曲线的原函数就是面积。
对牛顿-莱布尼兹公式，在这里给出一个直观的说明：
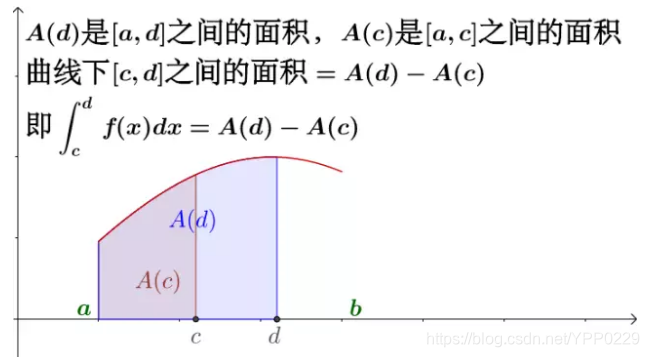
本文内容，均转载自“马同学高等数学”微信公众号，从知乎追到微信，真的受益颇多！
扫一扫
2472
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
